Презентация на тему: Дифференциал и интеграл

Лекция № 4. Тема: «Дифференциал и интеграл» Специальность: «Сестринское дело»Курс: 2Дисциплина: «Математика» Подготовила: преподаватель высшей категории Фёдорова Олеся НиколаевнаКалуга 2010 год

Функция. Предел функции Функцией называется соответствие при котором каждому значению x из некоторого множества D (DR) сопоставляется по некоторому правилу единственное число y, зависящее от xy= f(x)x – аргумент функции (независимая переменная)y – значение функции f (зависимая переменная)D – область определения функции D (f) – все значения xВсе значения y – область значений функции f , E (f)

Графиком функции называется множество точек плоскости с координатами (x; y), где x пробегает всю область определения функции fСпособы задания функцииАналитический (рекуррентный) – формулаГрафический – график функцииТабличный – таблица зависимости x и y

Рассмотрим интервал с центром в точке x0 и радиусом rОкрестностью точки x0 радиуса r называется интервал с центром в точке x0 радиуса r, (x0)Если рассматривается окрестность без самой точки x0, то она называется проколотой (x0)

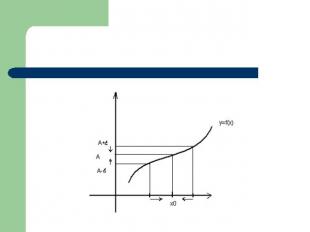
Предел функции Число A называется пределом функции f(x) в точке x0, если для любого числа , существует окрестность , такая, что выполняется неравенствоf(x)-A, для любого x из окрестности (x0)f(x)-AAf(x)A+

Теоремы о пределах Теорема о единственности предела: если предел функции существует, то он единственный (число A)Теорема о пределе суммы: если существуют пределы функций f(x) и g(x), то существует предел их суммы равный сумме пределов функций f(x) и g(x)

Теорема о пределе произведения: если существуют пределы функций f(x) и g(x), то существует предел их произведения равный произведению пределов функций f(x) и g(x)Теорема о пределе частного: если существуют пределы функций f(x) и g(x) и предел функции g(x) не равен нулю, то существует предел их частного равный частному пределов функций f(x) и g(x)

Следствия из теорем Следствие 1: постоянный множитель можно вынести за знак пределаСледствие 2: если n натуральное число, то

Следствие 3: предел многочлена равен значению многочлена в точке x0 при Следствие 4: предел дробно –рациональной функции равен значению этой функции в точке x0 при если x принадлежит области определения функции

Пример:

Производная функции и дифференциал Производная функции – это предел отношения приращения функции к приращению аргумента, когда приращения аргумента стремится к нулю

Свойства производной Теорема: производная суммы, произведения, частного вычисляются по следующим формулам:

Производная сложной функции: Пример:

Таблица производных

Дифференциал функции Нахождение производной называется дифференцированиемДифференциал – это произведение производной функции на приращение аргумента функции y = f(x)dy = f'(x)xРассмотрим функцию y = x, тогда y'= 1 dx = x dy = f'(x)dx (отношение дифференциалов)

Свойства дифференциала Дифференциал функции – это главная часть её приращенияДифференциал функции – это линейная функция приращения аргумента или касательная к графику функции геометрически dy = f'(x)dx - уравнение касательной в системе координат (dx; dy)

Вычисление дифференциала функции Пример.

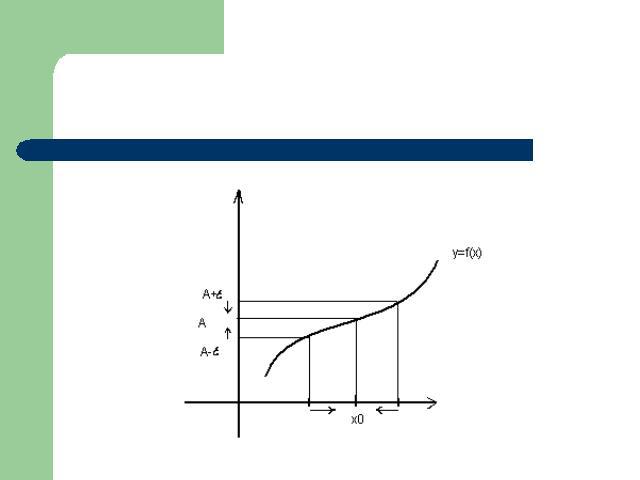
Применение дифференциала к приближенным вычислениям Для функции y=f(x) и точки x0 можно приближенно вычислить значение функции в точке x близкой к x0, если знать приращение функции y на [x0; x], то точное значение функции f(x) = y0+ y, где y0 значение функции в точке x0 Приближенные формулы основаны на замене приращения функции y её дифференциалом dyy = f(x) - y0 f(x) - y0 f '(x0) xf(x) y0+ dy y0 + f '(x0)(x – x0)

Для y = xn(x0+ x)n x0n + nx0n-1xПример:

Первообразная функции и интеграл Первообразная и неопределенный интегралСвойства неопределенного интегралаТаблица первообразныхМетоды интегрирования: непосредственное, замена переменной, интегрирование по частямОпределенный интеграл. Формула Ньютона – ЛейбницаПрименение определенного интеграла: вычисление площади фигуры, длины дуги, объема телаДифференциальные уравнения. Уравнения с разделяющимися переменными