Презентация на тему: Решение задач с помощью квадратных уравнений

Решение задач с помощью квадратных уравнений

Цели и задачи урока Научиться решению задач с помощью квадратных уравнений.Уметь хорошо решать квадратные уравнения, составлять уравнения по условию задачи, следить за речью, правильным произношением звуков, правильным ударением.

Математику уже затем учить следует, что она ум в порядок приводит

Кто это?

Тест Какое из уравнений является квадратным?а)4-3х=0; б) 5х2-2х+3=0; в) 2х4-5х2=0.2. Назовите коэффициенты a, b м свободныйчлен с в уравнении 2-5х+3х2=0.Запишите формулу дискриминанта.Установите соответствие:а)D ˃ 0 1 ) корней нетб)D = 0 2) два корняв)D ˂ 0 3) один корень

Продолжение теста 5) Вычислите дискриминант квадратного уравнения 2х2-3х-2=06) составьте уравнение решения задачи:Одна сторона прямоугольника на 5 м больше другой, а его площадь равна 84 М2 Найти стороны прямоугольника.

Ответы к тесту (б); 2) а=3, б=-5, с=2; 3) D= b2 – 4ac;4) D ˃ 0, 1 ) два корня,б)D = 0, 2) один корень,в)D ˂ 0, 3) нет корней.5) 25; 6) х(х+5)=84.

Площадь прямоугольного треугольника

Задача Площадь прямоугольного треугольника равна 180 см2 . Найти катеты этого треугольника, если один катет больше другого на 31 см .

Алгоритм решения задачи Выберем неизвестное, которое обозначим через х.По условию задачи запишем алгебраические выражения.Составим уравнение.Решим его.Анализируем, подходят ли корни по условию задачи.

Продолжение алгоритма Если мы получили ответ на вопрос задачи, то делаем проверку.Записываем ответ.ЗАПОМНИ! ПРЕЖДЕ ЧЕМ ЗАПИСАТЬ ОТВЕТ – ПРОЧИТАЙ ЕЩЁ РАЗ ВОПРОС.

Историческая справка Математика отражает развитие человеческой мысли, интеллекта. А когда люди научились решать квадратные уравнения?Необходимость решать квадратные уравнения была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков, с земляными работами военного характера, а также с развитием астрономии и математики. Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне.

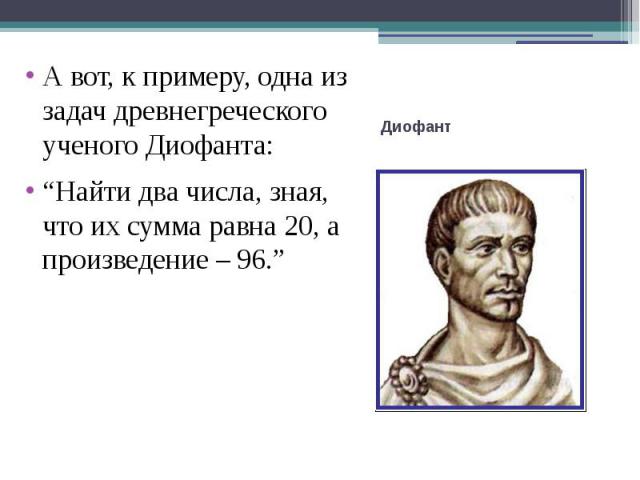
А вот, к примеру, одна из задач древнегреческого ученого Диофанта:“Найти два числа, зная, что их сумма равна 20, а произведение – 96.”

Задачи на квадратные уравнения встречаются уже в астрономическом трактате индийского математика и астронома Ариабхаты в 499 г.Багдад IX век. В алгебраическом трактате ал-Хорезми дается классификация квадратных уравнений. Например, его задача: “Квадрат и число 21 равны 10 корням. Найти корень” (подразумевается корень уравнения х2 + 21 = 10х).

В Европе впервые квадратные уравнения были изложены в “Книге абака”, написанной в 1202 г итальянским математиком Леонардо Фибоначчи. Общее правило решения квадратных уравнений было сформулировано в Европе лишь в 1544 г. М. Штифелем.

Итальянский математик Леонардо Фибоначчи

Задача на «5» Найдите катеты прямоугольного треугольника, если их сумма равна 23 см, а гипотенуза 17 см.

Задача на «4» Спортивная площадка имеет форму прямоугольника, длина которого на 5 см больше ширины, а площадь ее 1050 м2. Найдите размеры площадки.

Задача на «3» Произведение двух натуральных чисел равно 221. Найдите эти числа, если одно из них на 4 больше другого.

Ответы к задачам На «5»15см и 8см;На «4»30см и 35см;На «3»13см и 17см.

Домашнее задание Площадь прямоугольного треугольника 52 см2. Найдите катеты этого треугольника, если один катет больше другого на 5 см.2)Задача Диофанта. Найти два числа, зная, что их сумма равна 20, а произведение – 96.3)Повторить формулу, связывающую скорость, время и расстояние.