Презентация на тему: Выпуклость и вогнутость функции

Выпуклость и вогнутость функцииПрезентация к уроку по учебнику «Алгебра и начала анализа, 10-11» под редакцией Ш.А.Алимова , § 53Автор презентации Бартош Наталья Владимировна, учитель математики 587 гимназии г. Санкт-Петербурга

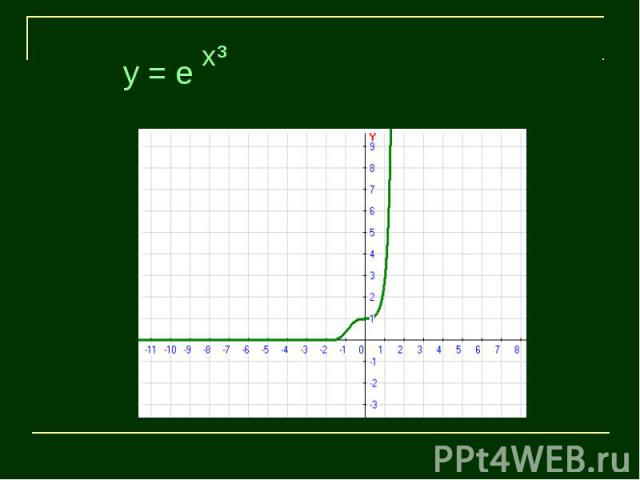
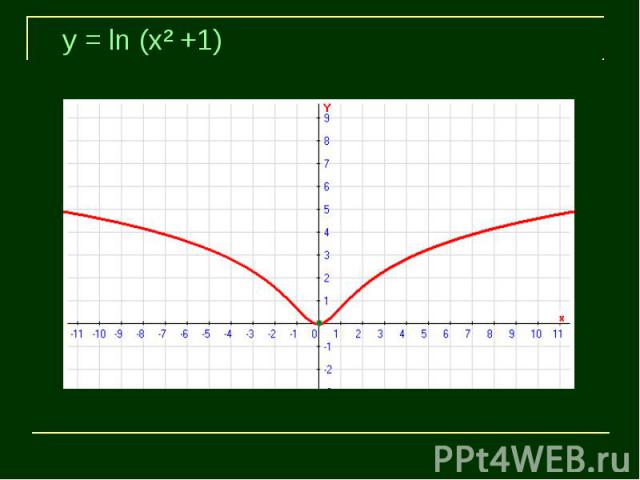
Самостоятельная работаПостроить график функцииВариант 1Вариант 2

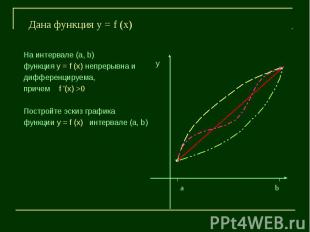
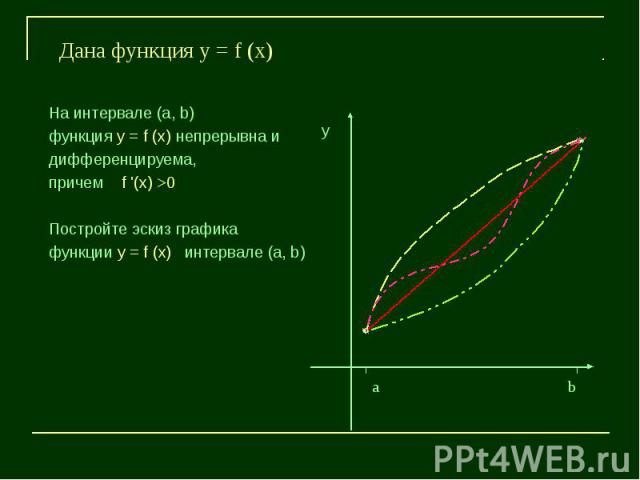
На интервале (а, b)функция у = f (x) непрерывна и дифференцируема, причем f '(x) >0Постройте эскиз графикафункции у = f (x) интервале (а, b)

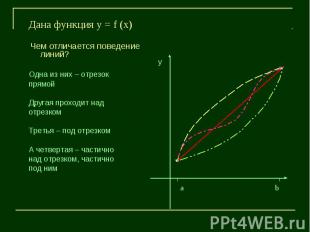
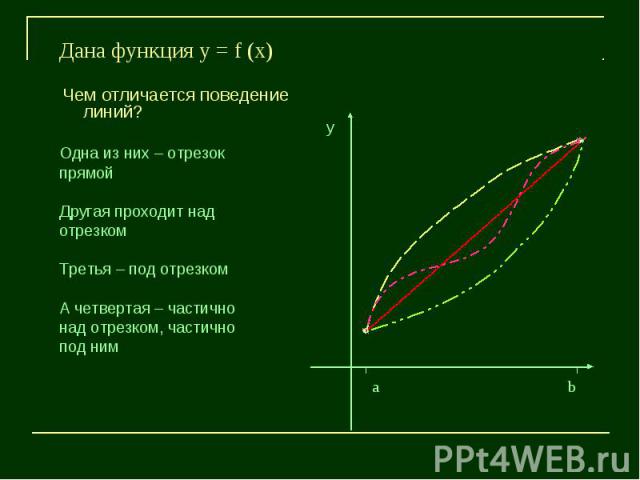
Чем отличается поведение линий?Одна из них – отрезок прямойДругая проходит над отрезкомТретья – под отрезкомА четвертая – частично над отрезком, частично под ним

В математике для обозначения такого поведения существуют специальные понятия: выпуклости и вогнутостиграфика функции

Выпуклость и вогнутость функцииГеометрический смысл второй производной

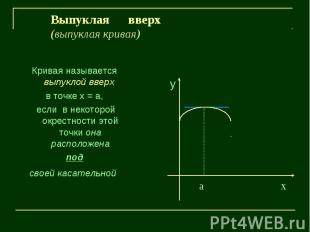
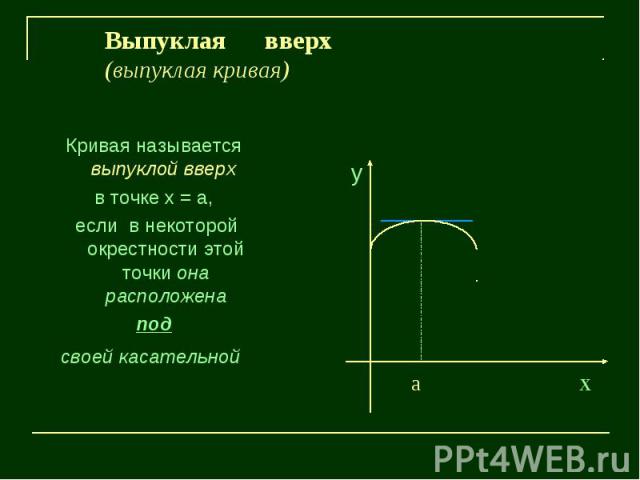
Выпуклая вверх(выпуклая кривая)Кривая называется выпуклой вверх в точке х = а, если в некоторой окрестности этой точки она расположенаподсвоей касательной

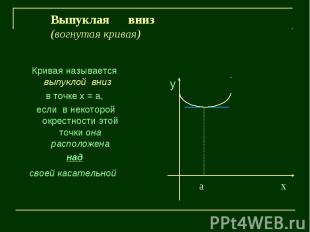
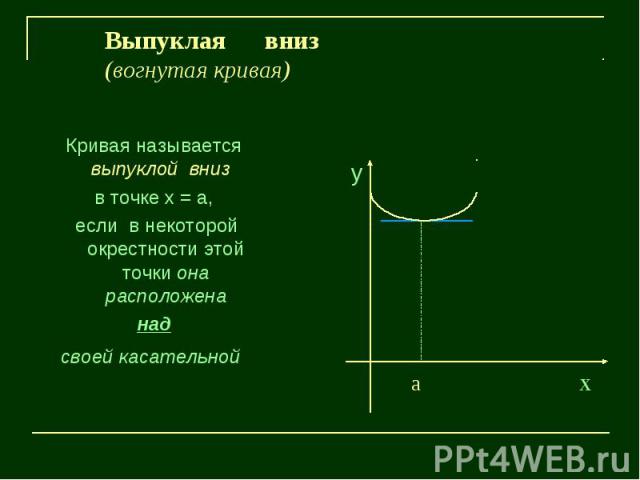
Выпуклая вниз(вогнутая кривая)Кривая называется выпуклой вниз в точке х = а, если в некоторой окрестности этой точки она расположенанадсвоей касательной

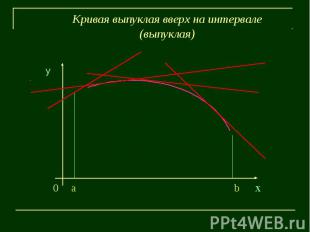
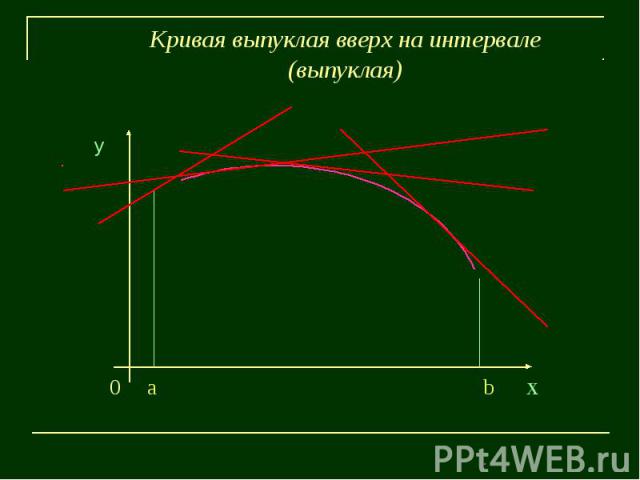
Кривая выпуклая вверх на интервале(выпуклая)у

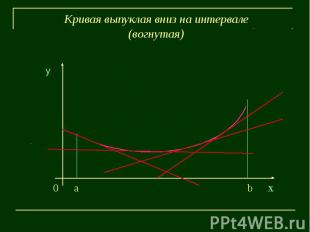
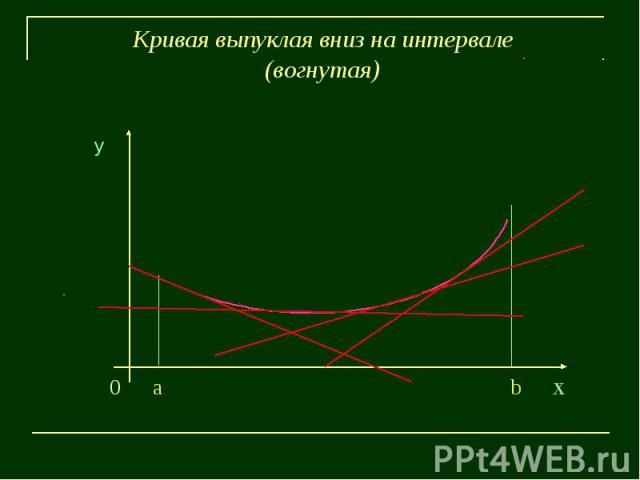
Кривая выпуклая вниз на интервале(вогнутая)у

Как найти интервалы выпуклости и вогнутости?

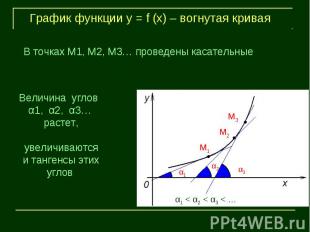
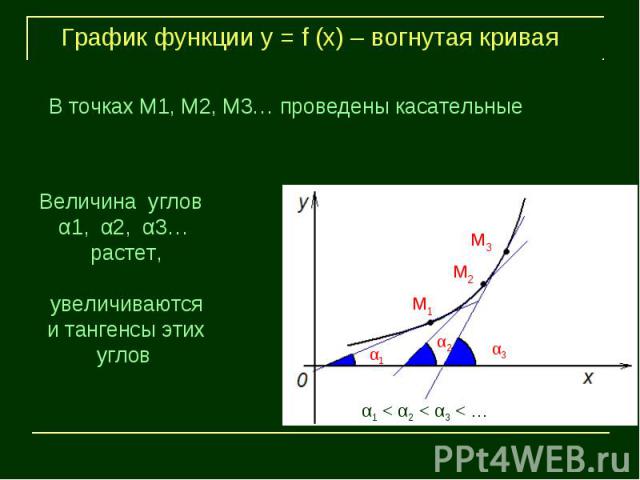
График функции у = f (х) – вогнутая криваяВ точках М1, М2, М3… проведены касательныеВеличина углов α1, α2, α3… растет, увеличиваются и тангенсы этих углов

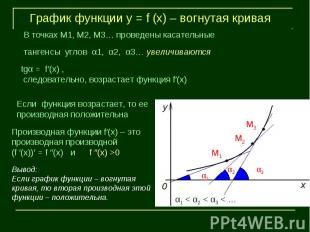
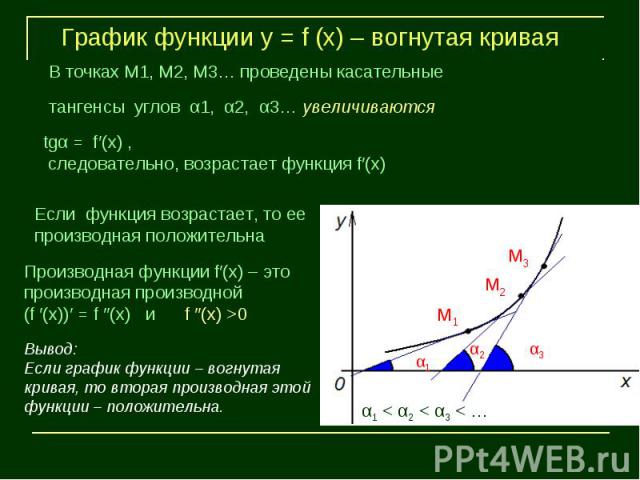
График функции у = f (х) – вогнутая криваяВ точках М1, М2, М3… проведены касательныетангенсы углов α1, α2, α3… увеличиваются следовательно, возрастает функция f′(х)Если функция возрастает, то ее производная положительнаПроизводная функции f′(х) – это производная производной Если график функции – вогнутая кривая, то вторая производная этой функции – положительна.

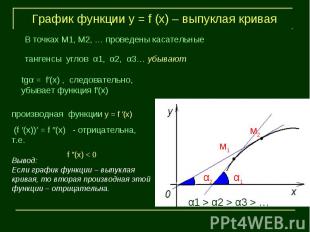
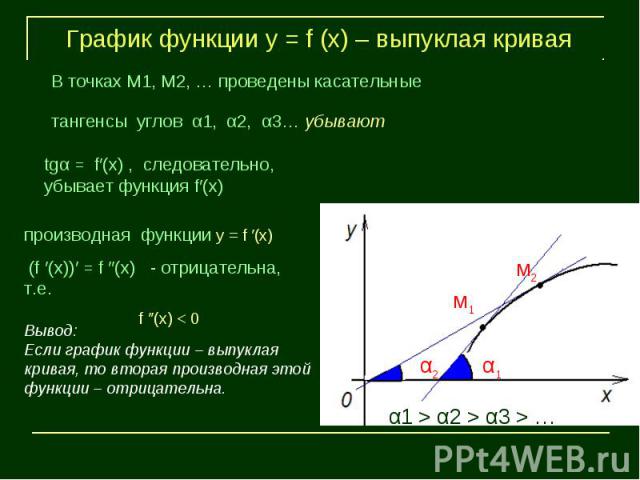
График функции у = f (х) – выпуклая криваяВывод:Если график функции – выпуклая кривая, то вторая производная этой функции – отрицательна.

Если вторая производная функции у = f (х) на данном интервале положительна, то кривая вогнута а если отрицательна – выпукла в этом промежутке

Точки, в которых выпуклость тость или наоборот, называются точками перегиба

Правило нахождения интервалов выпуклости и вогнутости графика функции:Найти:Вторую производнуюТочки, в которых она равна нулю или не существуетИнтервалы, на которые область определения разбивается этими точками Знаки второй производной в каждом интервалеЕсли f '‘(х) < 0, то кривая выпукла, если f '‘(х) > 0 – вогнута.

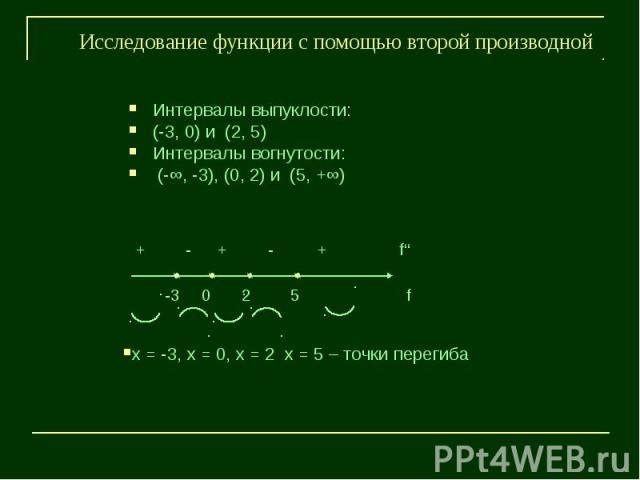
Исследование функции с помощью второй производнойИнтервалы выпуклости:(-3, 0) и (2, 5)Интервалы вогнутости: (-∞, -3), (0, 2) и (5, +∞)

График функции у = f (х) – вогнутая кривая График функции у = f (х) – выпуклая кривая

Найти интервалы выпуклости и вогнутости и точки перегиба

ПроверкаВариант 1у = х³ - 12х + 4х – любое числоf'(х) = 3х² - 12f''(х) = 6х6х = 0х = 0

ПроверкаВариант 2у = ¼ х4 – 3/2 х²х – любое числоf'(х) = х³ - 3хf''(х) = 3х² - 3 =3(х – 1)(х + 1)х = 1х = -1

Спасибо за работуУспехов!