Презентация на тему: Обратные тригонометрические функции

Эпиграф :Сегодня мы учимся вместе – Я, ваш учитель, и вы, мои ученики. Но в будущем ученик должен превзойти учителя, иначе в науке не будет прогресса В.А.Сухомлинский Обратные тригонометрические функции

I. Математический диктант

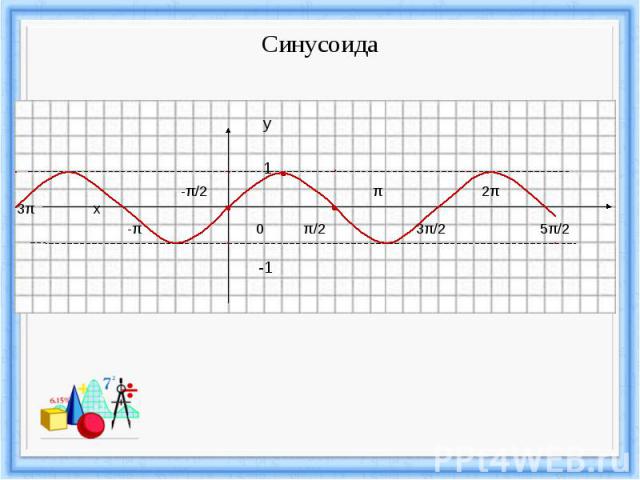
Функция y=sin x, график и свойства.

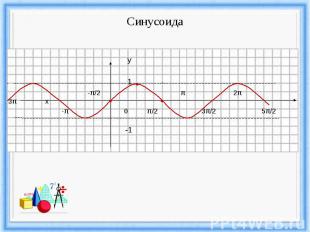
Синусоида

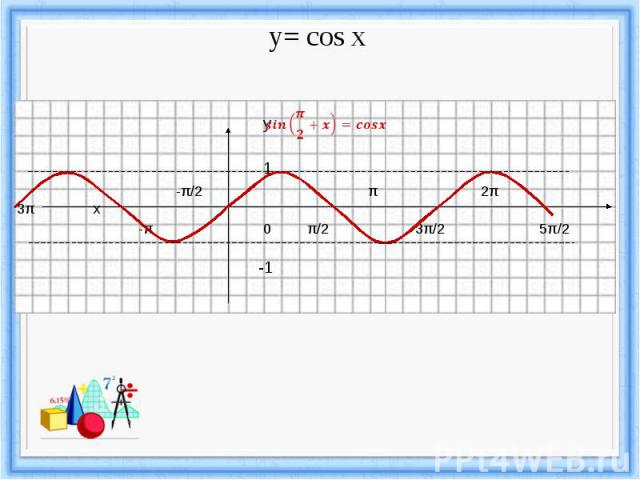
Функция y = cos x, её свойства и график.

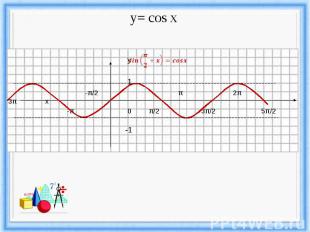
y= cos x

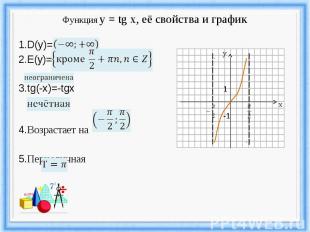
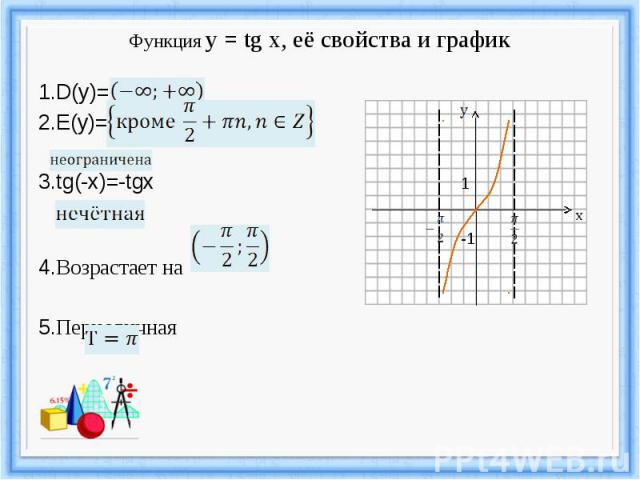
Функция y = tg x, её свойства и график

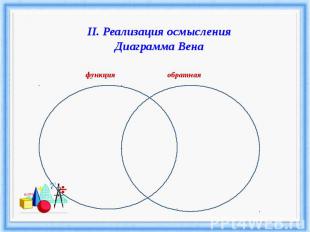
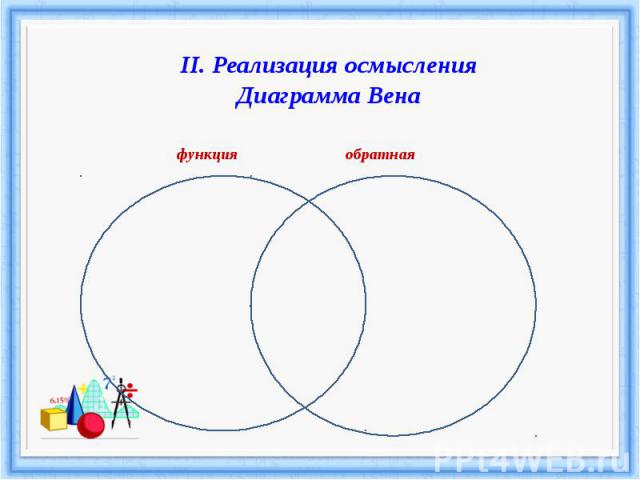
II. Реализация осмысленияДиаграмма Вена

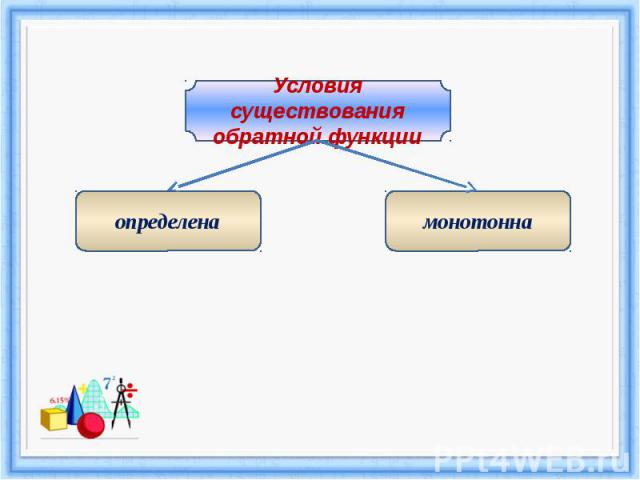
III. Проблемная ситуация1. Могут ли тригонометрические функции в своих областях определения иметь обратные себе функции?Ответ: да2. На всей области определения? И почему?Ответ: нет, так как не везде выполняется условие монотонности3.На каком промежутке монотонна функция синуса?Ответ: возрастает и принимает значение [-1;1].

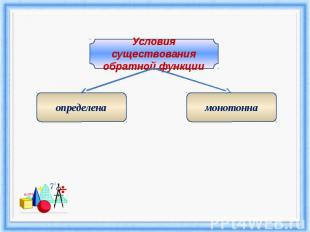
Условия существования обратной функцииопределенамонотонна

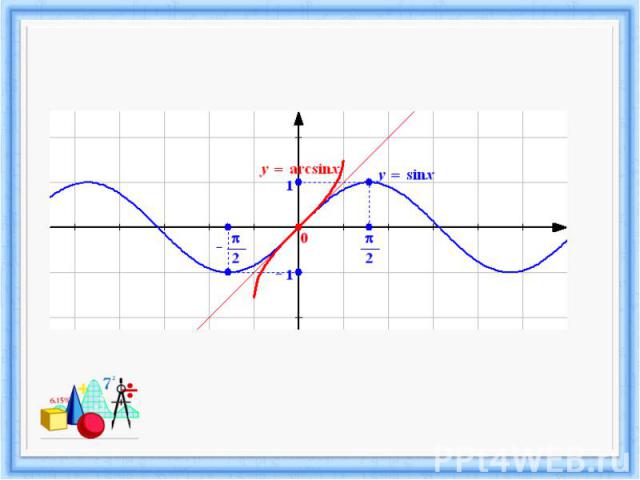
Графики симметричны относительно прямой у=х - ось симметрии

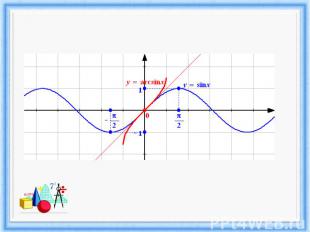
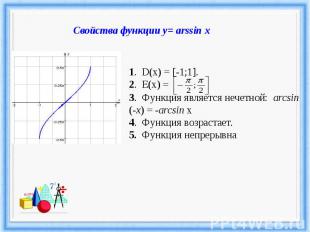
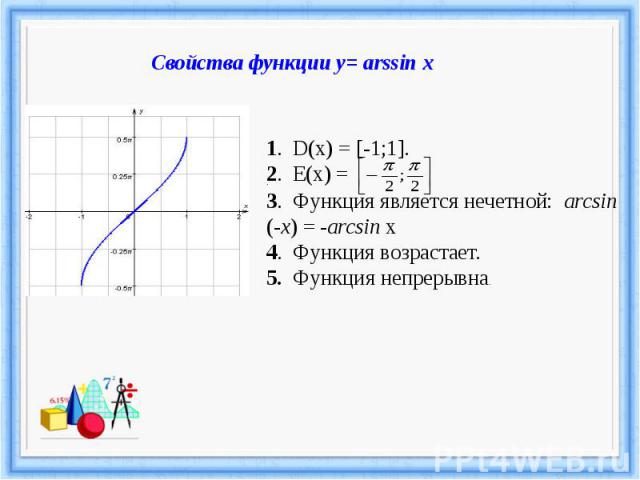
Свойства функции у= arssin x.3. Функция является нечетной: arcsin (-x) = -arcsin x 4. Функция возрастает.5. Функция непрерывна.

IV. Работа в группах Задание: работая по схеме, вместе нами разработанной , дайте определение, перечислите свойства и постройте график обратной функции для:

V. Инсерт

VI. РефлексияСинквейн (пятистишие)Одно существительноеДва прилагательныхТри глаголаФраза на тему синквейнаСуществительное синоним

VII. Подведение итоговVIII. Задание на дом: п.8 выучить определения и свойства, записать в тетради примеры из данного параграфа

Спасибо за урок!!!