Презентация на тему: Методы решения квадратного уравнения

Урок одной задачи. Методы решения квадратного уравнения.

Цель урока:Обобщить и систематизировать изученный материал по теме: «Квадратные уравнения».Рассмотреть несколько способов решения одной задачи и научиться выбирать из них наиболее оригинальный , оптимальный.Познакомиться с новыми приёмам устного решения квадратных уравнений.

Человеку, изучающему алгебру, часто полезнее решить одну задачу тремя различными способами, чем решать три-четыре различные задачи.Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт. У.У. Сойер

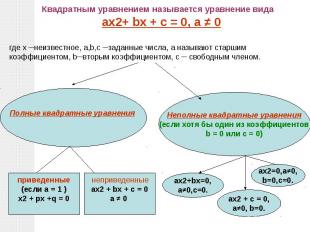
Квадратным уравнением называется уравнение вида ax2+ bx + c = 0, а ≠ 0где х ─неизвестное, a,b,c ─заданные числа, а называют старшим коэффициентом, b─вторым коэффициентом, c ─ свободным членом.

1) 2х² – х + 3 = 0 2) х² - 9х = 03) 4х + х² - 1 = 0 4) 2х – 5 = 05) 0,3 - 0,2х - х² = 0 6) 5х² = 07) -7х + х - 0,5 = 0 8) 49х² = 0 Какое из этих уравнений не является квадратным?Назовите неполные квадратные уравнения.Назовите приведенные квадратные уравнения.Какие уравнения можно решить по формуле корней квадратного уравнения?Какие уравнения можно решить разложением на множители, выделением квадрата двучлена, извлечением квадратного корня?

Найдите в каждой группе уравнений «лишнее»: А: 1. 3х2−х = 0, Б: 1. х2 −7х +1=0, 2. х2 −25 = 0, 2. 7х2 − 4х +8 = 0, 3. 4х2 + х −3 = 0, 3. х2 + 4х −4 = 0, 4. 4х2 = 0. 4. х2 −5х −3 = 0.Не решая уравнение х2 −8х + 7 = 0. Найдите: а) сумму корней: б) произведение корней: в) корни данного уравнения:

Первый способ( по общей формуле):С 1591 г. мы пользуемся формулами при решении квадратных уравнений

Задание 1: Решите квадратные уравнения :

Второй способ( по т., обратной теореме Виета): Уравнение, вида х2+pх+q=0, называется приведённым. Его корни можно найти по теореме, обратной теореме Виета: х1+х2=-p, х1∙х2=q.Например, уравнение х2-3х+2=0 имеет корни х1=2, х2=1 так как х1+х2=3, х1∙х2=2.

Задание 2. Решите приведённые квадратные уравнения по теореме, обратной теореме Виета.

Третий способ( формула корней приведенного квадратного уравнения):Корни уравнения вида х2+pх+q=0 можно найти по формуле:Задание 3: Решите квадратные уравнения по данной формуле:

Четвёртый способ( способ « переброски»): Решить квадратное уравнение можно способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант - точный квадрат.Например: Решим уравнение 2х2-11х+15=0. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение: у2-11у+30=0. По теореме, обратной теореме Виета у1= 5,у2= 6. тогда х1=у1/2, х2=у2/2; т.е. х1=2,5 , х2=3.

Решаем, используя метод «переброски»

Задание 3: Решите уравнения, используя метод «переброски»:

Пятый способ: « Способ коэффициентов»Пусть дано квадратное уравнение ах2+вх+с=0, где а≠0. 1.Если а+в+с=0(т.е.сумма коэффициентов уравнения равна нулю), то х1=1,х2=с/а. Например: 345х2-137х-208=0 (345-137-208=0), значит, х1= 1,х2= - 208/345. 2.Если а-в+с=0 (или в=а+с), то х1=-1,х2= - с/а. Например, 313х2+326х+13=0 (326=313+13), значит х1=-1,х2=-13/313.

Задание 4: Решите квадратные уравнения методом «коэффициентов»:

Урок одной задачи.Решить данное уравнение:По общей формуле;По теореме, обратной теореме Виета;По формуле для нахождения корней приведенного квадратного уравнения;Способом « переброса»;Способом коэффициентов.

Выводы: данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики; овладение данными приёмами поможет вам экономить время и эффективно решать уравнения; потребность в быстром решении обусловлена применением тестовой системы выпускных экзаменов.