Презентация на тему: Понятие квадратного корня

Площадь квадрата равна 64 см2. Площадь квадрата равна 64 см2. Найдите сторону квадрата

Для данного действительного числа b найдите действительное число а, такое, что а2 = b. Для данного действительного числа b найдите действительное число а, такое, что а2 = b. Покажем, что эта задача имеет решение, только, если b – неотрицательное число.

Если а = 0, то b = а2 = 0·0 = 0; Если а = 0, то b = а2 = 0·0 = 0; Если а > 0, то, b = а2 > 0; Если а < 0, то, b = а2 > 0; Вывод: Квадрат любого действительного числа – число неотрицательное.

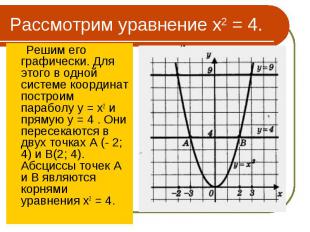
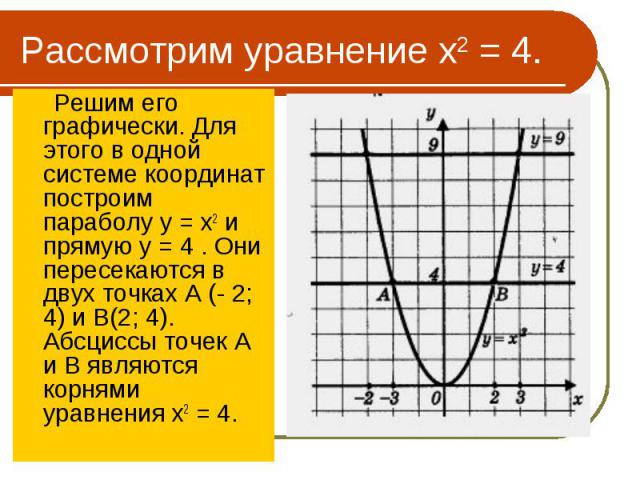
Решим его графически. Для этого в одной системе координат построим параболу у = х2 и прямую у = 4 . Они пересекаются в двух точках А (- 2; 4) и B(2; 4). Абсциссы точек А и В являются корнями уравнения х2 = 4. Решим его графически. Для этого в одной системе координат построим параболу у = х2 и прямую у = 4 . Они пересекаются в двух точках А (- 2; 4) и B(2; 4). Абсциссы точек А и В являются корнями уравнения х2 = 4.

Существует два числа, квадраты которых равны 4 Существует два числа, квадраты которых равны 4 22 = (-2)2 = 4 Аналогично: а2 = (-а)2 = b Если b = 0, то а =0

Квадратным корнем из данного числа называют такое число, квадрат которого равен данному числу Квадратным корнем из данного числа называют такое число, квадрат которого равен данному числу

Существует и притом только два квадратных корня из любого положительного числа b. Существует и притом только два квадратных корня из любого положительного числа b. Квадратный корень из нуля единственный, он равен нулю. Нет действительного числа – квадратного корня из отрицательного числа.

Числа 5 и -5 – квадратные корни из числа 25, потому что =(-5)2 =25 Числа 5 и -5 – квадратные корни из числа 25, потому что =(-5)2 =25

а)16 см2; б) 144 см2; в)169 см2; 625 км2; а)16 см2; б) 144 см2; в)169 см2; 625 км2; Какой таблицей при этом можно воспользоваться?

№ 114, № 115, № 116 № 114, № 115, № 116

Выучить определения п.3.1. Выучить определения п.3.1. №112, №117