Презентация на тему: Функции у = , их свойства и графики

Функции у = , их свойства и графики

Понятие корня n-й степени из действительного числаОпределение. Корнем n-й степени из неотрицательного числа а (n= 2,3,4,5…) называют такое неотрицательное число, при возведении в n-ю степень которого получается число а.Определение 2. Корнем нечетной степени n из отрицательного числа а (n= 3,5…) называют такое отрицательное число, при возведении в n-ю степень которого получается число а.

Работаем устно! Вычислить:Решить уравнение. Х4 = 16 У4 - 17 =0 Верно ли равенство:Расположите числа в порядке возрастания: 2, ,

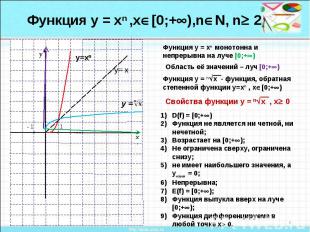
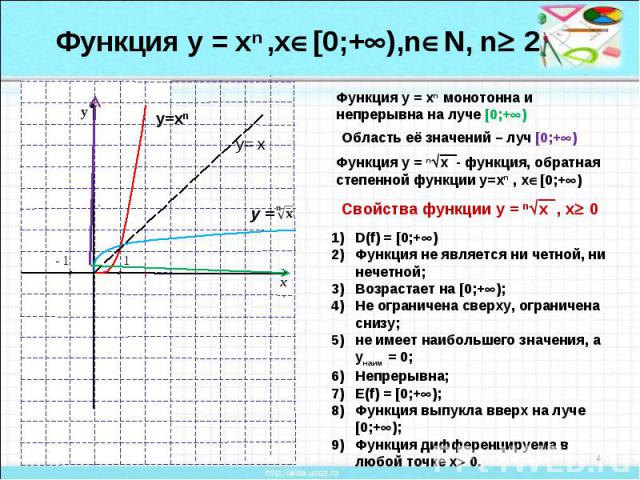
Функция у = хn ,х[0;+),nN, n 2Функция у = хn монотонна и непрерывна на луче [0;+) Функция у = nx - функция, обратная степенной функции у=хn , х[0;+)Свойства функции у = nx , х 0 D(f) = [0;+)Функция не является ни четной, ни нечетной;Возрастает на [0;+);Не ограничена сверху, ограничена снизу; не имеет наибольшего значения, а унаим = 0;Непрерывна;Е(f) = [0;+);Функция выпукла вверх на луче [0;+);Функция дифференцируема в любой точке х 0.

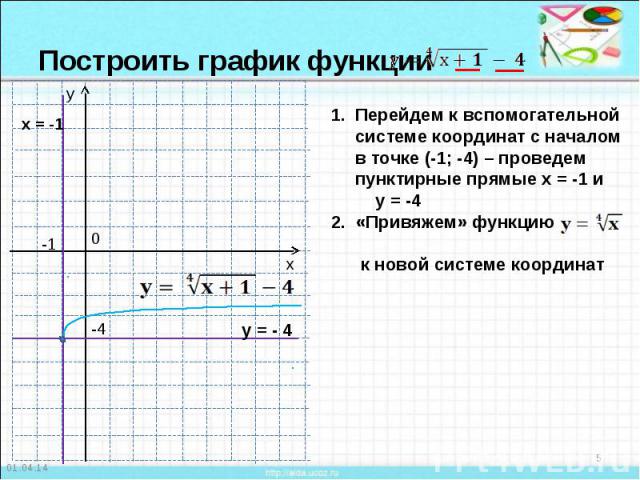
Построить график функции Перейдем к вспомогательной системе координат с началом в точке (-1; -4) – проведем пунктирные прямые х = -1 и у = -42. «Привяжем» функцию к новой системе координат

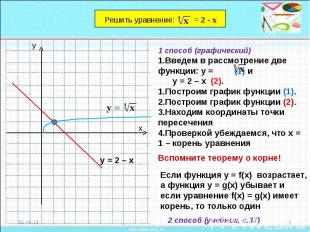
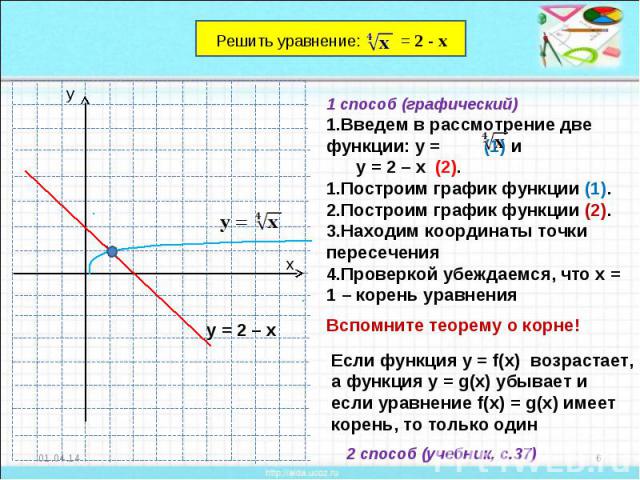
1 способ (графический)Введем в рассмотрение две функции: у = (1) и у = 2 – х (2).Построим график функции (1).Построим график функции (2).Находим координаты точки пересеченияПроверкой убеждаемся, что х = 1 – корень уравненияЕсли функция у = f(x) возрастает, а функция у = g(x) убывает и если уравнение f(x) = g(x) имеет корень, то только один

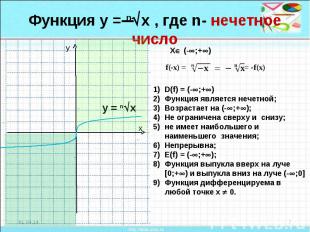
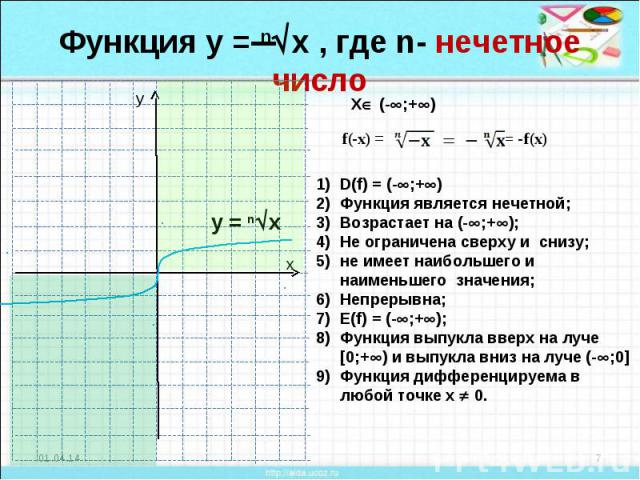
Функция у = nx , где n- нечетное числоD(f) = (-;+)Функция является нечетной;Возрастает на (-;+);Не ограничена сверху и снизу; не имеет наибольшего и наименьшего значения;Непрерывна;Е(f) = (-;+);Функция выпукла вверх на луче [0;+) и выпукла вниз на луче (-;0]Функция дифференцируема в любой точке х 0.