Презентация на тему: Разработка урока по алгебре и началам анализа в 10 физико-математическом классе.

Разработка урока по алгебре и началам анализа в 10 физико-математическом классе.МОУ многопрофильный лицей № 20 г. Ульяновска 2010-2011 уч. год

Работа учителя математики Ходзицкой Елены Александровны

Эта удивительнаяпроизводная!

Цель урока:Повторение, обобщение и систематизация изученного материала.Контроль знаний и умений.Подготовка к контрольной работе.

План урока:1.Организационный момент2.Вступление.Инструктаж.3.Проверка домашнего задания. 4.Повторение теоретического материала. Историческая справка. 4. Устная работа.Тест №1.5. Самостоятельная работа - тест№2.6. Решение задач. 7. Изучение нового материала. Теорема. 8. Самостоятельная работа - тест №3.9. Подведение итогов.

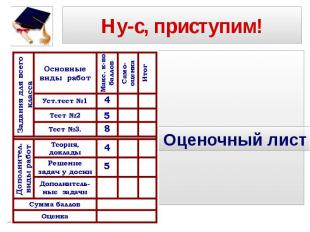
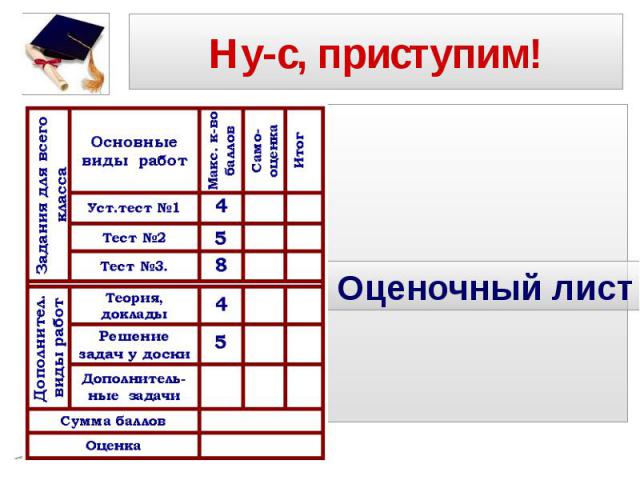
Оценочный лист

Ферма далеко продвинулся в применении дифференциальных методов, он использовал их не только для проведения касательных, но, к примеру, для нахождения максимумов, вычисления площадей. Однако ни Ферма, ни Декарт не сумели свести полученные научные выводы и результаты в единую систему. В 1638 году Ферма поделился этим открытием со своим земляком Рене Декартом, который также занимался этой проблемой и нашел свой метод построения касательных к алгебраическим кривым. Как родилась производная

Как родилась производная Многие из них легли в основу нового метода математического анализа – дифференциального исчисления, основоположниками которого считаются Вильям Лейбниц и Исаак Ньютон.

Как родилась производная Очень многие великие ученые внесли свой вклад в зарождение и развитие дифференциального исчисления

Внимание!Пришло время поработать!

Задание 1.Заполните таблицу №1:

Задание 1.Заполни таблицу №2: Задания такого рода будут выполняться в 11 классево время изучения темы «Интеграл».

Задание 2.Тест «Задачи в картинках» Правила работы: Прочитать условие задания;Продумать ответ(ы);По команде учителя поднять 1 или несколько карточек с номерами выбранных ответов.«Цена» 1 вопроса – 0,5 б. Удачи!

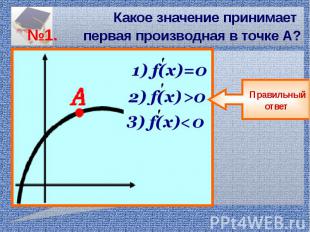
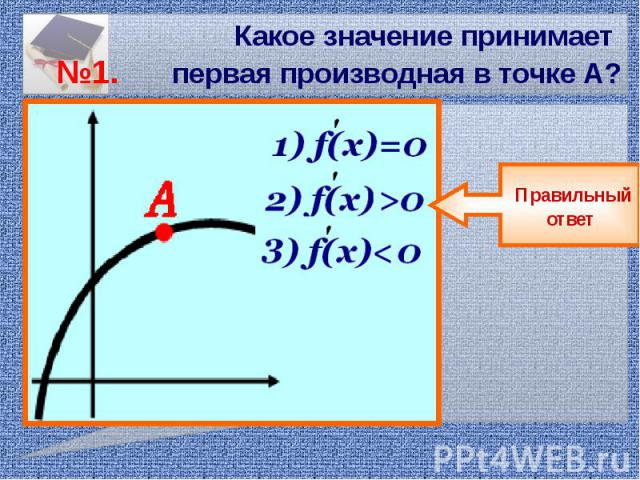
Какое значение принимает №1. первая производная в точке А?

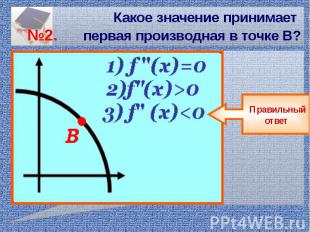
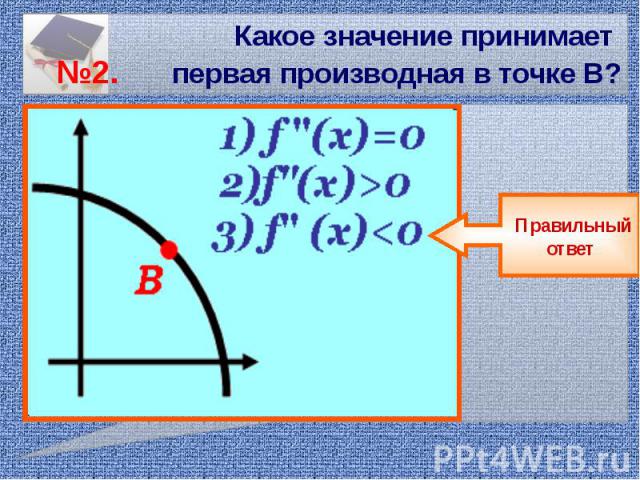
Какое значение принимает №2. первая производная в точке В?

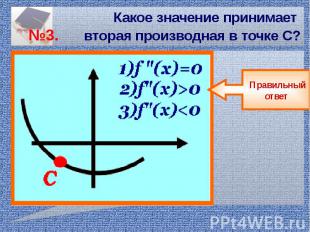
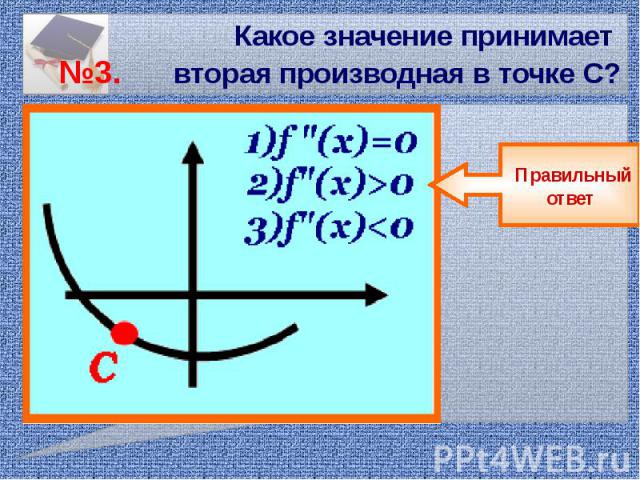
Какое значение принимает №3. вторая производная в точке С?

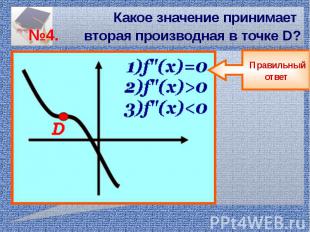
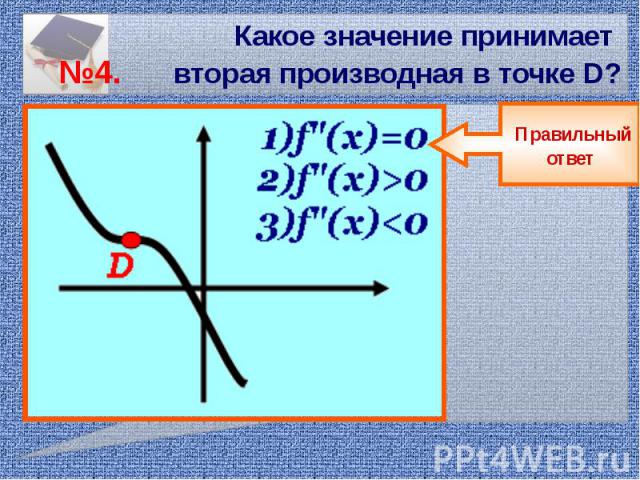
Какое значение принимает №4. вторая производная в точке D?

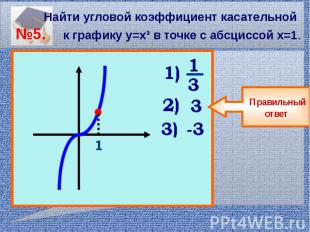
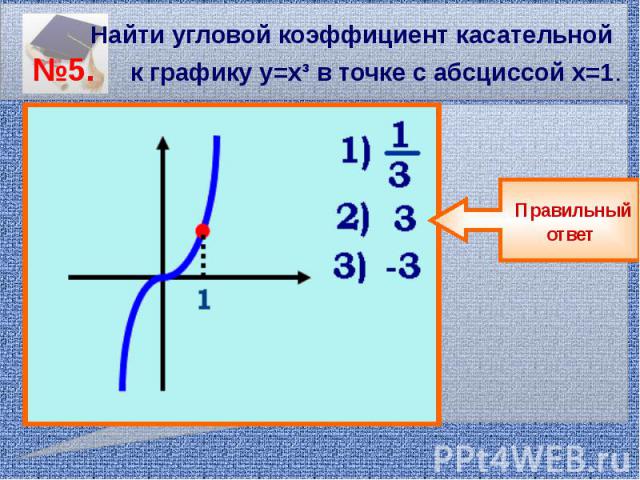
Найти угловой коэффициент касательной №5. к графику у=х³ в точке с абсциссой х=1.

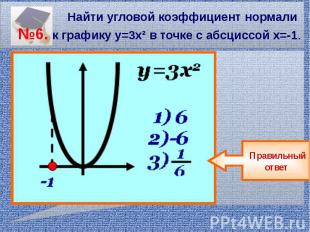
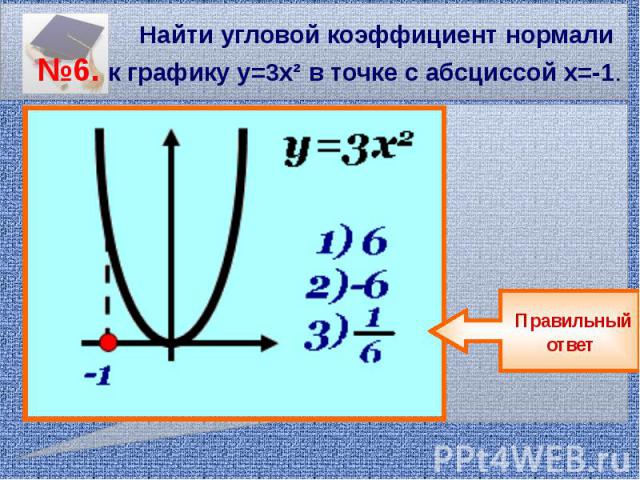
Найти угловой коэффициент нормали №6. к графику у=3х² в точке с абсциссой х=-1.

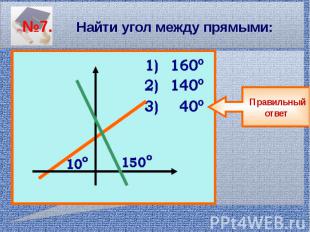
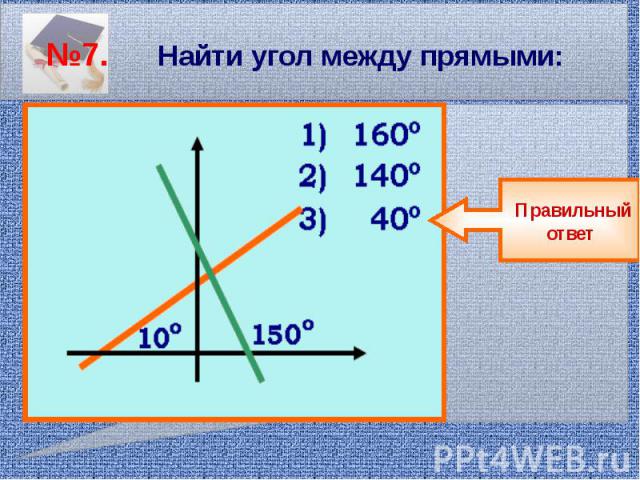
№7. Найти угол между прямыми:

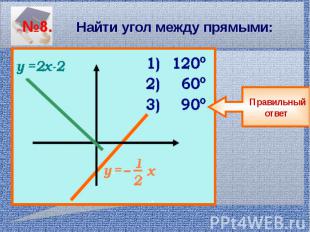
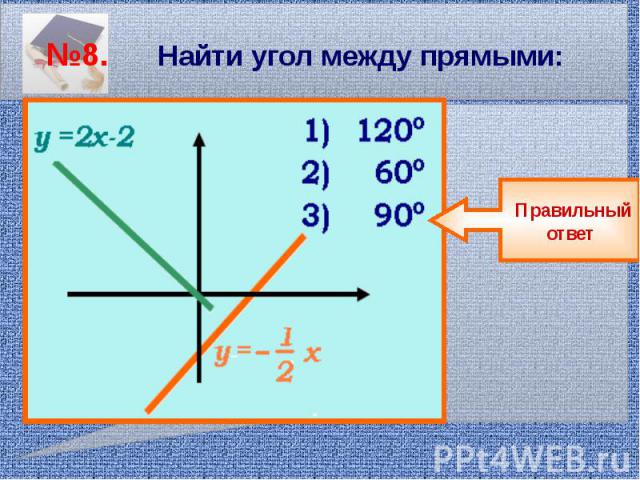
№8. Найти угол между прямыми:

Какие виды асимптот имеет №9. график функции? вертикальныегоризонтальныенаклонные

Какие виды асимптот имеет №10. график функции? вертикальные горизонтальные наклонные

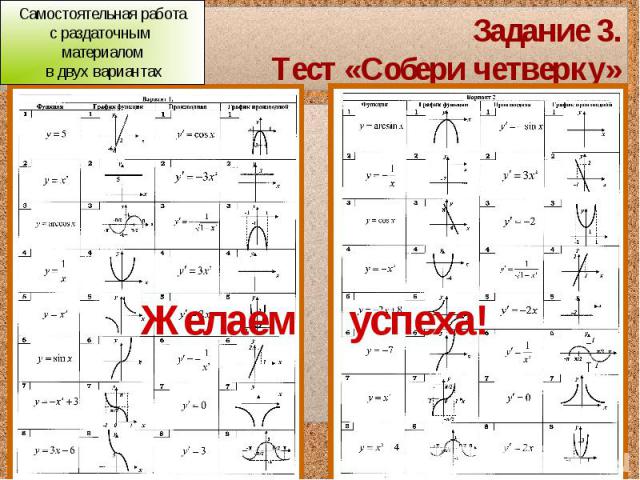
Задание 3.Тест «Собери четверку»

Задание 3.Тест «Собери четверку»

Самопроверка.Правильные ответы:1 вариант1-2-7-42-4-5-63-7-3-34-5-6-75-6-4-56-3-1-87-8-2-18-1-8-2

Внимание! Задачки потруднее!

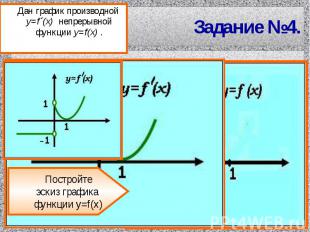
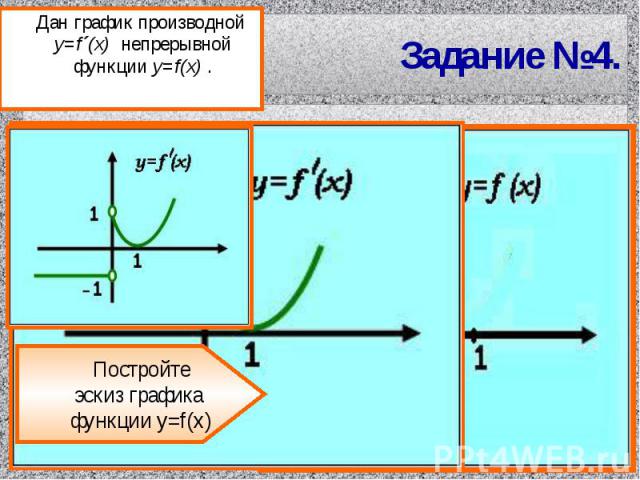
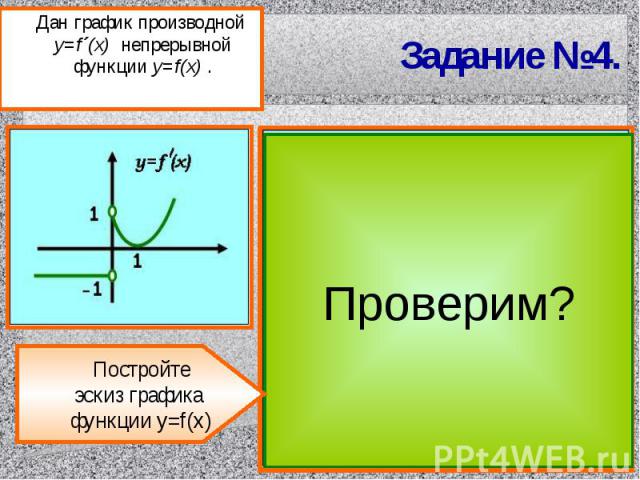
Задание №4. Дан график производной y=f´(x) непрерывной функции y=f(x) .Постройтеэскиз графика функции y=f(x)

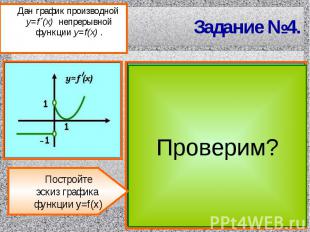
Задание №4. Дан график производной y=f´(x) непрерывной функции y=f(x) .Постройтеэскиз графика функции y=f(x)

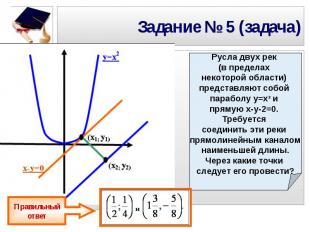
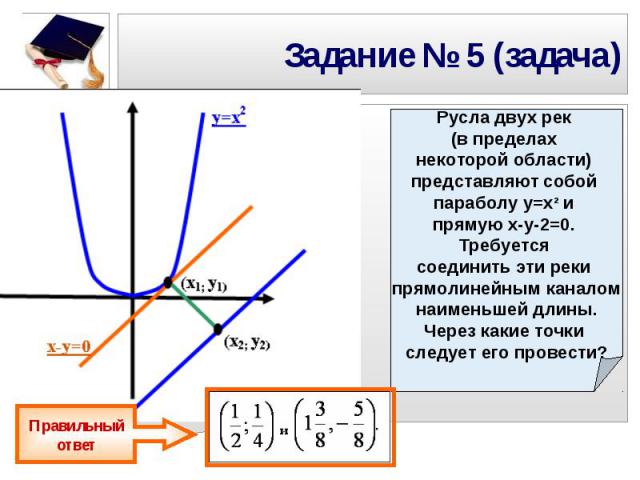
Задание № 5 (задача) Русла двух рек (в пределах некоторой области) представляют собой параболу у=х² и прямую х-у-2=0. Требуется соединить эти реки прямолинейным каналом наименьшей длины. Через какие точки следует его провести?

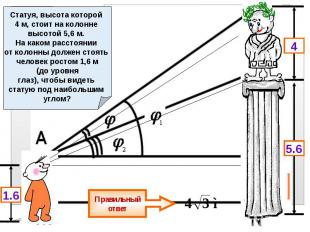
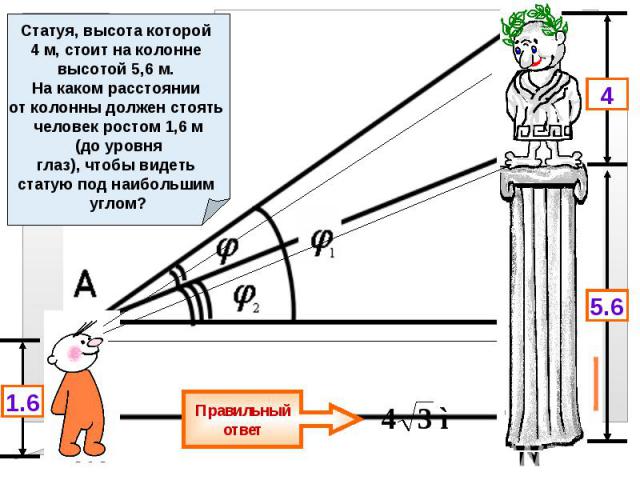
Задание № 6 (задача) Статуя, высота которой 4 м, стоит на колонне высотой 5,6 м. На каком расстоянии от колонны должен стоять человек ростом 1,6 м (до уровня глаз), чтобы видеть статую под наибольшим углом?

А сейчас кое-что новенькое!

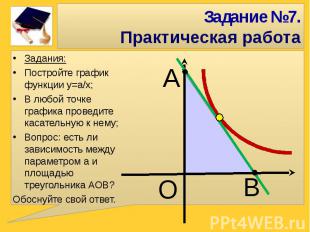
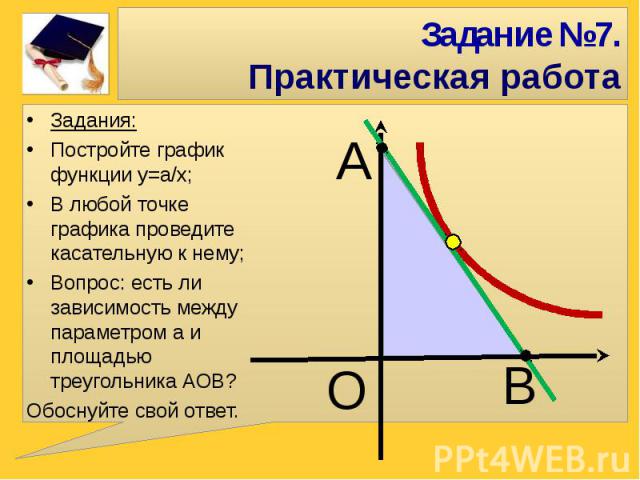
Задания:Постройте график функции у=а/х;В любой точке графика проведите касательную к нему;Вопрос: есть ли зависимость между параметром а и площадью треугольника АОВ?Обоснуйте свой ответ.

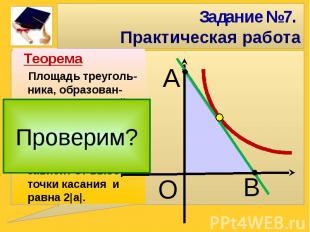
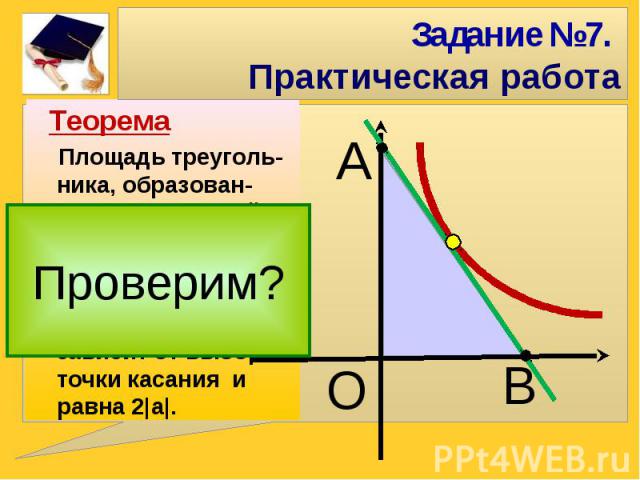
Задание №7. Практическая работаПлощадь треуголь-ника, образован-ного касательной, проведенной к графику функции у=а/х, и осями координат, не зависит от выбора точки касания и равна 2|а|.

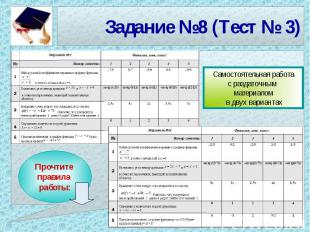
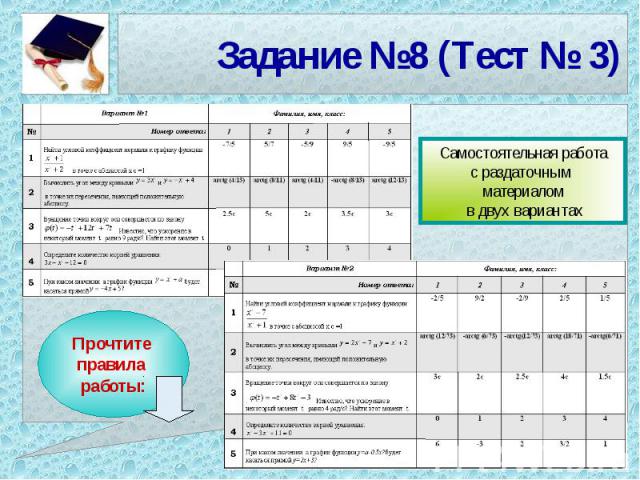
Задание №8 (Тест № 3)

Задание №8 (Тест № 3)Желаем успеха! Правила работы: Решить задачу;Найти полученный ответ в тесте;В соответствующем окошке поставить метку: или

Задание №8 (Тест № 3) Вариант №1-9/5arctg (8/11)2,5 c1 кореньа=9Вариант №2-2/9arctg (6/73)2 c1 кореньа=1

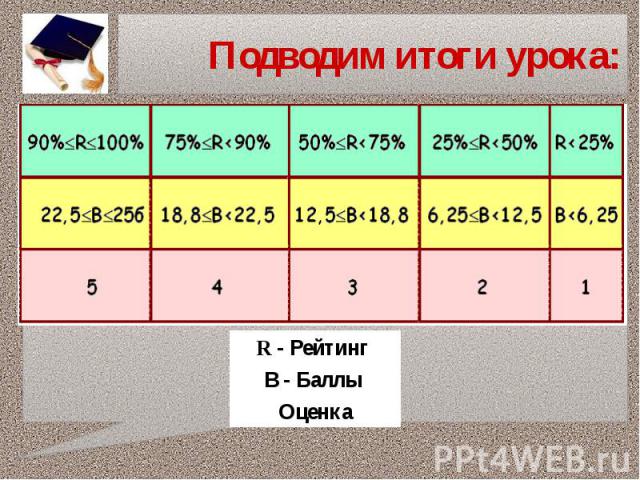
Подводим итоги урока:Назовите имена учёных, внёсших вклад в создание и развитие дифференциального исчисления.С какими новыми понятиями вы познакомились в процессе изучения темы?Какие новые алгоритмы стали вам известны? Задачи какого рода решаются с помощью производной?Назовите сферы приложения производной.

Подводим итоги урока:Вспомните, каковы были цели, поставленные нами в начале урока?Достигнуты ли цели?Что удалось?Что не получилось?Понравился ли вам урок?

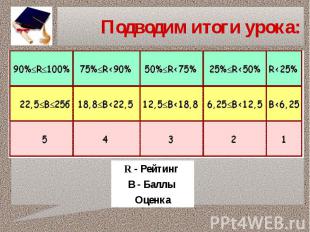
Подводим итоги урока:

Спасибо за урок!