Презентация на тему: Признаки параллелограмма

Признаки параллелограмма Цель урока: Рассмотреть признаки параллелограмма и закрепить полученные знания в процессе решения задач.

Дополнительные свойства параллелограмма 1°. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.2°. Биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы противоположных углов параллельны или лежат на одной прямой.

Индивидуальная работа по карточкам

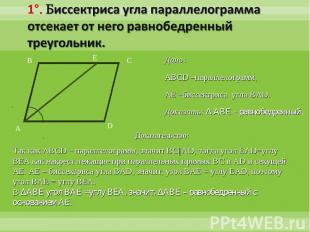
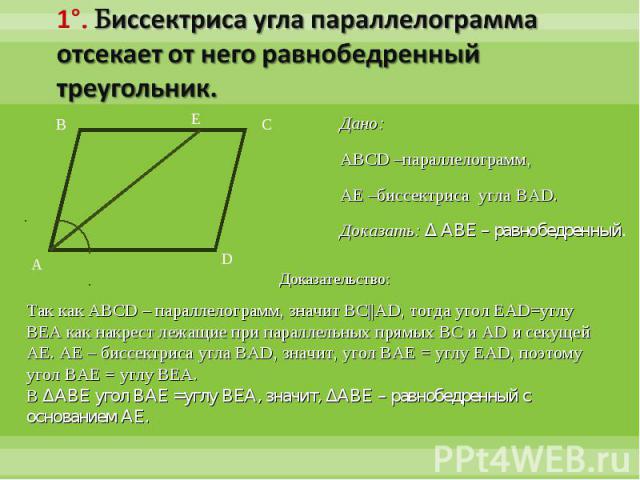
1°. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.Дано:ABCD –параллелограмм, AE –биссектриса угла BAD.Доказать: Δ ABE – равнобедренный.Доказательство:Так как ABCD – параллелограмм, значит BC||AD, тогда угол EAD=углу BEA как накрест лежащие при параллельных прямых BC и AD и секущей AE. AE – биссектриса угла BAD, значит, угол BAE = углу EAD, поэтому угол BAE = углу BEA.В ΔABE угол BAE =углу BEA, значит, ΔABE – равнобедренный с основанием AE.

2°. Биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы противоположных углов параллельны или лежат на одной прямой.Дано:ABCD –параллелограмм, BE –биссектриса угла CBA,AE – биссектриса угла BAD.Доказательство:

СвойствоПризнакОбратная теорема

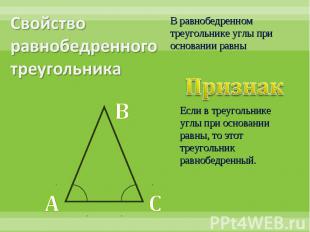
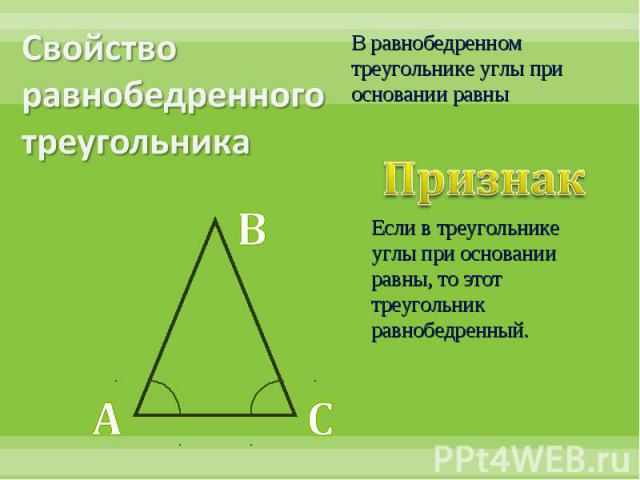
Свойство равнобедренного треугольникаВ равнобедренном треугольнике углы при основании равныПризнак Если в треугольнике углы при основании равны, то этот треугольник равнобедренный.

Признаки параллелограммаЕсли в четырехугольнике две стороны равны и параллельны, то это четырехугольник – параллелограмм.Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

1°. Если AB=CD и AB||CD, то ABCD-параллелограмм.Дано:ABCD –четырехугольник. AB=CD и AB||CD.Доказать, что ABCD-параллелограмм.Доказательство:

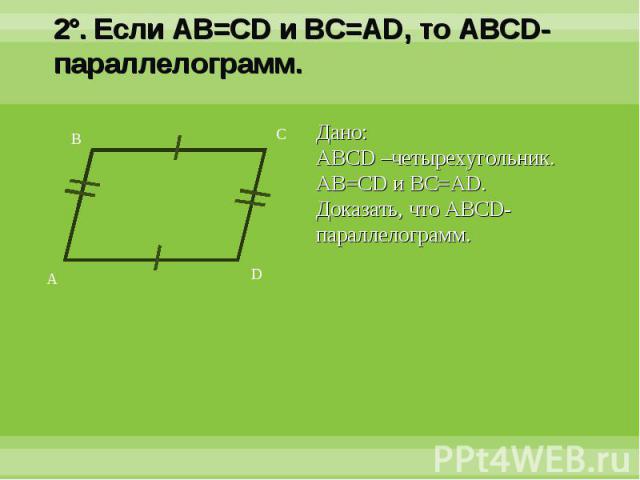
2°. Если AB=CD и BC=AD, то ABCD-параллелограмм.Дано:ABCD –четырехугольник. AB=CD и BC=AD.Доказать, что ABCD-параллелограмм.

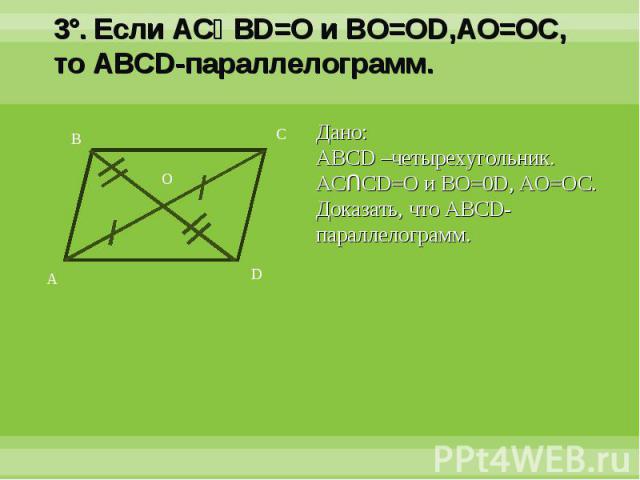
3°. Если ACՈBD=O и BO=OD,AO=OC, то ABCD-параллелограмм.Дано:ABCD –четырехугольник. ACՈCD=O и BO=0D, AO=OC.Доказать, что ABCD-параллелограмм.

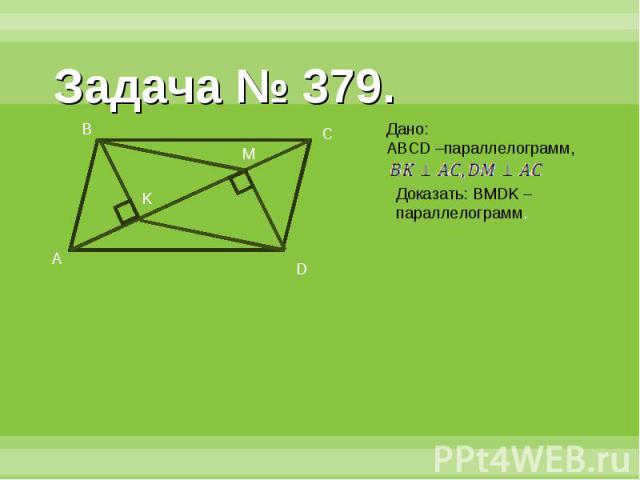
Задача № 379.Дано:ABCD –параллелограмм, Доказать: BMDK – параллелограмм.

Самостоятельное решение задач

Задача №1.Дано:ABCD- параллелограмм, M- середина BC, N – середина AD.Доказать: AMCN –параллелограмм.Доказательство:Так как M – середина BC, N – середина AD, то BM=MC, AN=ND. Но BC=AD как противолежащие стороны параллелограмма, тогда MC = AN. BC||AD как противолежащие стороны параллелограмма, значит MC||AN. В четырехугольнике AMCN противолежащие стороны MC и AN равны и параллельны, следовательно, AMNC – параллелограмм.

Задача №2.Дано:ΔABC - треугольник, АM- медиана, DєAM, AM=MD.Доказать: ABDC –параллелограмм.Доказательство:Так как AM – медиана Δ ABC, то CM=BM. По Построению AM=DM. Получили, что в четырехугольнике ABCD диагонали AD и BC пересекаются в точке M и точкой пересечения делятся пополам, следовательно, ABDC – параллелограмм.

Задача №3.Дано:ABCD- параллелограмм, K,L,M и N- середины сторон соответственно AB, BC, CD, AD.Доказать, что четырехугольник с вершинами в точках пересечения прямых AL, BM, CN, DK - параллелограмм.

Дано:ABCD- параллелограмм, K,L,M и N- середины сторон соответственно AB, BC, CD, AD.Доказать, что четырехугольник с вершинами в точках пересечения прямых AL, BM, CN, DK - параллелограмм.Доказательство:По условию задачи AM:MB=BN:NC=CK:KD=DL:AL. В параллелограмме ABCD AB=CD, BC=AD, тогда AM=CK, BM=KD, BN=DL, NC=LA. ΔNCK=ΔLAM, ΔMBN=ΔDKL по двум сторонам и углу между ними ( угол A=углу С, угол В=углу D как противолежащие углы параллелограмма), тогда MN=KL, NK=ML, следовательно, в четырехугольнике MNKL противолежащие стороны равны, а это значит, что MNKL – параллелограмм.

Домашнее задание П. 43, вопрос 9.Решить задачи №383, №373, №374( устно); решить задачу №12 из рабочей тетради.