Презентация на тему: Признаки параллелограмма


рассмотреть признаки параллелограмма и закрепить полученные знания в процессе решения задач; рассмотреть признаки параллелограмма и закрепить полученные знания в процессе решения задач; совершенствовать навыки решения задач.

Что такое параллелограмм? Что такое параллелограмм? Сформулируйте свойства: противоположных сторон; противоположных углов параллелограмма диагоналей параллелограмма односторонних углов параллелограмма
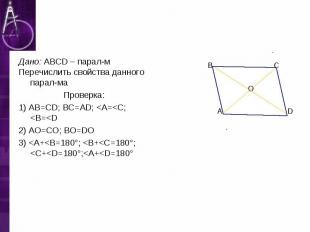
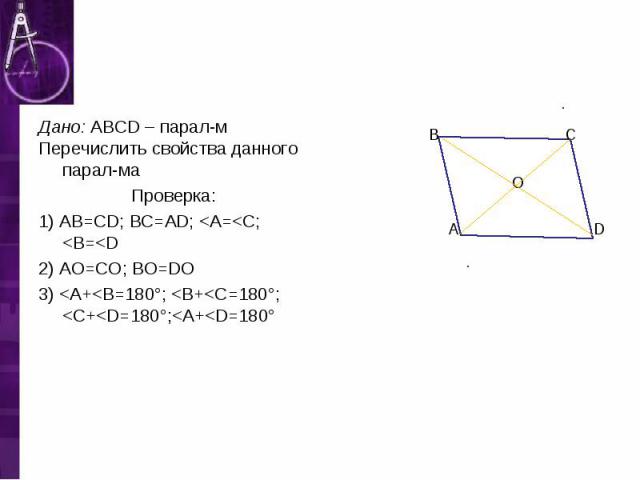
Дано: ABCD – парал-м Дано: ABCD – парал-м Перечислить свойства данного парал-ма Проверка: 1) АВ=CD; BC=AD; <A=<C; <B=<D 2) АО=СО; ВО=DO 3) <A+<B=180°; <B+<C=180°; <C+<D=180°;<A+<D=180°
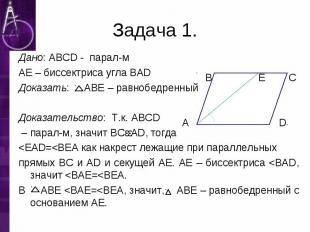
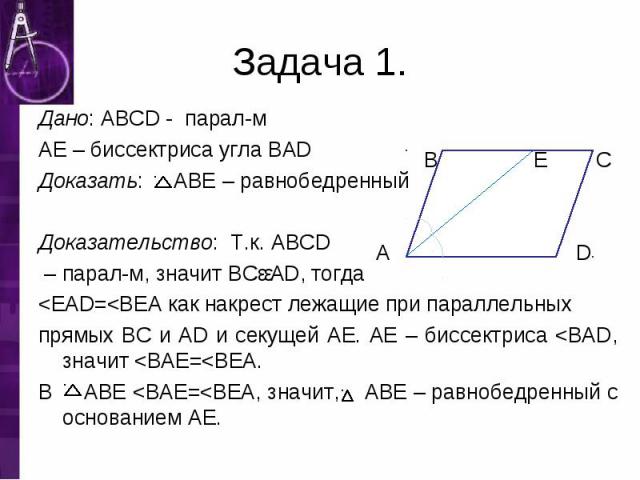
Дано: ABCD - парал-м Дано: ABCD - парал-м AE – биссектриса угла BAD Доказать: ABE – равнобедренный Доказательство: Т.к. ABCD – парал-м, значит BCǀǀAD, тогда <EAD=<BEA как накрест лежащие при параллельных прямых BC и AD и секущей AE. AE – биссектриса <BAD, значит <BAE=<BEA. В ABE <BAE=<BEA, значит, ABE – равнобедренный с основанием AE.

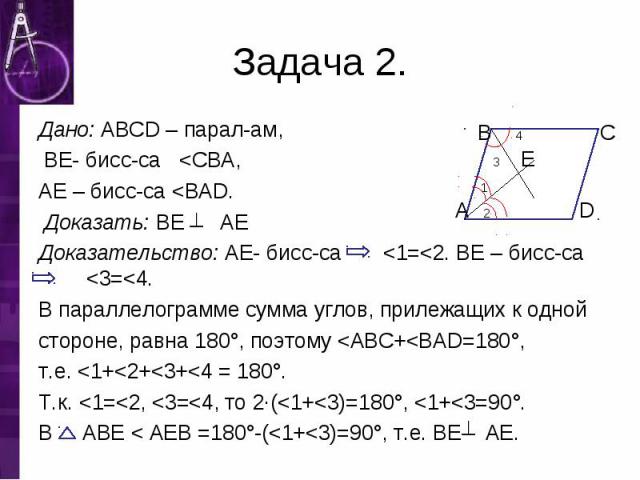
Дано: ABCD – парал-ам, Дано: ABCD – парал-ам, BE- бисс-са <CBA, AE – бисс-са <BAD. Доказать: BE AE Доказательство: AE- бисс-са <1=<2. BE – бисс-са <3=<4. В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°, поэтому <ABC+<BAD=180°, т.е. <1+<2+<3+<4 = 180°. Т.к. <1=<2, <3=<4, то 2·(<1+<3)=180°, <1+<3=90°. В ABE < AEB =180°-(<1+<3)=90°, т.е. ВЕ АЕ.

Что означают слова «свойства» и «признак»? Что такое обратная теорема? Всегда ли верно утверждение, обратное данному? Приведите примеры
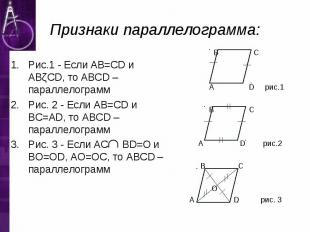
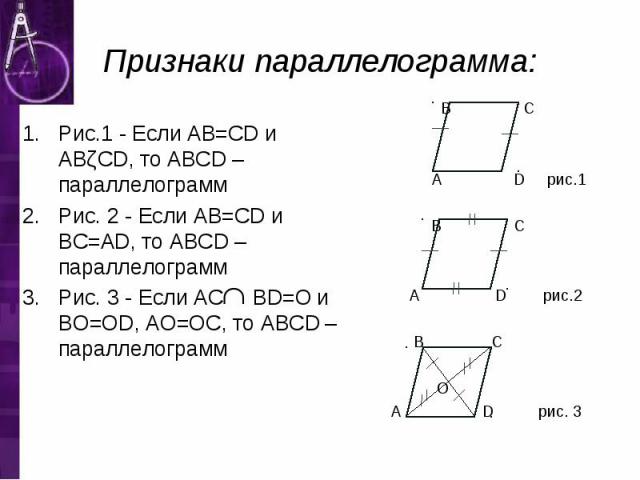
Рис.1 - Если AB=CD и ABǁCD, то ABCD – параллелограмм Рис. 2 - Если AB=CD и BC=AD, то ABCD – параллелограмм Рис. 3 - Если AC BD=O и BO=OD, AO=OC, то ABCD – параллелограмм
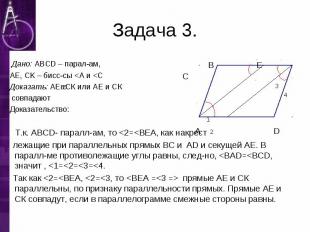
Дано: ABCD – парал-ам, Дано: ABCD – парал-ам, AE, CK – бисс-сы <A и <C Доказать: АЕǀǀСК или АЕ и СК совпадают Доказательство: Т.к. ABCD- паралл-ам, то <2=<BEA, как накрест лежащие при параллельных прямых BC и AD и секущей АЕ. В паралл-ме противолежащие углы равны, след-но, <BAD=<BCD, значит , <1=<2=<3=<4. Так как <2=<BEA, <2=<3, то <BEA =<3 => прямые АЕ и СК параллельны, по признаку параллельности прямых. Прямые АЕ и СК совпадут, если в параллелограмме смежные стороны равны.

Дано: ABCD – параллелограмм, Дано: ABCD – параллелограмм, ВК АС, DM АС Доказать: BMDK – параллелограмм Доказательство: BKC= DMA по гипотенузе и острому углу (<BCK=<DAC как накрест лежащие углы при параллельных прямых AD и BC и секущей АC, BC=AD как противолежащие стороны паралл-ма, ВKC= DMA прямоугольные), значит MD=BK. ВМК= DKM – прямоугольные, BMK = DKM по двум катетам (MD=BK, KM- общий катет), значит BM=DK. В четырехугольнике BMDK противолежащие стороны равны (MD=BK и BM=DK), следовательно BMDK – параллелограмм.

Вариант 1. Вариант 1. Дано: ABCD – паралл-ам М – середина ВС, N – середина AD Доказать: AMCN – параллелограмм В M С А N D 2. В треугольнике ABC медиана АМ продолжена за точку М до точки D на расстояние, равное AM, так, что AM=MD. Докажите, что ABDC - параллелограмм

п. 43, вопрос 9 п. 43, вопрос 9 Задачи № 383, 373, 378

Учебник «Геометрия 7-9», автор Учебник «Геометрия 7-9», автор Л.С. Атанасян и др. 2. «Поурочные разработки по геометрии. 7 класс» Н.Ф.Гаврилова