Презентация на тему: Правильные многогранники

Данная программа предназначена для частного просмотра. Данная программа предназначена для частного просмотра. За несанкционированное изготовление копий, коммерческий прокат, трансляцию по кабельным и эфирным каналам телевидения установлена ответственность, предусмотренная ст. 48, 49 Закона РФ “Об авторских и смежных правах” ст. 150 п. 4 кодекса об административных правонарушениях и ст. 146 Уголовного кодекса Российской Федерации.

Специально для тех кто не любит геометрию Специально для тех кто не любит геометрию Представляет Художественный фильм “Правильные многогранники”

1) Симметрия в пространстве. 1) Симметрия в пространстве. 2) Понятие правильного многогранника. 3) Элементы симметрии правильных многогранников. Скандалы, интриги, расследования.

Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О- середина отрезка АА1 (рис. 1). Точка О считается симметричной самой себе. Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О- середина отрезка АА1 (рис. 1). Точка О считается симметричной самой себе.

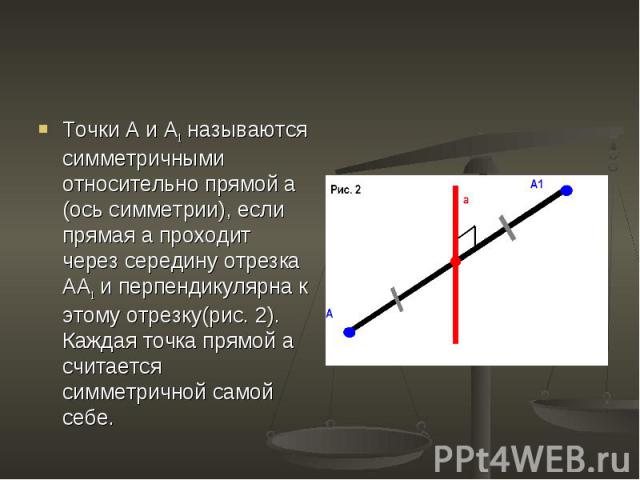
Точки А и А1 называются симметричными относительно прямой а (ось симметрии), если прямая а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку(рис. 2). Каждая точка прямой а считается симметричной самой себе. Точки А и А1 называются симметричными относительно прямой а (ось симметрии), если прямая а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку(рис. 2). Каждая точка прямой а считается симметричной самой себе.  

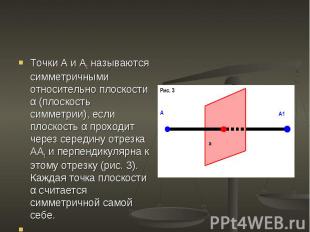
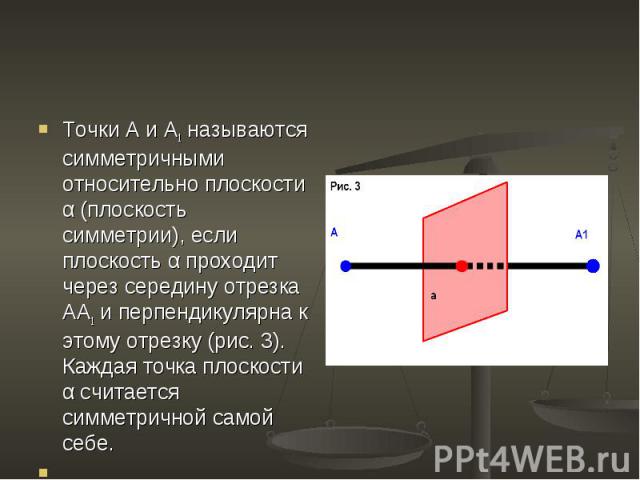
Точки А и А1 называются симметричными относительно плоскости α (плоскость симметрии), если плоскость α проходит через середину отрезка АА1 и перпендикулярна к этому отрезку (рис. 3). Каждая точка плоскости α считается симметричной самой себе. Точки А и А1 называются симметричными относительно плоскости α (плоскость симметрии), если плоскость α проходит через середину отрезка АА1 и перпендикулярна к этому отрезку (рис. 3). Каждая точка плоскости α считается симметричной самой себе.  

Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрию фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Фигура может иметь один или несколько центров симметрии. С симметрией мы часто встречаемся в природе, архитектуре, технике, быту. Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрию фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Фигура может иметь один или несколько центров симметрии. С симметрией мы часто встречаемся в природе, архитектуре, технике, быту.

Многие здания симметричны относительно плоскости, например главное здание Московского государственного университета. Почти все кристаллы, встречающиеся в природе, имеют центр, ось или плоскость симметрии. В геометрии центр, ось и плоскость симметрии многогранника называются элементами симметрии этого многогранника.

Выпуклый многогранник называется правильным, если все его грани- равные правильные многоугольники и в каждой его вершине сходиться одно и то же число ребер. Примером правильного многогранника является куб. Все его грани- равные квадраты, и в каждой вершине сходятся три ребра. Всего существует 5 правильных многогранников, других видов правильных многогранников нет. Выпуклый многогранник называется правильным, если все его грани- равные правильные многоугольники и в каждой его вершине сходиться одно и то же число ребер. Примером правильного многогранника является куб. Все его грани- равные квадраты, и в каждой вершине сходятся три ребра. Всего существует 5 правильных многогранников, других видов правильных многогранников нет.

Составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно сумма плоских углов при каждой вершине равна 180°. Составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно сумма плоских углов при каждой вершине равна 180°.

Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно сумма плоских углов при каждой вершине равна 240°. Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно сумма плоских углов при каждой вершине равна 240°.

Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно сумма плоских углов при каждой вершине равна 300 °. Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно сумма плоских углов при каждой вершине равна 300 °.

Составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270 °. Составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270 °.

Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°. Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.

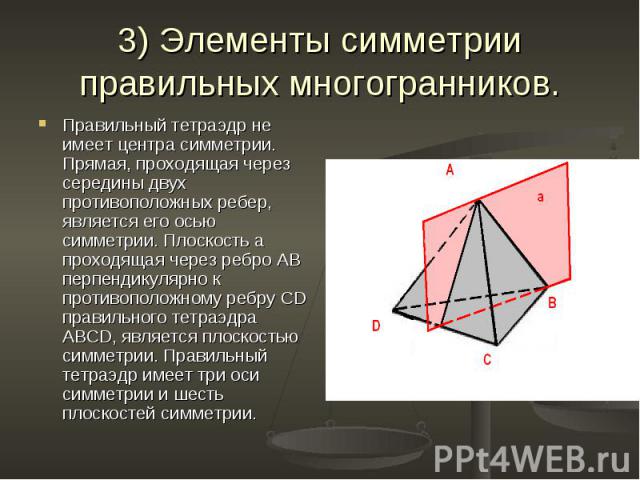
Правильный тетраэдр не имеет центра симметрии. Прямая, проходящая через середины двух противоположных ребер, является его осью симметрии. Плоскость а проходящая через ребро АВ перпендикулярно к противоположному ребру СD правильного тетраэдра ABCD, является плоскостью симметрии. Правильный тетраэдр имеет три оси симметрии и шесть плоскостей симметрии. Правильный тетраэдр не имеет центра симметрии. Прямая, проходящая через середины двух противоположных ребер, является его осью симметрии. Плоскость а проходящая через ребро АВ перпендикулярно к противоположному ребру СD правильного тетраэдра ABCD, является плоскостью симметрии. Правильный тетраэдр имеет три оси симметрии и шесть плоскостей симметрии.

Куб имеет один центр симметрии- точку пересечения его диагоналей. Куб имеет девять осей симметрии и девять плоскостей симметрии. Правильный октаэдр, правильный икосаэдр, правильный додекаэдр имеют центр симметрии и несколько осей и плоскостей симметрии. Куб имеет один центр симметрии- точку пересечения его диагоналей. Куб имеет девять осей симметрии и девять плоскостей симметрии. Правильный октаэдр, правильный икосаэдр, правильный додекаэдр имеют центр симметрии и несколько осей и плоскостей симметрии.

Матвеев Андрей = E100nec = Матвеев Андрей = E100nec = Ефремов Игорь = 1grek = Гордеев Денис = Gorden = Медведев Гриша = gR1ZzLy = Аксаков Вова = F@r$ = |Научный консультант: учитель математики Маркова З.Г. МОУ СОШ №6 г.Чебоксары - 2008