Презентация на тему: Особенности математических способностей одаренных детей и их развитие в условиях внеклассной работы

ОСОБЕННОСТИ МАТЕМАТИЧЕСКИХ СПОСОБНОСТЕЙ ОДАРЕННЫХ ДЕТЕЙ И ИХ РАЗВИТИЕ В УСЛОВИЯХ ВНЕКЛАССНОЙ РАБОТЫ

Ученик - это не сосуд, который надо наполнить, а факел, который надо зажечь.Плутарх

Под одаренностью ребенка понимаются более высокая, чем у его сверстников при прочих равных условиях, восприимчивость к учению и более выраженные творческие проявления.

 Выделяют три категории одаренных в умственном отношении детей: дети с необыкновенно высоким общим уровнем умственного развития при прочих равных условиях;дети с признаками специальной умственной одаренности (профильная одаренность);дети потенциально одаренные, обладающие яркой познавательной активностью и незаурядными умственными резервами, но не достигшие успехов в учении и пока себя не проявившие.

способность извлекать необходимую информацию из заданной конфигурации путем ее анализа или дополнения, включая поиск идеи решения задачи с помощью рисунков, моделей фигур или мысленного представления;способность к переводу на язык геометрии той или иной задачи и обращение к наглядным образам в процессе решения негеометрических задач.способность применять известные алгоритмы и методы в конкретной ситуации;способность свести задачу к выполнению конечной цепи более элементарных действий;способность довести до конца намеченный план решения, применяя аналитические методы, относящиеся к алгебре, тригонометрии, векторной алгебре или анализу.в вычленении (из некоторого общего положения) и исследовании всех частных случаев, в создании экономной и непротиворечивой схемы решения задачи, в проведении доказательных рассуждений, использующих, в частности, прием доказательства «от противного», обращение к контрпримеру, продвижение при решении задач «от конца к началу» и другие приемы.

Критерии выявления математических способностей учащихся в ходе решения задач СкоростьПрочностьГлубина

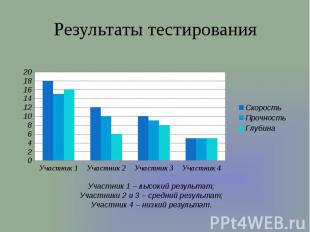
Результаты тестирования Участник 1 – высокий результат;Участники 2 и 3 – средний результат;Участник 4 – низкий результат.

Система работы по развитию математических способностей учащихся во внеурочной деятельности 1 этап разработка программы 2 этап тестирование учащихся и формирование группы3 этап работа по реализации программы в группе

Цель кружковой работы увлечь учащихся математикой, помочь почувствовать ее красоту, пробудить интерес к математике у тех, кто его до сих пор не испытывал, дать возможность учащимся обнаружить в себе математические способности;развивать творческие способности у учащихся, умение самостоятельно добывать знания;расширить и углубить базовую программу по математике;реализовать личностно-ориентированный подход в обучении математике.

Задачи кружковой работы: Привитие интереса к математическим знаниям;Развитие математического кругозора;Привитие навыков самостоятельной работы;Развитие математического мышления, смекалки, эрудиции;Показать связь математики с жизнью.

Стратегии УскорениеИндивидуализацияОбогащение

Основные формы проведения кружковой работы: решение задач занимательного характера, задач на смекалку, разбор математических софизмов, проведение математических игр; математический бой, турниры, эстафеты, викторины;устные или письменные олимпиады;заслушивание рефератов учащихся;научно-исследовательская работа.

«Математические бои»

Участники олимпиады «Авангард» в 2011 году

Международный конкурс-игра «Кенгуру-2011»

Исследовательская работа «Золотое сечение вокруг нас» в рамках IV научно-практической конференции МОБУ СОШ № 35

Модель системы работы по развитию математических способностей учащихся во внеурочной деятельности Учащиеся с устойчивым интересом к предмету математики, но не имеющие достаточной подготовки.Учащиеся с устойчивой мотивацией к предмету, готовые решать задачи достаточной сложностиУчащиеся, владеющие рефлексивными навыками в изучении математики

Графы и их применение

продолжит разбирать задачи на построение графовприступит к рассмотрению задач с практическим применением графовзаймется исследовательской работой по данной теме

Требования к учителю, работающему с одаренными детьми: