Презентация на тему: Загадочное число ПИ

Городское управление образования г.ПолысаевоИнформационно-методический центрМуниципальное общеобразовательное учреждение«Средняя общеобразовательная школа № 35» Загадочное число ПИ Работа на городскую научно-исследовательскуюконференцию «Шаг в будущее» Выполнил:Олейник Юля,ученица 10 А классаРуководитель:Третьякова Галина Валерьяновна,учитель математики,Луцык Наталья Анатольевна,учитель информатики

Исследование природы числа ПИ и выявление его роли в окружающем нас мире.

ситуации возникновения числа .трансцендентность числа .некоторые способы вычисления числа .проблему квадратуры круга. 2. Провести собственный опыт исследования по вычислению числа ПИ. 3. Раскрыть загадочность числа ПИ.

Первое знакомство с числом ПИ Длина окружности: Площадь круга

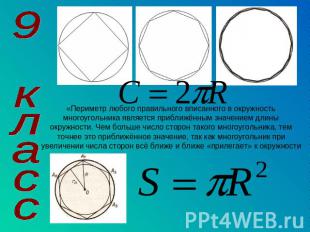
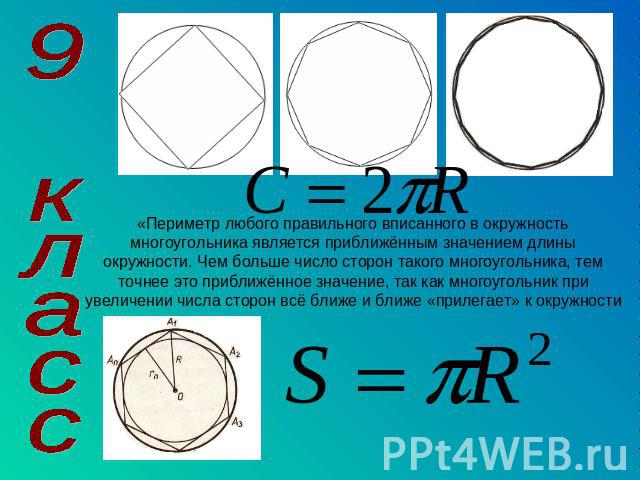
«Периметр любого правильного вписанного в окружность многоугольника является приближённым значением длины окружности. Чем больше число сторон такого многоугольника, тем точнее это приближённое значение, так как многоугольник при увеличении числа сторон всё ближе и ближе «прилегает» к окружности 9 класс

Особое значение число имеет в курсе «Алгебры и начала анализа» в 10 классе для измерения угла в радианах, при изучении темы «Тригонометрические функции».

Математический ребус на тему числа ПИ Разгадав ребус, вы узнаете имя древнегреческого философа и математика, которому приписывают открытие важнейших теорем геометрии.

На этом школьная жизнь числа не заканчивается. В старших классах мы встречаемся с этим удивительным числом в курсе физики на таких темах как:1. Движение тела по окружности: Физика

Возникновение числа ПИ 1. Рассмотрим множество положительных чисел. Если у них случайным образом выбрать два числа, то какова вероятность того, что выбранные числа не будут иметь общего делителя? Ответ неожидан: искомая вероятность равна:

2. Когда-то немецкий математик Лейбниц (1646-1716) заинтересовался, сколько получится в пределе, если последовательно будем складывать такие числа: Оказалось, что в пределе мы получим . (Для доказательства Лейбниц пользовался приёмами высшей математики).

3. Аналогичный вопрос поставил перед собой Леонар Эйлер. Его интересовала «сумма чисел: ». Число участвует и в известной формуле Эйлера из которой ещё глубже выясняется природа числа . Полученные формулы для числа позволяют вычислить это число с большой точностью, не обращаясь к окружности и правильном многоугольникам, и при этом значительно легче и быстрее.

4. Было найдено и много других формул, где неожиданно появляется число . Вот формула английского математика Джона Валлиса: 5. Удобнее для вычислений ряд, получаемый разложением при Наилучшую формулу для вычисления числа получил Дж. Мэчан, пользуясь также разложением в ряды . Он вычислил с точностью до 100 десятичных знаков.6. Число встречается и в некоторых формулах неевклидовой геометрии, где оно, конечно, не является отношением длины окружности к её диаметру, а определяется число аналитически.

Трансцендентность числа ПИ По определению трансцендентным называют число, которое не является корнем никакого алгебраического уравнения с рациональными коэффициентами.

Вычисления значений числа ПИ В Древнем Египте при вычислении площади круга для использовали значение 2. Древнеримский архитектор Витрувий принимал 3. Архимед нашёл более точное приближение для числа . Он показал, что так что

Числовой фокус китайского астронома Цю Шунь-Ши Напишем по два раза три нечётных числа: 1, 1, 3, 3, 5, 5. Три последних числа сделаем числителем, а три первых – знаменателем дроби . Эта дробь позволяет вычислить с точностью до седьмого знака.

Чтобы вычислить приближенно число ПИ, в течение многих столетий поступали так: в окружность с диаметром, равным единице, мысленно вписывали правильный многоугольник с большим числом сторон и вычисляли периметр этого многоугольника, привлекая «формулу удвоения». Периметр такого многоугольника и принимался равным числу . Для оценки погрешности такого приближения приходилось рассматривать также периметры правильных описанных многоугольников

Проблема квадратуры круга Можно ли, пользуясь только циркулем и линейкой, построить квадрат, площадь которого была бы в точности равна площади данного круга?

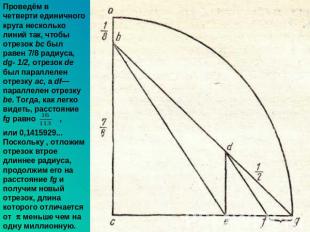
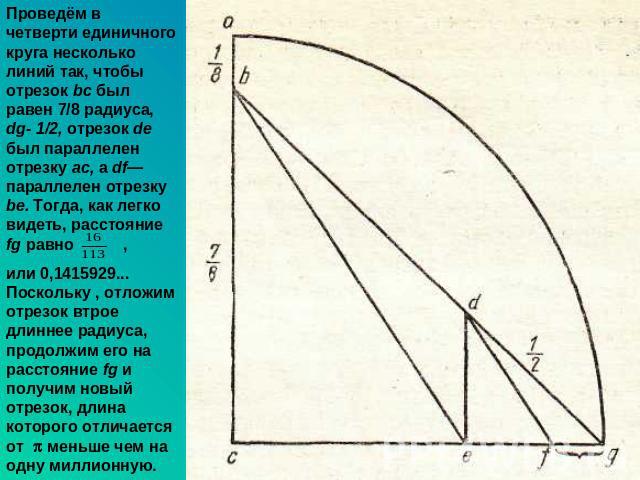
Проведём в четверти единичного круга несколько линий так, чтобы отрезок bc был равен 7/8 радиуса, dg- 1/2, отрезок de был параллелен отрезку ас, a df— параллелен отрезку be. Тогда, как легко видеть, расстояние fg равно , или 0,1415929... Поскольку , отложим отрезок втрое длиннее радиуса, продолжим его на расстояние fg и получим новый отрезок, длина которого отличается от меньше чем на одну миллионную.

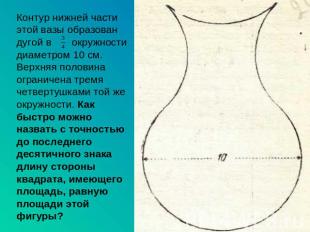
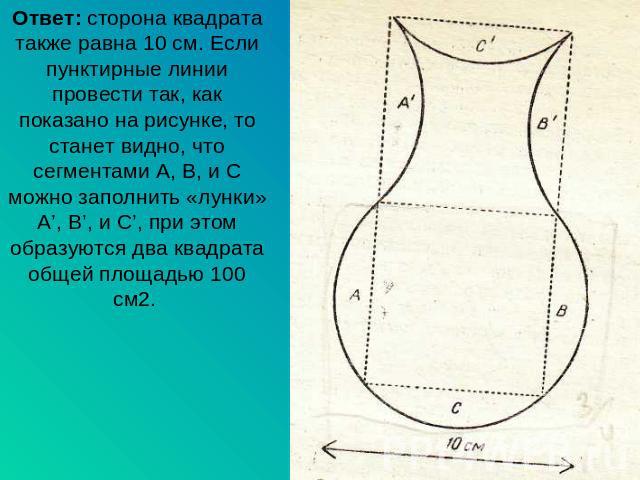
Контур нижней части этой вазы образован дугой в окружности диаметром 10 см. Верхняя половина ограничена тремячетвертушками той же окружности. Как быстро можно назвать с точностью до последнего десятичного знака длину стороны квадрата, имеющего площадь, равную площади этой фигуры?

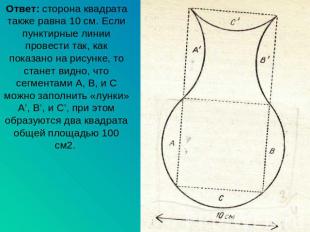
Ответ: сторона квадрата также равна 10 см. Если пунктирные линии провести так, как показано на рисунке, то станет видно, что сегментами A, B, и C можно заполнить «лунки» A’, B’, и C’, при этом образуются два квадрата общей площадью 100 см2.

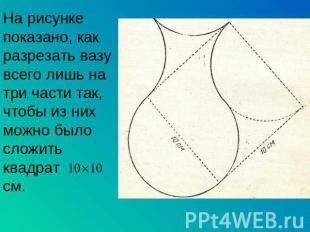
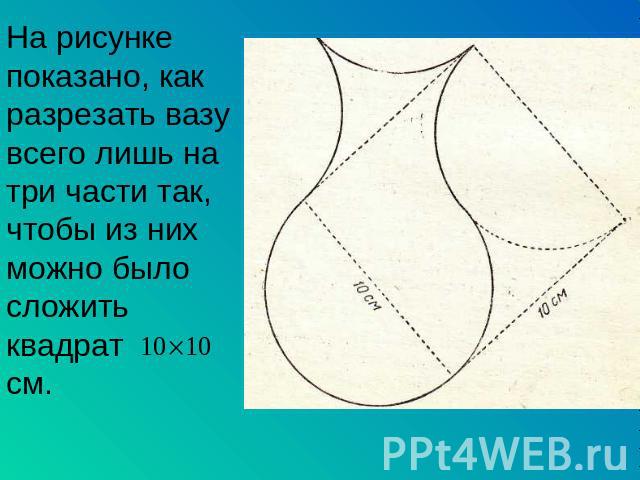
На рисунке показано, как разрезать вазу всего лишь на три части так, чтобы из них можно было сложить квадрат см.

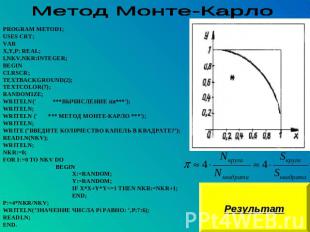
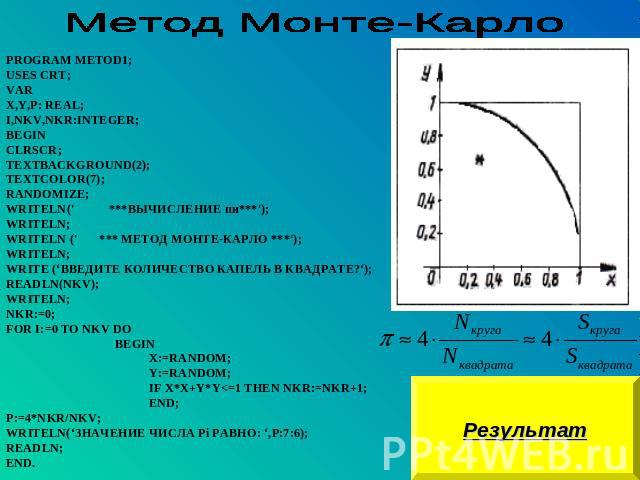
Метод Монте-Карло PROGRAM METOD1;USES CRT;VAR X,Y,P: REAL; I,NKV,NKR:INTEGER;BEGIN CLRSCR;TEXTBACKGROUND(2);TEXTCOLOR(7);RANDOMIZE;WRITELN(' ***ВЫЧИСЛЕНИЕ пи***');WRITELN;WRITELN (' *** МЕТОД МОНТЕ-КАРЛО ***');WRITELN;WRITE (‘ВВЕДИТЕ КОЛИЧЕСТВО КАПЕЛЬ В КВАДРАТЕ?‘);READLN(NKV);WRITELN;NKR:=0;FOR I:=0 TO NKV DO BEGIN X:=RANDOM; Y:=RANDOM; IF X*X+Y*Y<=1 THEN NKR:=NKR+1; END;P:=4*NKR/NKV;WRITELN(‘ЗНАЧЕНИЕ ЧИСЛА Pi РАВНО: ‘,P:7:6);READLN;END.

Метод Прямоугольников ROGRAM METOD2;USES CRT;VAR F, DX, P, X, A: REAL; I, N:INTEGER;BEGIN CLRSCR;TEXTBACKGROUND(2);TEXTCOLOR(7);WRITELN(' ***ВЫЧИСЛЕНИЕ пи***');WRITELN;WRITELN (' *** МЕТОД ПРЯМОУГОЛЬНИКОВ ***');WRITELN;WRITE (‘ВВЕДИТЕ КОЛИЧЕСТВО ТОЧЕК ДЕЛЕНИЯ ОТРЕЗКА? ‘);READLN(N);WRITELN;DX:=1/N;FOR I:=0 TO N-1 DO BEGIN F:=SQRT(1-SQR(X)); X:=X+DX; A:=A+F; END;P:=4*DX*A;WRITELN(‘ЗНАЧЕНИЕ ЧИСЛА Pi РАВНО: ‘,P:7:6);READLN;END.

Метод Тейлора ROGRAM METOD3;USES CRT;VAR S, P, F: REAL; I, N:INTEGER;BEGIN CLRSCR;TEXTBACKGROUND(2);TEXTCOLOR(7);WRITELN(' ***ВЫЧИСЛЕНИЕ пи***');WRITELN;WRITELN (' *** МЕТОД ПРЯМОУГОЛЬНИКОВ ***');WRITELN;WRITE (‘ВВЕДИТЕ КОЛИЧЕСТВО ЧЛЕНОВ РЯДА ТЕЙЛОРА? ‘);READLN(N);WRITELN;S:=1;FOR I:=1 TO N DO BEGIN F:=1/(2*I+1); IF I MOD 2=0 THEN F:=F ELSE F:=-F; S:=S+F; END;P:=4*S;WRITELN(‘ЗНАЧЕНИЕ ЧИСЛА Pi РАВНО: ‘,P:7:6);READLN;END.

Свои данные исследования я занесла в следующую таблицу: Вывод: во всех методах вычисления - чем больше значение N (либо – количество капель в квадрате, либо – количество членов ряда Тейлора, либо – количество точек деления отрезка), тем более точнее вычисляется приближённое значение числа . Из всех трёх методов более точнее работает метод Тейлора

Метод "Падающей иголки" Я взяла обыкновенную швейную иголку и лист бумаги. На листе провела несколько параллельных прямых так, чтобы расстояние между ними были равны и совпадали с длиной иголки. Чертёж должен быть достаточно большим, чтобы случайно брошенная игла не упала за его пределами. На этот лист я бросала сверху иглу и подсчитывала, сколько раз при данном числе бросаний игла пересечёт одну из параллелей (безразлично какую).

Свои результаты я занесла в таблицу: Вывод: оказалось, что при большем числе бросаний (n) дробь и это равенство будет тем точнее, чем больше будет число бросаний.

Число ПИ - разумно Идеальная дата рождениячисла ПИ 14 марта 1592 года(3,141592) Альберт Эйнштейн 14 марта 1879 года

Вадим Косогоров: «Почему, зная о нежелании числа ПИ быть опознанным в качестве разумного, я не побоялся прийти сюда и вам всё это рассказать? Да потому, что для меня это и был единственный способ выжить. Теперь-то ПИ придётся или убить всех вас, или смириться с тем, что его тайна раскрыта. Будем надеяться, что Оно поступит разумно»

Спасибоза внимание!