Презентация на тему: Загадки круга

Загадки круга

Цель работы исследование зависимости между радиусом, длиной окружности и площадью круга. Задачи: Систематизировать теоретические сведения о круге и окружности в школьном курсе математики.Исследовать изменение длины окружности и площади круга в зависимости от изменения длины радиуса.Изучить историю вопроса.Показать применение материалов исследований при решении задач, в том числе задач с практическим содержанием, математических парадоксов.

Методы Работа с учебной и научно-популярной литературой.Социологический опрос:82человека; 33ученика 9-10кл.; 33родителя; 16 учителей.Наблюдение, сравнение, анализ, аналогия.Доказательство выдвинутых гипотез. Решение задач нестандартными способами.

Актуальность. Практическая направленность.Богатая история вопроса.Продолжение предыдущих исследований.

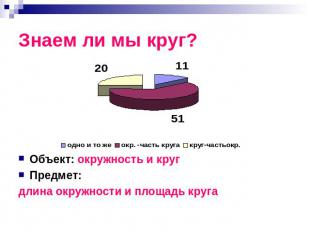
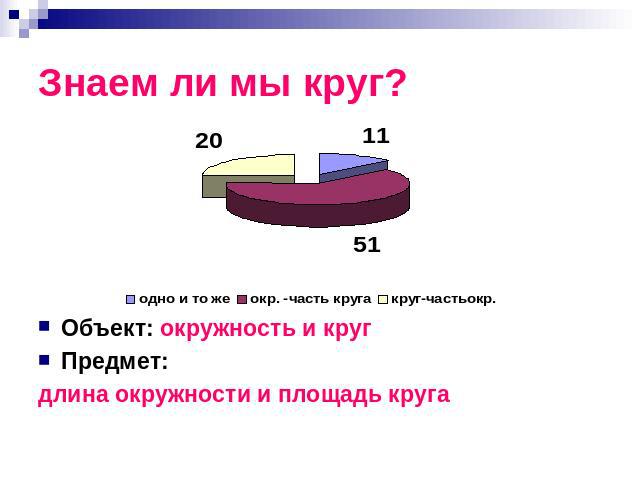
Знаем ли мы круг? Объект: окружность и кругПредмет: длина окружности и площадь круга

Теоретические сведенияОкружность Круг

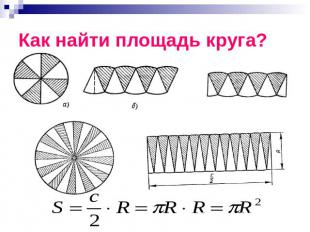
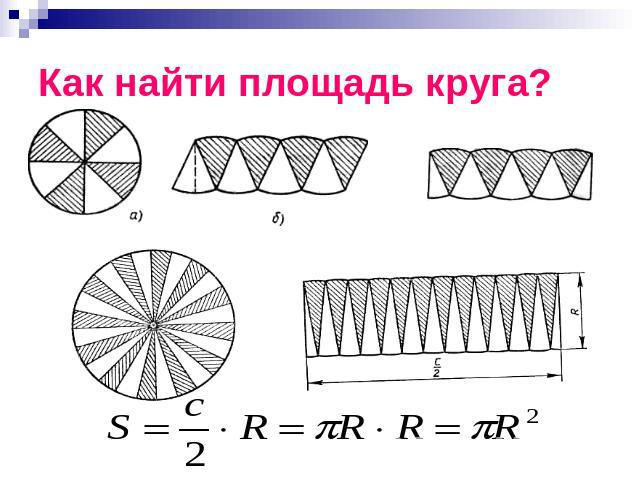
Как найти площадь круга?

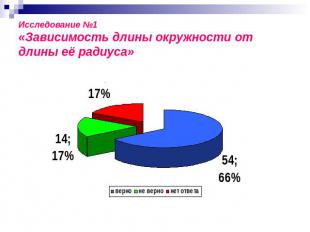
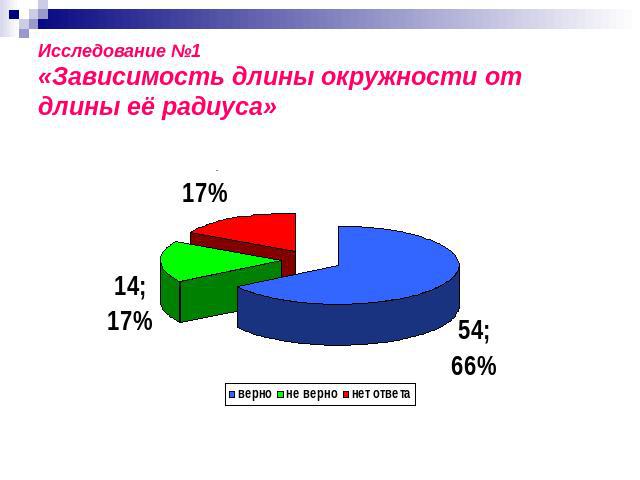
Исследование №1«Зависимость длины окружности от длины её радиуса»

Исследование №1«Зависимость длины окружности от длины её радиуса» при изменении (увеличении или уменьшении) радиуса окружности в раз её длина изменяется (увеличивается или уменьшается) также в раз.длина окружности пропорциональна её радиусу.

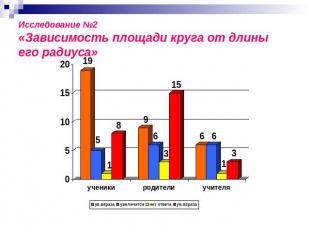
Исследование №2«Зависимость площади круга от длины его радиуса»

Исследование №2«Зависимость площади круга от длины его радиуса» при изменении (увеличении или уменьшении) радиуса круга в раз его площадь изменяется (увеличивается или уменьшается) в раз.площадь круга пропорциональна квадрату его радиуса.

Исследование №3«Максимальная площадь при заданном периметре» При заданном периметре круг ограничивает большую площадь, чем квадрат.При заданном периметре именно круг ограничивает максимальную площадь по сравнению с любыми другими фигурами.

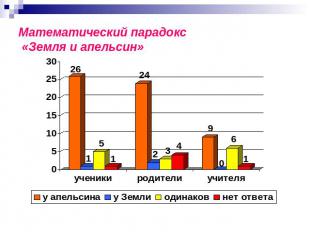
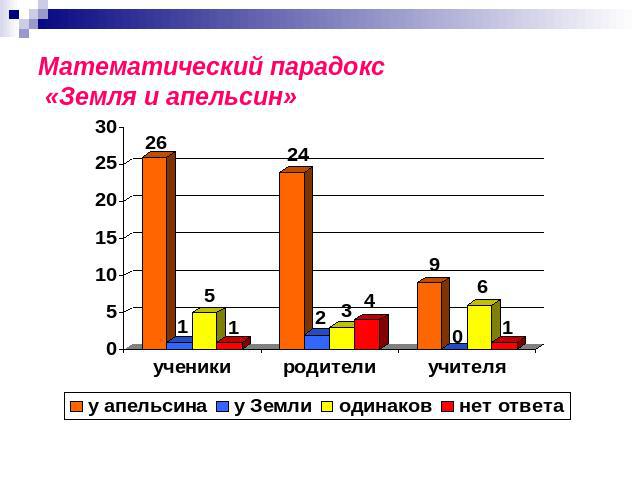
Математический парадокс «Земля и апельсин»

Исследование №4«Изменение радиуса при изменении длины окружности» Расстояние между концентрическими окружностями зависит только от разности длин этих окружностей (а) и не зависит от длины радиуса (R)

Решение задач 5-6класс Задача №1 (№866,Виленкин)Длина окружности 1,2 м. Чему равна длина другой окружности, у которой диаметр в 2 раза больше диаметра первой окружности?Ответ:2,4метра (Смотри исследование №1!)Задача №2(№867,Виленкин)Найдите площадь круга, у которого радиус 8 см. Найдите площадь второго круга, у которого радиус составляет радиуса первого круга.Ответ:48см2; 36см2 (Смотри исследование №2!)Задача №3 «Две клумбы» (№95.8, учебник-собеседник)Отец Вали и Веры предложил девочкам сделать две клумбы. Он дал им верёвку длиной 6м, чтобы с её помощью наметить границу каждой клумбы. Валя решила сделать клумбу квадратной, а Вера – круглой. Чья клумба будет иметь большую площадь? Радиус круглой клумбы вычислите с точностью до сотых. Во сколько раз площадь одной клумбы будет больше площади другой?Ответ: площадь круглой клумбы будет примерно в 1, 28 раза больше, чем квадратной (радиус 0,96м) (Смотри исследование №3!)

Решение задач 9класса, из дополнительной литературы Задача №1№1102(Атанасян)Как изменится длина окружности, если радиус окружности:а)увеличить в 3 раза; б)уменьшить в 2 раза; в) увеличить в раз; г) уменьшить в раз?Ответ: увеличится в 3 раза, уменьшится в 2 раза, увеличится в раз; уменьшится в раз (смотри исследование №1).Задача №2 «Земной шар и мышь»Если обтянуть земной шар по экватору проволокой и затем прибавить к её длине 1м, то сможет ли между проволокой и землёй проскочить мышь?Ответ: даРешение.Обычно отвечают, что промежуток будет тоньше волоса: что значит прибавка в один метр по сравнению с 40 миллионами метров земного экватора! В действительности же величина промежутка равна . Не только мышь, но и крупный кот проскочит в такой промежуток!!! (смотри исследование №4).

История числа «ПИ» 3,141592653589793238462643383279… Это я знаю и помню прекрасно:"Пи" многие знаки мне лишни, напрасны.Нужно только постараться И запомнить все, как есть: Три, четырнадцать, пятнадцать, Девяносто два и шесть.

Архимед Уж, пыль клубится над дорогой, То в рабство путь, в ярмо цепей.«Убей меня, но лишь не трогай,О, варвар, этих чертежей!»Прошли столетий вереницы,Научный подвиг не забыт.Никто не знает, кто убийца,Но знают все, кто был убит!

Квадратура круга – синоним неразрешимости1.Квадратура круга2.Трисекция угла3.Удвоение куба.

Загадки: разгаданные и неразгаданные ЗАГАДКИ КРУГА(увлекательные задачи по теме «Длина окружности и площадь круга»для любознательных шестиклассников и не только…)