Презентация на тему: Загадки ленты мёбиуса

ЗАГАДКИЛЕНТЫ МЁБИУСА

Лист Мёбиуса – желтая страница, Односторонний сказочный маршрут, Летит метелью, песенкой, синицей, Бульварной лентой, склеенный лоскут.Эх, Мёбиус, спасибо за науку! Поверхность одинокой стороны Подобна закольцованному звуку, Вибрацией неоновой струны.

Содержание ВведениеЦель работыЛист МебиусаТопологияОпытыСюрпризы ленты МебиусаПрименениеВыводыСписок литературы

У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная на полвитка. В 1967 году в Бразилии состоялся международный математический конгресс.

Его устроители выпустили памятную марку достоинством в пять сентаво. На ней была изображена лента Мёбиуса. И монумент высотой более чем в два метра, и крохотная марка – своеобразные памятники немецкому математику и астроному Августу Фердинанду Мёбиусу, профессору Лейпцигского университета.

Познакомиться с историей возникновения ленты МебиусаИсследовать свойства ленты МебиусаИсследовать применение ленты Мебиуса в жизниПознакомиться с технологией работы, Macromedia Flash, Adobe Photoshop.Продолжить работу в Microsoft Power Point.

Таинственный и знаменитый лист Мёбиуса придумал в 1858 году немецкий геометр Август Фернанд Мебиус (1790 - 1868), ученик «короля математиков» Гаусса. Мёбиус был первоначально астрономом, как Гаусс и многие другие из тех, кому математика обязана своим развитием.

В те времена занятия математикой не встречали поддержки, а астрономия давала достаточно денег, чтобы не думать о них, и оставляло время для собственных размышлений. И Мёбиус стал одни из крупнейших геометров XIX века. В возрасте 68 лет ему удалось сделать открытие поразительной красоты.

Идея пришла ему в голову, когда служанка неправильно сшила ленту.

Лист Мёбиуса - поверхность, получающаяся при склеивании двух противоположных сторон AB и А`В` прямоугольника ABB`A` так, что точки А и В совмещаются соответственно с точками B` и A`.

Лист Мёбиуса - топологический объект, простейшая односторонняя поверхность с краем. Сама топология началась именно с листа Мёбиуса. Слово это придумал Иоганн Бенедикт Листинг, который почти в тоже время, что и его коллега, предложил в качестве первого примера односторонней поверхности уже знакомую нам перекрученную ленту.

Топология известна и под именем «резиновая гео-метрия», потому что топологу ничего не стоит поместить все свои фигуры на поверхность детского надувного шарика и без конца менять его форму, следя лишь за тем, чтобы шарик не лопнул. А то, что при этом прямые линии, например стороны треугольника, пре-вратятся в кривые, для то-полога глубоко безразлично.

Любую фигуру тополог имеет право сгибать, скручивать, сжимать и растягивать – делать с ней всё что угодно, только не разрывать и не склеивать. И при этом он будет считать, что ничего не произошло, все её свойства остались неизменными. Для него не имеют никакого значения ни расстояния, ни углы, ни площади.

Взгляните с этой точки зрения на нашего старого знакомца и увидите: на листе Мёбиуса любая точка может быть соединена с любой другой точкой и при этом муравью на гравюре Эшера ни разу не придётся переползать через край «ленты». Разрывов нет – непрерывность полная.

Опыт №1Раскрасим внутреннюю и внешнюю сторону обычного кольца разными красками.Попробуем раскрасить ленту Мебиуса.Вывод: «Если кто-нибудь вздумает раскрасить только одну сторону поверхности мёбиусовой ленты, пусть сразу погрузит её всю в ведро с краской», - пишет Рихард Курант и Герберт Робинс в превосходной книге «Что такое математика?»Лента Мебиуса – односторонняя поверхность.

Опыт №2На внутреннюю сторону обычного кольца посадим зайца, а на наружную волка. Разрешили бегать как угодно, запретив перелезать через края кольца. Вывод: они не встретятся; каждый пробежит только одну, «свою» сторону кольца.

Опыты Опыт №3. Посадим на ленту Мебиуса зайца и волка. Разрешим им бежать в разных направлениях.Вывод: заяц и волк столкнулись! Лента Мебиуса – односторонняя поверхность.

Опыт №4Этой поразительной особенностью не исчерпываются свойства ленты Мебиуса. Попробуем закрасить узенькую полоску ее края.Вывод: у ленты Мебиуса не только одна сторона, но и только один край!

Сюрпризы ленты Мебиуса Лента Мёбиуса преподнесет нам не один сюрприз, если вы попытаетесь ее разрезать. Разделим ленту пополам, разрезая её посередине по линии, параллельной краю. Вместо двух лент получится одна длинная лента с двумя полуоборотами (не лента Мёбиуса).

Сюрпризы ленты Мебиуса Если теперь эту ленту разрезать посередине, то получаются две ленты намотанные друг на друга. Если же разрезать ленту Мёбиуса, отступая от края приблизительно на треть её ширины, то получаются две ленты, одна — более тонкая лента Мёбиуса, другая — длинная лента с двумя полуоборотами (не лента Мёбиуса).

Лента Мебиуса понравилась не только математикам, но и фокусникам.Более 100 лет лента Мёбиуса используется для показа различных фокусов и развлечений. Удивительные свойства листа демонстрировались даже в цирке, где подвешивались яркие ленты, склеенные в виде листов Мёбиуса.

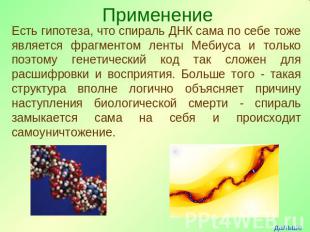
Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того - такая структура вполне логично объясняет причину наступления биологической смерти - спираль замыкается сама на себя и происходит самоуничтожение.

В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса. В 1971 году изобретатель с Урала Чесноков П.Н. применил фильтр в виде листа Мёбиуса. И это только ничтожная часть примеров использования этой удивительной поверхности.

Применение Фотографии образцов конструкций, использующих лист Мёбиуса Силовая конструкция (квадратная), мешалка (большая круглая), винты, испытывающиеся на модели судна (два маленьких круглых)

Применение Трансформатор

Мотив Ленты Мебиуса встречается в названиях художественных произведений, общественных заведений, логотипах. Инженерно- производственная фирма Мебиус книга Ресторан «Лента Мебиуса» Международный символ переработки

Лента Мебиуса вдохновила многих художников на создание известных скульптур, картин и для графического искусства .

Лист Мебиуса имеет один край.Лист Мебиуса имеет одну сторону.Лист Мёбиуса - топологический объект. Как и любая топологическая фигура лепта Мёбиуса не меняет своих свойств, пока ее не разрезают, не разрывают или не склеивают его отдельные куски.Один край и одна сторона листа Мебиуса не связаны с его положением в пространстве, не связаны с понятиями расстояния.

Лист Мёбиуса находит многочисленные применения в науке, технике и изучении свойств Вселенной.Лента Мебиуса вдохновляет многих художников на создание известных скульптур и картин.Чудесные свойства ленты порождают множество научных трудов, изобретений (весьма полезных и совершенно нереальных), а также множество фантастических рассказов.

1. М.Гарднер «Математические чудеса и тайны»«Наука» 1978 г.2. Е.С. Смирнова «Курс наглядной геометрии» 6 класс.«Просвещение» 2002 г.3. И.Ф. Шарыгин . Л.Н. Еранжиева «Наглядная геометрия» 5-6 класс.«Дрофа» 2000г.4. Энциклопедия для детей «Математика». «Аванта+»2001г.Материалы сайтов:http://arbuz.uz/t_lenta.htmlhttp://www.frei.ru/golos/books/http://umiranie.chat.ru/sphere.htmhttp://school-sector.relarn.ru/dckt/projects/ctrana/matric/t_lm1.htmhttp://www.kvant.info/http://www.websib.ru/noos/math/listmebiusa/