Презентация на тему: Числовая последовательность

В науке о числах… надо ожидать весьма многого от наблюдений, ибо они постоянно приводят нас к новым свойствам, над доказательством которых приходится работать. Л. Эйлер Тема учебного проекта: «Числовая последовательность» ( 9 класс) Автор проекта: ученица 9 б класса МОУ «Никифоровская СОШ №1» Тамбовской области Миронова Оксана Руководитель проекта: учитель математики Муравьева Инна Николаевна ©Миронова О, 2008

Цель исследования. Установив закономерность ряда Фибоначчи, исследовать его интересные свойства. Задачи исследования.Рассмотреть рекуррентную формулу ряда Фибоначчи.Найти связь с «золотым сечением». Экспериментально убедиться в существовании чисел Фибоначчи в природе, истории человечества.Научиться пользоваться PowerPoint для оформления результатов.Учебные предметы: математика , биология, история.

Гипотеза. Если такая закономерность чисел существует, то она должна проявляться в законах природы и хронологии истории.

Ход исследования. В одной из математических книг я встретила задачу итальянского математика Леонардо Фибоначчи. Некто посадил пару кроликов в загон, окружённый со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару? Фибоначчи (ок.1175-1250)

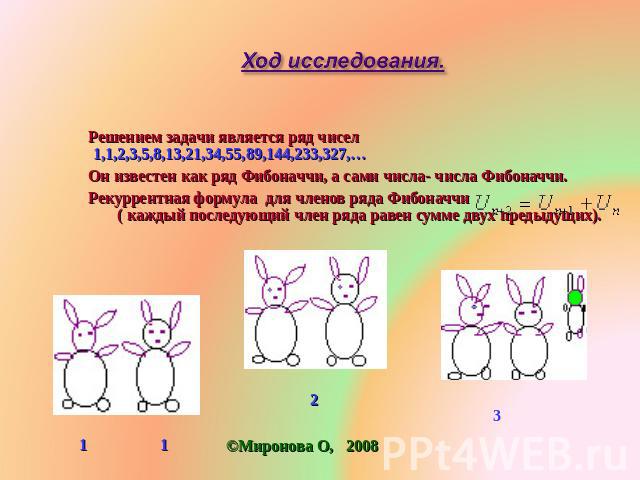
Ход исследования. Решением задачи является ряд чисел 1,1,2,3,5,8,13,21,34,55,89,144,233,327,… Он известен как ряд Фибоначчи, а сами числа- числа Фибоначчи. Рекуррентная формула для членов ряда Фибоначчи ( каждый последующий член ряда равен сумме двух предыдущих).

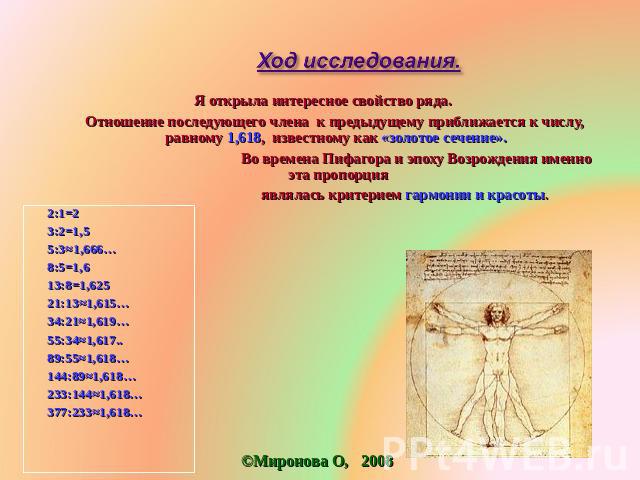
Ход исследования. Я открыла интересное свойство ряда. Отношение последующего члена к предыдущему приближается к числу, равному 1,618, известному как «золотое сечение». Во времена Пифагора и эпоху Возрождения именно эта пропорция являлась критерием гармонии и красоты.2:1=2 3:2=1,55:3≈1,666…8:5=1,613:8=1,62521:13≈1,615…34:21≈1,619… 55:34≈1,617..89:55≈1,618…144:89≈1,618…233:144≈1,618…377:233≈1,618…

Я рассмотрела семена на корзинках подсолнечников. Они образуют сложный рисунок пересекающихся спиралей, которые закручиваются как слева направо, так и справа налево. Подсчёты показали, что если в одну сторону закручено 13 спиралей, то в другую 21. В более крупных соцветиях подсолнечника число спиралей соответственно 21 и 34 или 34 и 55. Обратите внимание эти числа в ряду Фибоначчи стоят рядом.

Ход исследования . Исследования проводились на растениях : диффенбахия и фикус. Оказалось, что расстояния между листьями неодинаковы. В 75% опытов они пропорциональны числам ряда Фибоначчи:1,2,3,5,8,13… Это явление в ботанике получило название «филлотаксиса» (листорасположение).

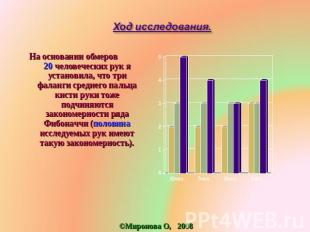
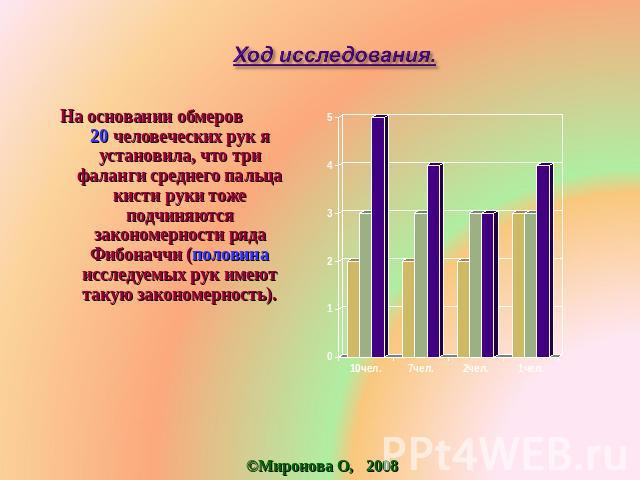
Ход исследования. На основании обмеров 20 человеческих рук я установила, что три фаланги среднего пальца кисти руки тоже подчиняются закономерности ряда Фибоначчи (половина исследуемых рук имеют такую закономерность).

Ход исследования. Исследуя хронологию развития человечества с древних времён до начала современной эпохи, я увидела возможность использования ряда Фибоначчи в разработке периодизации. До нашей эры (тыс.лет) Соответствия периодов истории и чисел Фибоначчи проверены и подтверждены с достаточной степенью надёжности и точности (61% совпадений).

Выводы. Полученные результаты исследований дают возможность утверждать, что в природе с достаточным постоянством повторяются числа Фибоначчи.Может быть, эти загадочные числа ведут нас к разгадке великой тайны-Тайны Жизни? Эта загадка- тема моих будущих исследований.

Информационные ресурсы. 1. Воробьёв Н.Н. Числа Фибоначчи. -М.: Наука,1969.2. Виленкин Н.Я. И др. Комбинаторика.- М. :ФИМА, МЦНМО, 2006.3. Васютинский Н.А. Золотая пропорция.- М., Молодая гвардия,1990.4. Большая энциклопедия Кирилла и Мефодия ( БЭКМ), 2004.5. http:// www.google.com6. http:// www.exponenta.ru7. http:// www.1september.ru