Презентация на тему: Векторы

ВЕКТОРЫ

В Замечание: геометрически вектор изображается в виде направленного отрезка, т.е.указывается какая точка является началом, какая - концом Опр.: Векторная величина - это величина, которая характеризуется указанием направления и числового значения. М С Д Обозначение:

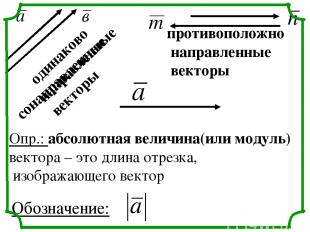
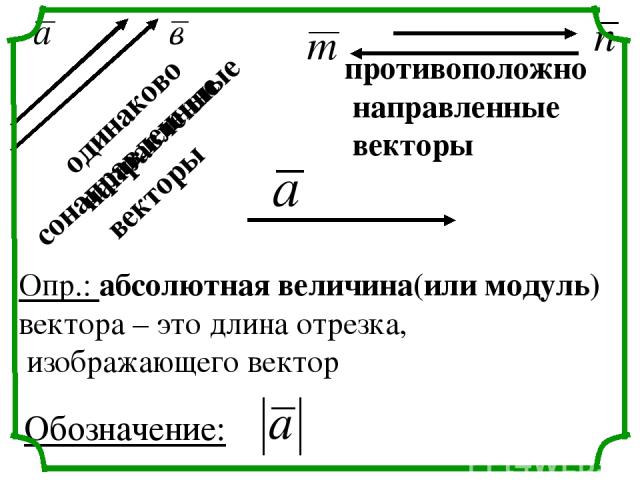
одинаково направленные векторы противоположно направленные векторы Опр.: абсолютная величина(или модуль) вектора – это длина отрезка, изображающего вектор Обозначение: сонаправленные

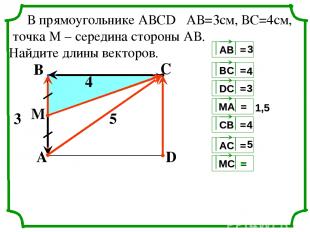
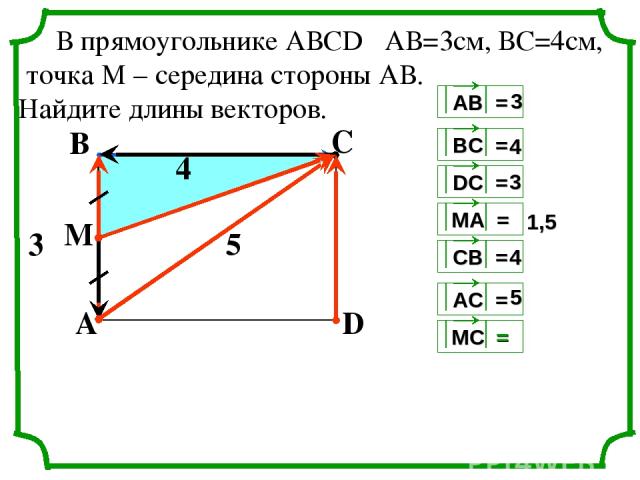
С А В D 4 3 4 3 1,5 4 5 5 M В прямоугольнике АВСD АВ=3см, ВС=4см, точка М – середина стороны АВ. Найдите длины векторов. 3

= Опр.: Равные векторы- векторые, которые сонаправлены и равны по абсолютной величине Свойство равных векторов: у равных векторов соответствующие координаты равны.

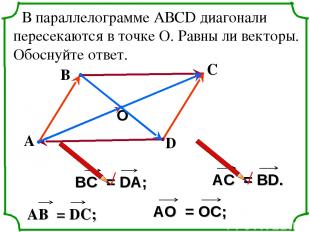
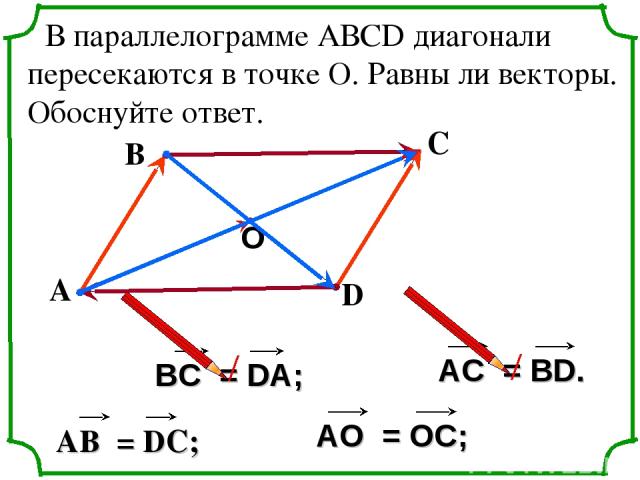
В параллелограмме АВСD диагонали пересекаются в точке О. Равны ли векторы. Обоснуйте ответ. А В С D

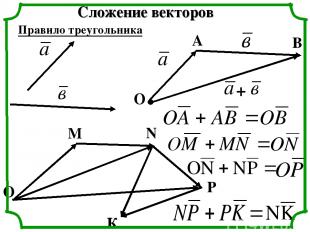
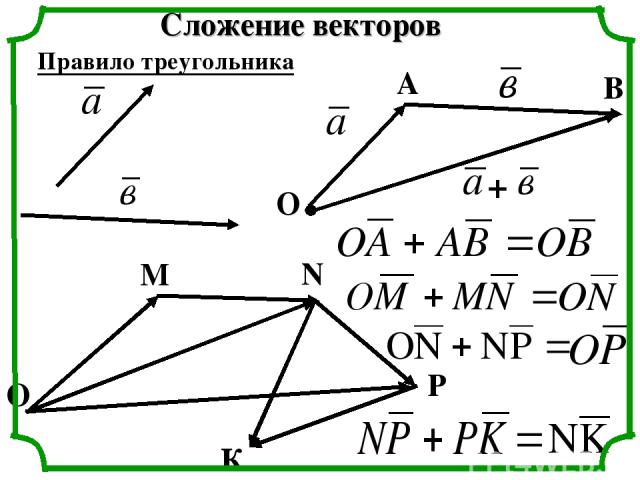
Сложение векторов Правило треугольника + О А В О М N Р К

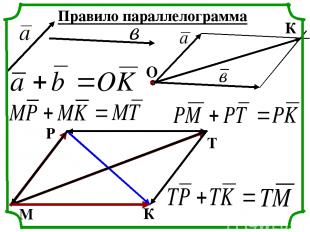
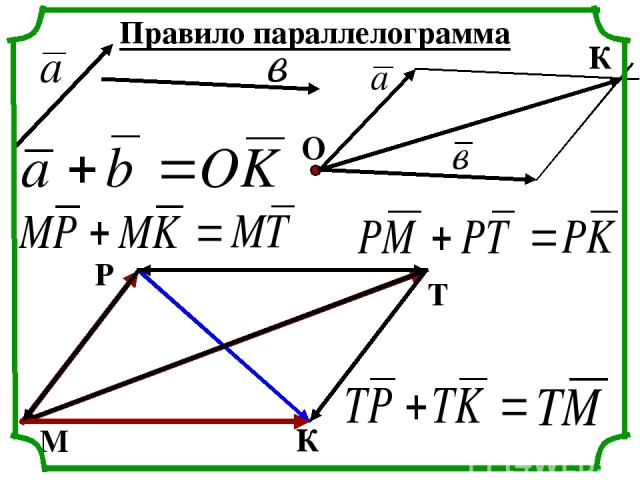
Правило параллелограмма О К М Р Т К

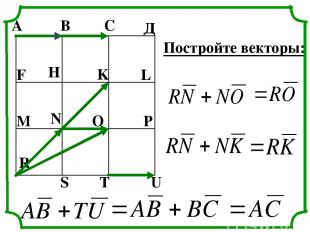
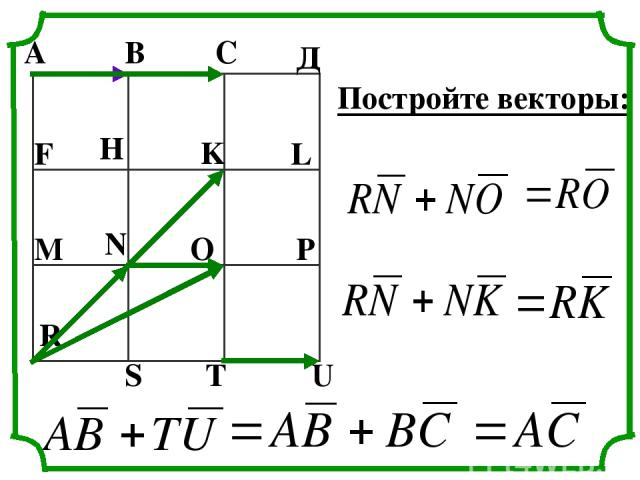
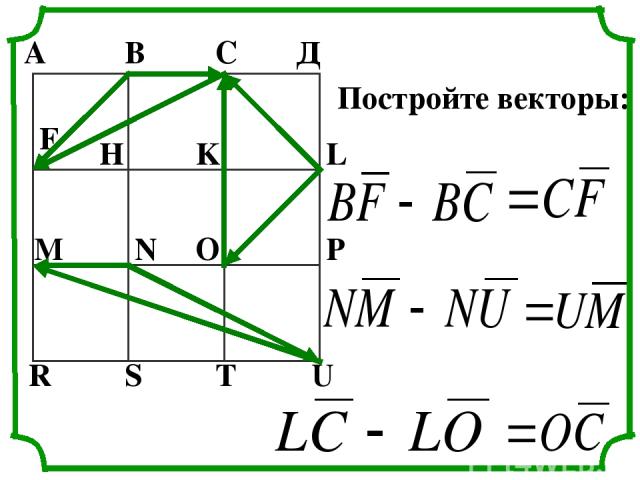
А В С Д F H K L M N O P R S T U Постройте векторы:

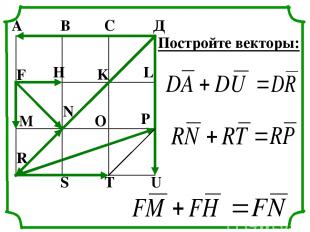
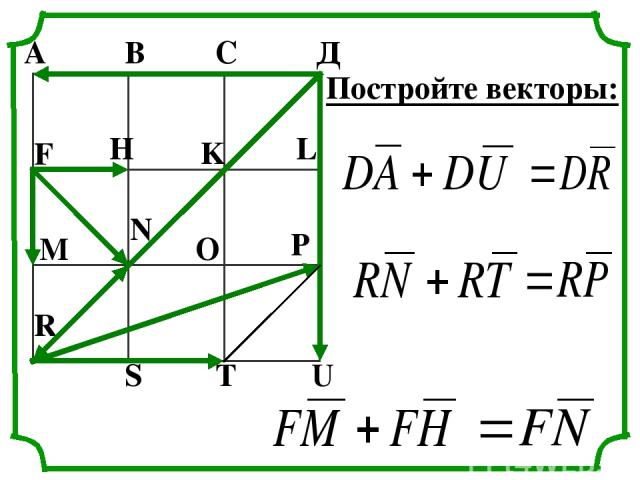
А В С Д F H K L M N O P R S T U Постройте векторы:

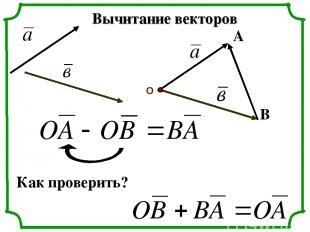
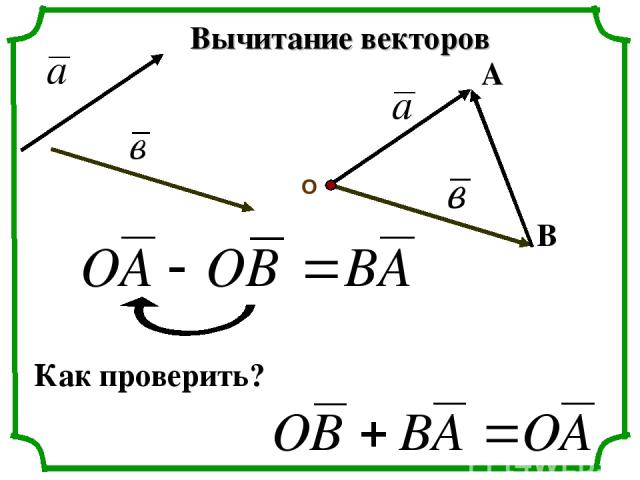
Вычитание векторов О А В Как проверить?

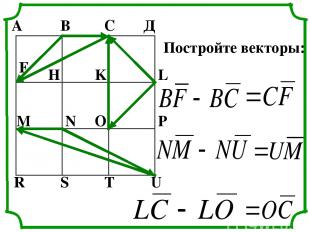
А В С Д F H K L M N O P R S T U Постройте векторы:

Умножение вектора на число О К и сонаправленные, если противоположно направленные, если

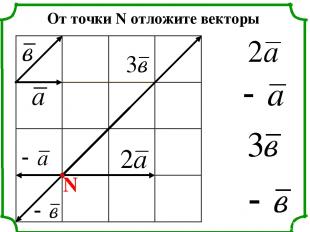
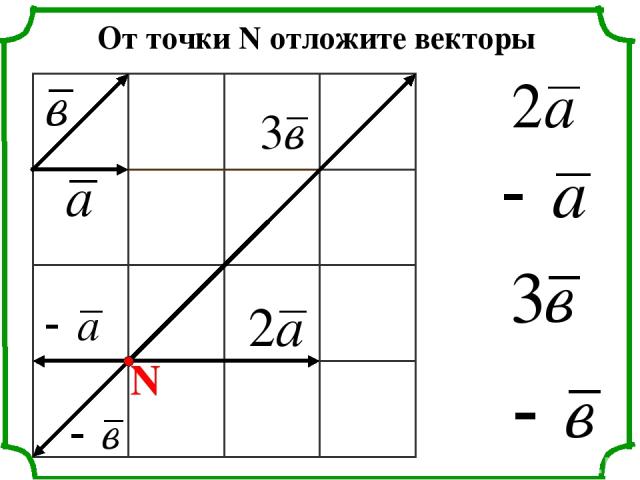
N От точки N отложите векторы

Опр.: Нулевой вектор - вектор, у которого начало совпадает с его концом. Замечание: любая точка плоскости является нулевым вектором.

Опр.:Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Замечания: а) коллинеарные векторы могут быть сонаправленными или противоположно направленными. б)Нулевой вектор считается коллинеарным любому вектору.

Свойство коллинеарных векторов: у коллинеарных векторов соответствующие координаты пропорциональны. Обратное утверждение является признаком коллинеарности векторов

Любой вектор можно разложить по двум неколлинеарным векторам и при этом коэффициенты разложения определяются единственным способом: Теорема. p=xa+yb

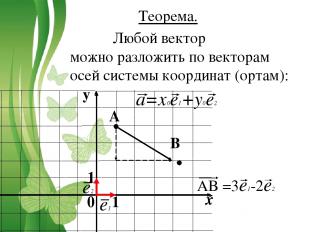
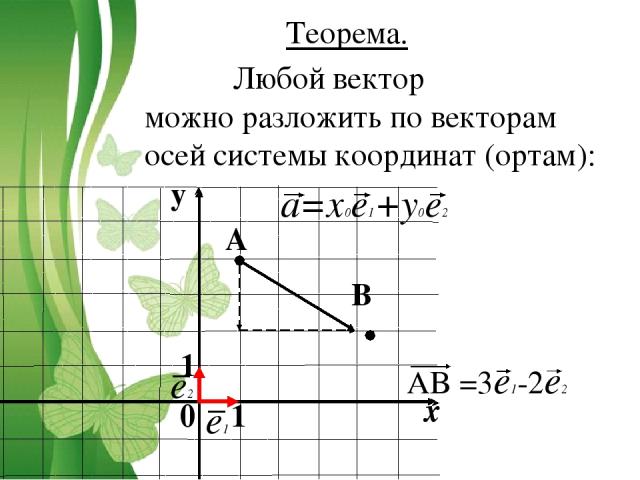
Теорема. Любой вектор можно разложить по векторам осей системы координат (ортам): a=x0e1+y0e2 0 1 1 A B e1 e2 AB =3e1-2e2

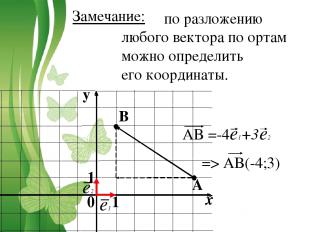
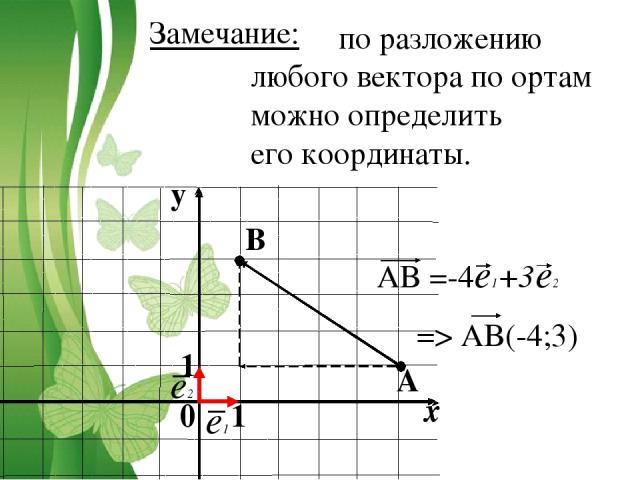
по разложению любого вектора по ортам можно определить его координаты. 0 1 1 A B e1 e2 AB =-4e1+3e2 Замечание: => AB(-4;3)

Опр.: Вектор b называется противоположным вектору а, если а и b имеют равные длины и противоположно направлены. Замечание: сумма противоположных векторов равна нулевому вектору.

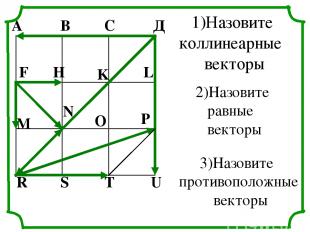
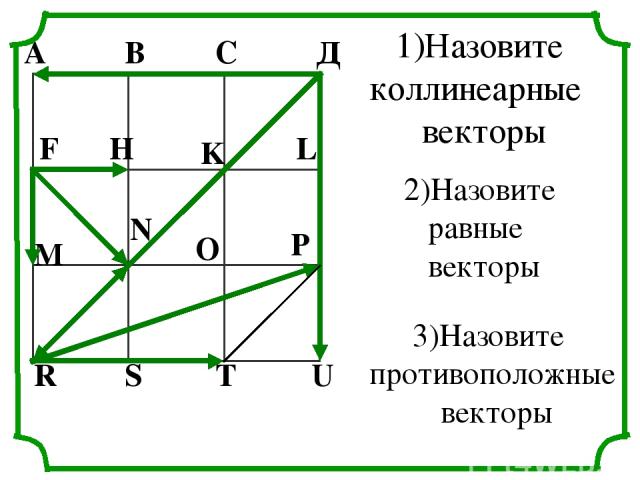
А В С Д F H K L M N O P R S T U 1)Назовите коллинеарные векторы 2)Назовите равные векторы 3)Назовите противоположные векторы

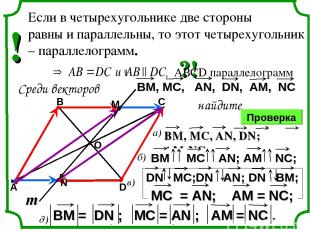
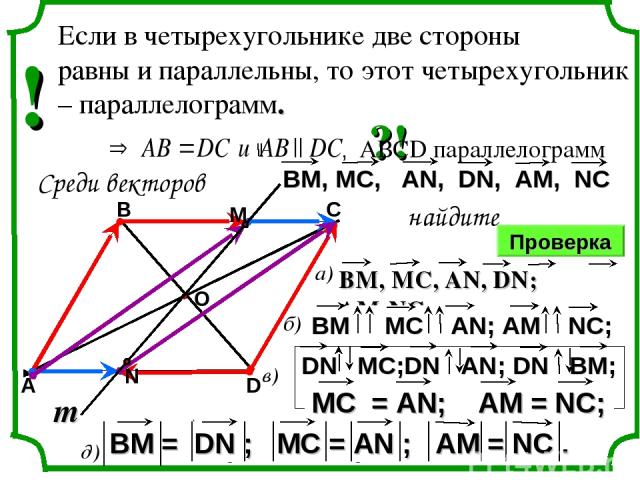
а) коллинеарные векторы; б) сонаправленные векторы; в) противоположные векторы; г) равные векторы; д) векторы, имеющие равные длины. В четырехугольнике АВСD , О – точка пересечения диагоналей. Прямая проходит через точку О и пересекает стороны ВС и АD в точках М и N соответственно. А В С D m ?! Среди векторов найдите , АВСD параллелограмм Проверка

А В С Опр.: СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ число равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение векторов Теорема: есть число равное сумме произведений соответствующих координат

Следствие 1. Следствие 2.

СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 1.Скалярное произведение сонаправленных векторов равно положительному произведению их длин. 2.Скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин.

3.Если скалярное произведение векторов равно нулю, то данные векторы перпендикулярны. Замечание: данное утверждение является признаком ортогональности векторов. 4.Скалярный квадрат вектора равен квадрату его абсолютной величины.