Презентация на тему: Урок одной задачи

Урок одной задачи Пентяшкина Татьяна Петровна учитель МБОУ ССОШ№1 Вольно-НадеждинскоеПриморский край

Задача С2 КИМ 5 июня 2013г. В прямоугольном параллелепипеде АВСDА₁ВСD₁ известны ребра АВ=6, АD=4, АА₁=10. Точка F принадлежит ребру ВВ₁ и делит его в отношении 2:3, считая от вершины В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С₁.

Стандартная ошибка учащихся В прямоугольном параллелепипеде АВСDА₁ВСD₁ известны ребра АВ=6, АВ=4, АА₁=10. Точка F принадлежит ребру ВВ₁ и делит его в отношении 2:3, считая от вершины В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С₁.

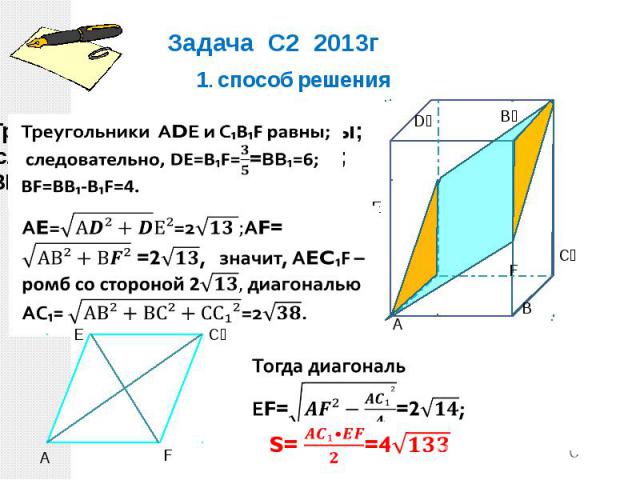
Задача С2 2013г В прямоугольном параллелепипеде АВСDА₁ВСD₁ известны ребра АВ=6, АD=4, АА₁=10. Точка F принадлежит ребру ВВ₁ и делит его в отношении 2:3, считая от вершины В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С₁. Отрезок АЕ параллелен С₁F принадлежит ребруDD₁). Плоскость сечения пересекает плоскостьСС₁D₁ по прямой С₁Е, параллельной АF, Следовательно, искомое сечение -
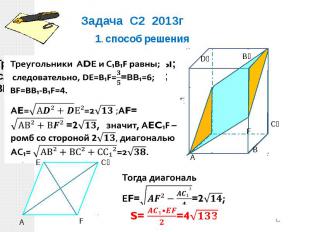
Треугольники АDЕ и С₁В₁F равны; следовательно, DЕ=В₁F=

Задача С2 2013г 1. cпособ решения АE=√(А
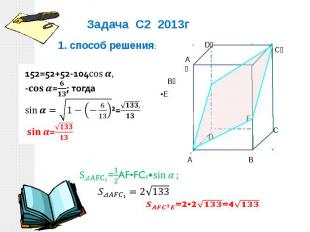
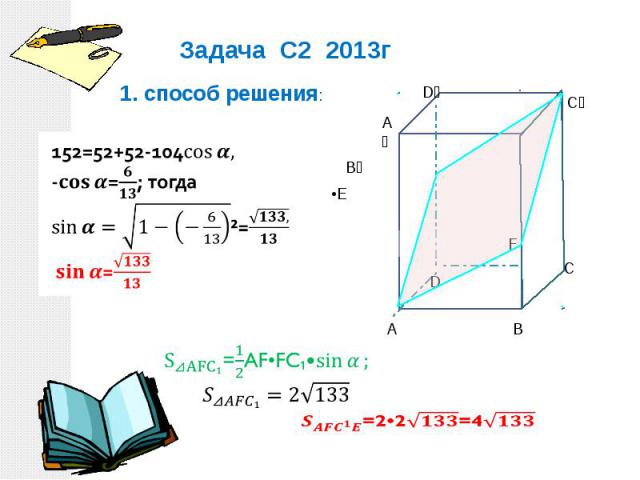
Задача С2 2013г 1. способ решения: 152=52+52-104cos〖
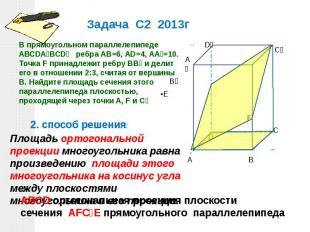
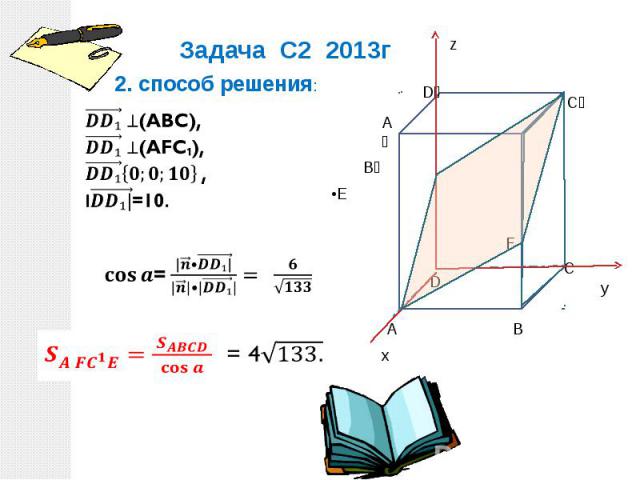
В прямоугольном параллелепипеде АВСDА₁ВСD₁ ребра АВ=6, АD=4, АА₁=10. Точка F принадлежит ребру ВВ₁ и делит его в отношении 2:3, считая от вершины В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С₁ Площадь ортогональной проекции многоугольника равна произведению площади этого многоугольника на косинус угла между плоскостями многоугольника и его проекции. АВСD ортогональная проекция плоскости cечения АFC₁E прямоугольного параллелепипеда
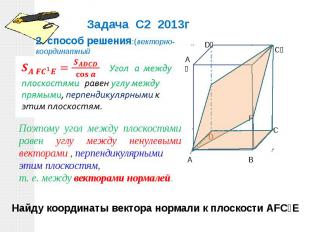
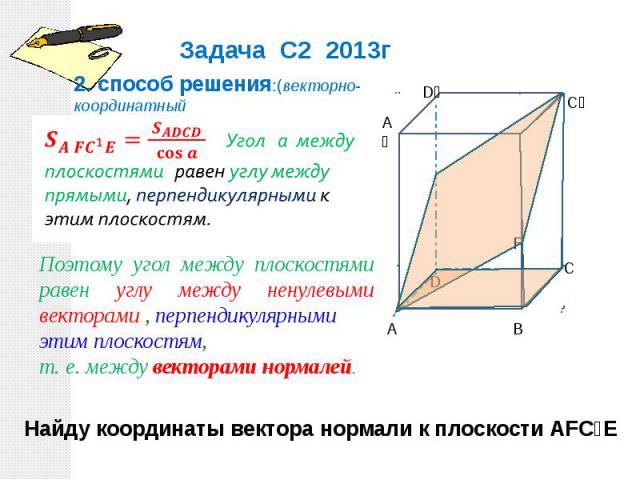
2. cпособ решения:(векторно-координатный метод) Поэтому угол между плоскостями равен углу между ненулевыми векторами , перпендикулярными этим плоскостям, т. е. между векторами нормалей. Найду координаты вектора нормали к плоскости АFC₁E
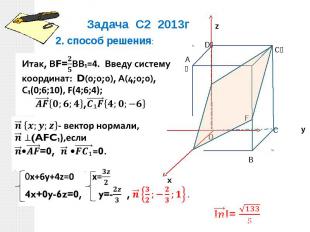
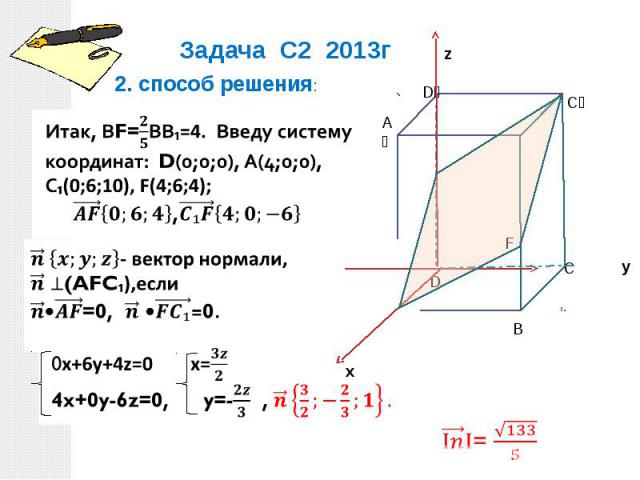
Задача С2 2013г 2. способ решения:Итак, ВF=
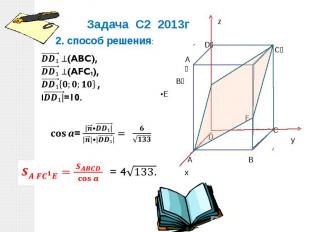
Задача С2 2013г 2. способ решения: (

Литература. Атанасян Л.С. Геометрия: учебник для 10-11 классов общеоразовательных учреждений.-М.: Просвещение,2011.2. Смирнова И.М.,Смирнов В.А. Эффектиная подготовка к ЕГЭ. - М.: Экзамен, 20083. Рыбкин Н. Сборник задач по геометрии. Стереометрия для 9 и 10 классов.-М.: Просвещение, 1972.4.Ким по математике 11класс 2013.