Презентация на тему: Симметрия вокруг нас

Урок-презентация проекта «Симметрия вокруг нас» Над проектом работали учащиеся 9-го класса Руководитель проекта: учитель математики Борюшова Е.А.

«Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всем в жизни симметрия?» Лев Николаевич Толстой

Цели урока: Выявить значение принципа симметрии в алгебре. Выявить архитектурные стили, представленные в Коломне. Научиться определять виды симметрии в природе. Познакомиться с понятиями «асимметрия», «диссимметрия», «антисимметрия». Ответить на вопросы: 1)Во всем ли в жизни симметрия? 2)Только ли симметрия является признаком красоты?

План урока Теоретический блиц-опрос Защита учебных проектов Подведение итогов работы над проектами Домашнее задание

Симметрия…является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство. Г. Вейль

Блиц-опрос Что понимается под движением? 2. Приведите примеры движений.

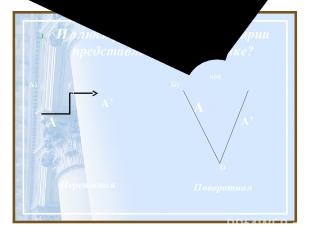
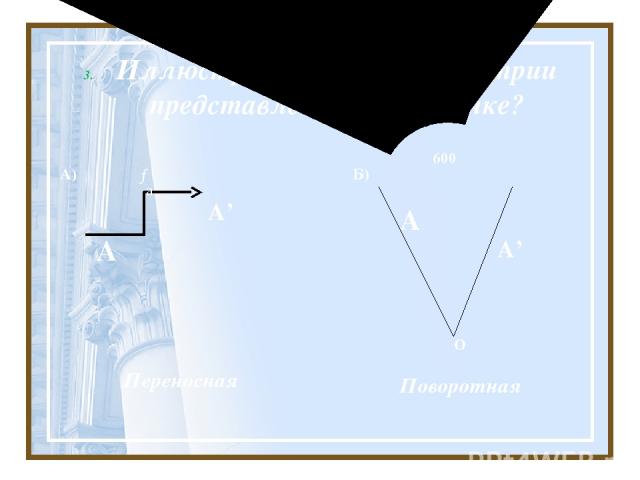
Иллюстрация какой симметрии представлена на рисунке? А) А’ А Переносная → а Б) А А’ 600 Поворотная О

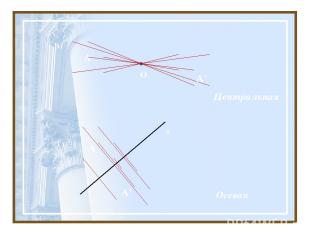
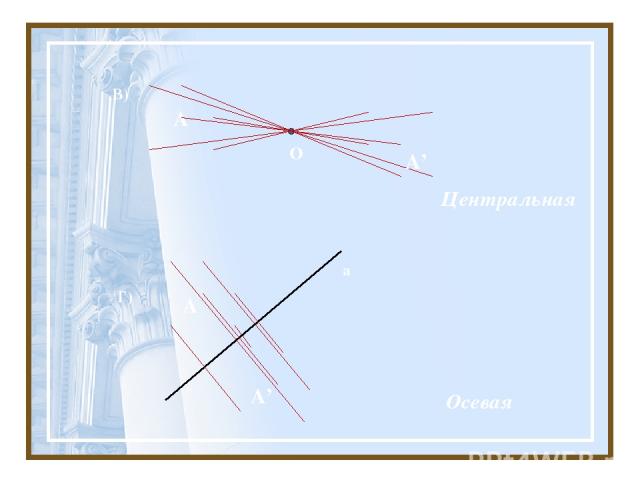
В) А О Центральная Г) a Осевая A’ A A’

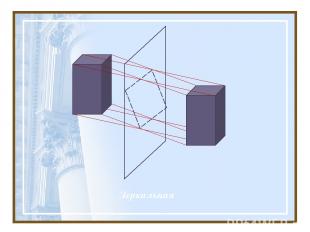
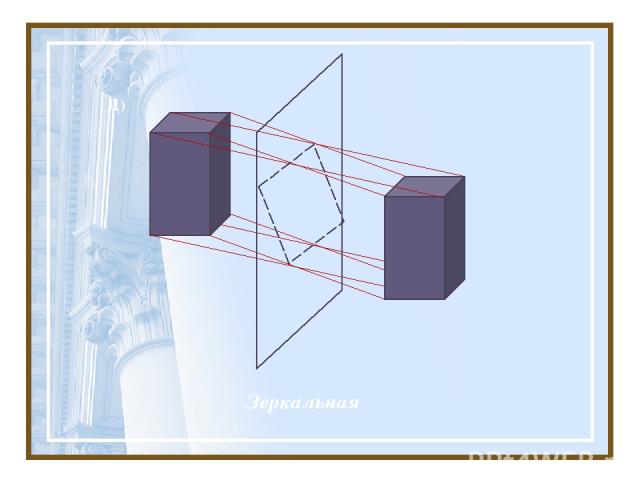
Д) Зеркальная

Защита проектов

Проект 1 группы: «Симметрия в алгебре». Проект подготовили: Гвоздева А. Каплун В. Ковальчук О. Онуфриенко А. Пономаренко К. Ковалева У. Маликов И. Курбанова А.

Симметрия в алгебре

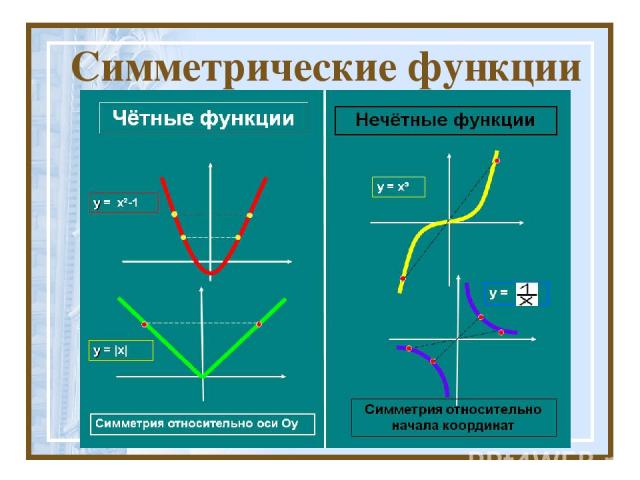
Функция называется чётной, если справедливо равенство                                                                        График чётной функции симметричен относительно оси ординат .         . Функция называется нечётной, если справедливо равенство                                                                              График нечётной функции симметричен относительно начала координат    Пример 1. Доказать, что у = х4 — четная функция. Решение. Имеем: f(х) = х4, f(-х) = (-х)4. Но (-х)4 = х4. Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной. Пример 2. Доказать, что у = х3~ нечетная функция. Решение. Имеем: f(х) = х3, f(-х) = (-х)3. Но (-х)3 = -х3. Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.

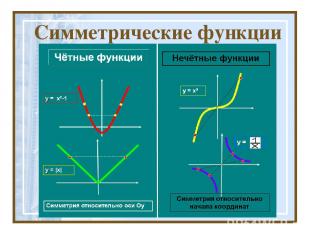
Симметрические функции

Возвратные уравнения 3-й и 4-й степени Многочлены n-ой степени f (x) = anxn + an-1xn-1 + … + a0 называется возвратным, если его коэффициенты, одинаково отдаленные от начала и от конца, равны между собой. Алгебраическое уравнение вида f (x) = 0, где f (x) – возвратный многочлен , называют возвратным уравнением.

2x3+7x 2 +7x+2 = 0 2x3 +2+7x2 +7x = 0 2 (x3 +1) +7x (x+1) = 0 2 (x+1) (x2 –x+1) + 7x (x+1)=0 (x+1) (2x2 - 2x+2+7x)=0 (x+1) (2x2 +5x+2)=0 x+1=0 или 2x 2 +5x +2 =0 x= -1 D= 25 - 16=9 x₁ = -2 x₂ = - 0,5 Ответ:-1;-2;-0,5.

6х4-35х3+62х2-35х+6х2=0 6х2-35х+62-35/х+6=0 6х2+6/х2-35х-35/х+62=0 6(х2+1/х2)-35(х+1/х)+62=0 Х+1/х=z (х+1/х)2=z2 Х2+2+1/х2=z2 Х2+1/х2=z2-2 6(z2-2)-35z+62=0 6z2-12-35z+62=0 6z2-35z+50=0 Д=b2-4ac=(-35)2-4*6*50= 1225-1200= 25 Z1=5/2 Z2= 10/3 х+ 1/х=5/2 х+1/х= 10/3 х+ 1/х-5/2 =0 х+1/х-10/3=0 2х2-5х+2=0 х 0 3х2-10х+3=0 Д=25-4*2*2=9 Д= 100-4*3*3=64 Х1= ½ х2 = 2 Х3= 1/3 Х4 = 3 Ответ:1/2;2;1/3;3.

Системы уравнений второй степени. Система уравнений второй степени – это система уравнений, в которой есть хотя бы одно уравнение второй степени.

Укажите симметричные многочлены: X3+4x2y+4xy2+y3 3x4-8x3y+3y4 X5+Y5 2x4+7x3y+7xy3+2y4

Литература 1. Виленкин Н.Я.Алгебра :издательство «Просвещение» Москва, 1968. 2. Интернет – ресурсы: http://ru.wikipedia.org/wiki/ http://festival.1september.ru/ 3 Болтянский В.Г. и др. Симметрия в алгебре. - М.: Наука, 1967. 4 Башмаков М.И. Уравнения и неравенства. - М.: Наука, 1971. 5 Березин В.Н. и др. Сборник задач для факультативных и внеклассных занятий по математике. Книга для учителя. - М.: Просвещение, 1985. 6 Вавилов В.В. и др. Задачи по математике. Алгебра. - М.: Наука, 1987. 7 Черкасов О.Ю. и др. Математика: Справочник для старшеклассников и поступающих в вузы. - М.: АСТ-Пресс, 2001. 8В.Г.Болтянский, Н.Я.Виленкин Симметрия в алгебре. 2-е издание 9 Винберг Э. Б. Симметрия многочленов. - М.: МЦНМО, 2001. — 24 с: ил. (Серия: «Библиотека „Математическое просвещение"»).

Проект 2 группы: Симметрия в архитектуре «Вдоль Кремлевской стены». Проект подготовили: Тихонова В. Вялых И. Гурина В. Швец С. Короткова В. Вельчев Н.

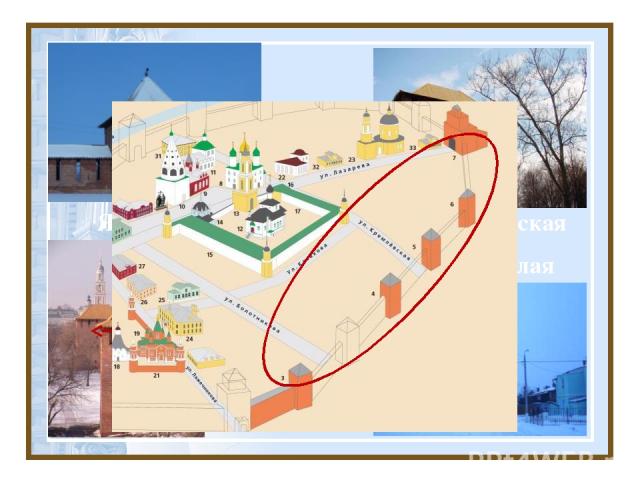
Вдоль Кремлевской стены

« Чувство симметрии и реальное стремление его выразить в быту и в жизни существовало в человечестве с палеолита… Этот опыт многих тысяч поколений ясно указывает на глубокую эмпирическую основу этого понятия…» Академик В.И.Вернадский (1863 – 1945 гг)

«Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии… применение симметрии в первобытном производстве определялось не столько эстетическими мотивами, но в известной мере и уверенностью человека в большей пригодности для практики правильных форм.» Академик А. В. Шубников (1887 – 1970 гг)

Архитектурные стили готика барокко хай-тек модерн классицизм ампир футуризм конструктивизм эклектика

Маринкина башня

Грановитая башня

Ямская Спасская Погорелая Семеновская

Пятницкие ворота

Литература 1.Большаков М.В. Декор и орнамент в книге: Альбом. - М.: Книга, 1990. 2. Волошинов А. В. Математика и искусство. - М.: Просвещение, 2000. 3. Гильде В. Зеркальный мир. — М.: Мир, 1982г. 4. Данилова Г.И. Мировая художественная культура. От истоков до XVII века: учебник для 10 класса общеобразовательных учреждений гуманитарного профиля, 3 изд. - М.: Дрофа, 2006 5. Пилявский В.И., Тиц А.А., Ушаков Ю.С. История Русской архитектуры. Стройиздат, 1984. 6 Интернет-ресурсы: История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков; История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков; История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков; http://festival.1september.ru/ http://www.kolomna-kreml.ru/ http://ru.wikipedia.org/wiki/

Проект 3 группы: «Симметрия в природе» Проект подготовили: Бугаёва Оксана, Пизикс Алёна, Кравченко Катя, Имерели Данил, Пизикс Андрей, Жигалов Саша, Трапезников Коля, Боровиков Саша, Конограев Максим, Гелеверя Вадик.

Симметрия в природе

Симметрия является важнейшим свойством природы. Поразительные по красоте примеры симметрии дают снежинки. Симметрия в природе Снежинка обладает поворотной симметрией.

Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Симметрия у животных радиальная (лучистая) билатеральная

В XX веке усилиями российских учёных - В Беклемишева, В Вернадского, В Алпатова, Г.Гаузе - было создано новое направление в учении о симметрии - биосимметрика На примере дерева просматривается симметрия конуса Симметрия в биологии

У цветковых растений в большинстве проявляется радиальная и билатеральная симметрия. Цветок считается симметричным, когда каждый околоцветник состоит из равного числа частей. Симметрия в биологии

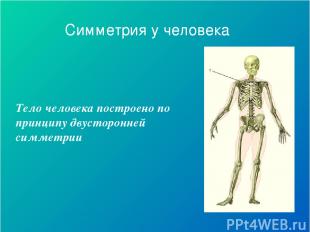
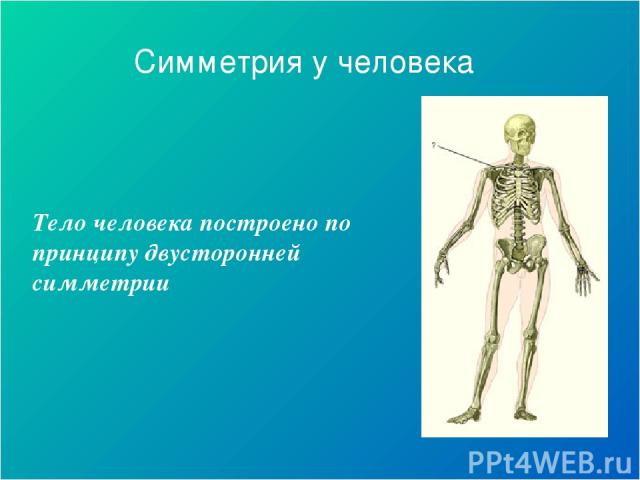
Симметрия у человека Тело человека построено по принципу двусторонней симметрии

Диссимметрия — это частично расстроенная симметрия, противоречивое единство симметрии и асимметрии, обозначающее некоторый упорядоченный отход от симметрии; это асимметрия внутри симметрии и наоборот.

Антисимметрия – это сохранение одного свойства объекта и замена другого свойства на противоположное.

Асимметрия– это отсутствие симметрии.

Асимметрия– это отсутствие симметрии.

Литература Гильде В. Зеркальный мир. — М.: Мир, 1982г Интернет-ресурсы: История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков; История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков; История Русской архитектуры. Стройиздат. 1984 г. В.И.Пилявский, А.А.Тиц, Ю.С.Ушаков; http://festival.1september.ru/ http://ru.wikipedia.org/wiki/

Подведение итога На вопрос «Чему удалось научиться в ходе работы над проектом?» Школьники отвечают:

Домашнее задание На блоге http://borushova1972.blogspot.com скачать кроссворд и ответ отправить на электронный ящик [email protected]