Презентация на тему: Симметрия вокруг нас

Симметрия вокруг нас Выполнила:Ученица МОУ СОШ №7Папоян Нарине НорайровнаРуководитель:учитель математикиКалачева Наталья Анатольевна

СИММЕТРИЯ ВОКРУГ НАС

Цели работы: Рассмотреть, как симметрия проявляется и используется в окружающем нас мире.Рассмотреть, как симметрия используется в школьном курсе алгебры. Изучить литературу по теме исследования. Выделить целесообразность изучения темы. Выделить основные направления применения симметрии в творчестве человека. Выделить вопросы школьного курса алгебры, в которых используется симметрия. Рассмотреть, как симметрия используется при решении задач.

СИММЕТРИЯ ВОКРУГ НАС I.Симметрия. Общие положения. II. Единая Культура на принципах симметрии. III. Симметрия в школьном курсе алгебры. Приложения

I.Симметрия. Общие положения. «Симметрия» – (в перев. с греч.) совместная мера, соразмерность. Симметрия - в широком или узком смысле, в зависимости от того, как вы определяете значение этого понятия, - является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.Г. Вейль
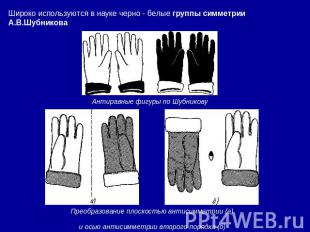
Широко используются в науке черно - белые группы симметрии А.В.Шубникова Антиравные фигуры по Шубникову


Виды симметрии: Симметрия относительно точки (центральная симметрия)

Виды симметрии:Симметрия относительно прямой (осевая симметрия)

Виды симметрии:Скользящая симметрия (переносная симметрия)

Виды симметрии:Симметрия относительно плоскости (зеркальная симметрия)

Глава II. Единая Культура на принципах симметрии. С симметрией в природе мы встречаемся не менее часто, чем в человеческом творчестве. "Параллельность" мира искусства и науки, в первую очередь, проявляется в единстве организации структуры произведения искусства и объекта исследования науки, а это должно сказаться на выборе общего языка для описания структур. Таким языком, на наш взгляд, является язык симметрии. §1. Симметрия в литературе§2. Симметрия в живописи

Симметрия в литературе

Симметрия в литературе

Симметрия в живописи

Симметрия в живописи

Симметрия в живописи

Симметрия вокруг нас

Симметрия вокруг нас

Симметрия вокруг нас Пирамида Чичен Ица Пирамида Чичен Ица (до 800 н.э) Юкатан Пенинсула, Мексика, самый знаменитый храм Майя, служил как политический и экономический центр цивилизации Майя. Целый комплекс различных сооружений - Кукулкан-пирамиды, храм Чак Мол, Зал Тысячи колон и Игровое поле для пленных (их и сегодня можно посетить) – наглядно демонстрирует экстраординарный взгляд на архитектуру и композицию. Пирамида, построенная последней, является самым значительным сооружением среди храмов цивилизации Майя.

Симметрия вокруг нас Дайбуцудэн, или Зал Великого Будды, в монастыре Тодайдзи, - это самое большое деревянное здание в мире, хотя сегодня оно составляет всего лишь две трети от своей первоначальной величины. Множество раз оно горело, и множество раз его восстанавливали. Сегодня оно занимает площадь 58 X 51 метр, а по высоте равно 49 метрам. Зал был построен в VIII веке по приказу императора Шому, и в нем находится одна из самых больших бронзовых статуй мира. В VIII веке буддизм стал государственной религией. Храм Тодайдзи был центром секты Кэгон, которая пришла в Японию через Китай.

Симметрия вокруг нас ЭЙФЕЛЕВА БАШНЯ1889 г., ФранцияДерзновенное сооружение, вершина и торжество технической мысли XIX столетия, прославившееся во всем мире как эмблема Парижа В горизонтальной проекции Эйфелева башня опирается на квадрат площадью в 1,6 гектара. Вместе с антенной ее высота составляет 320,75 метра, она весит 8600 тонн, и, как уверяют специалисты, в процессе ее постройки было заклепано 2,5 миллиона заклепок. 12 000 деталей для башни изготовлялись по точнейшим чертежам. Самая высокая по тем временам башня в мире была смонтирована 250 рабочими в поразительно короткий срок.

Симметрия вокруг нас

Функции и их графики Симметрия используется при работе с понятиями:Четная или нечетная функция. Обратная функция.
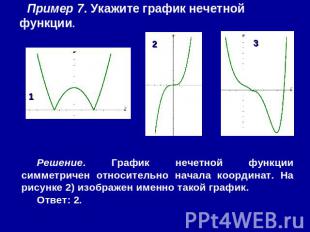
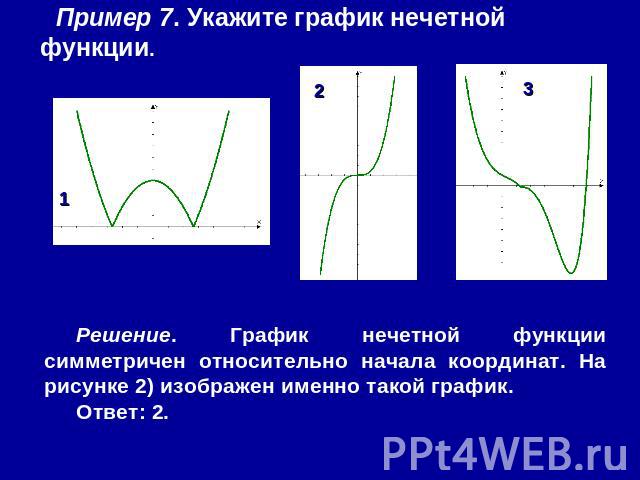
Пример 7. Укажите график нечетной функции. Решение. График нечетной функции симметричен относительно начала координат. На рисунке 2) изображен именно такой график.Ответ: 2.

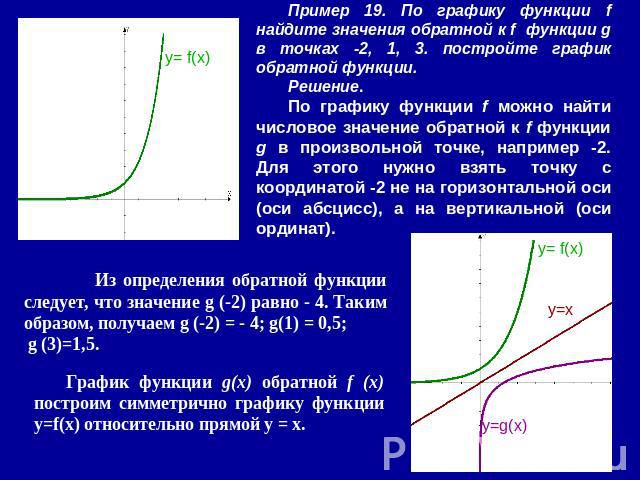
Пример 19. По графику функции f найдите значения обратной к f функции g в точках -2, 1, 3. постройте график обратной функции.Решение. По графику функции f можно найти числовое значение обратной к f функции g в произвольной точке, например -2. Для этого нужно взять точку с координатой -2 не на горизонтальной оси (оси абсцисс), а на вертикальной (оси ординат). Из определения обратной функции следует, что значение g (-2) равно - 4. Таким образом, получаем g (-2) = - 4; g(1) = 0,5; g (3)=1,5. График функции g(х) обратной f (х) построим симметрично графику функции у=f(x) относительно прямой у = х.

Палиндроматика А РОЗА УПАЛА НА ЛАПУ АЗОРА. 42+35=53+24 41-32=23-14 63·48=84·36 82 _ 28 41 ¯ 14

СИММЕТРИЯ ВОКРУГ НАС

СИММЕТРИЯ ВОКРУГ НАС

СИММЕТРИЯ ВОКРУГ НАС

СИММЕТРИЯ ВОКРУГ НАС

СИММЕТРИЯ ВОКРУГ НАС

СИММЕТРИЯ ВОКРУГ НАС