Презентация на тему: Произведение функций

Произведение функций

1. Определение 2. Алгоритм построения 3. Пример №1 4. Пример №2 5. Выполнить построение

Произведением двух функций f(x) и g(x) называется функция h(x) с областью определения, являющейся общей частью областей определения f(x) и g(x), при этом значения функции h(x) = f(x) . g(x).

Алгоритм построения 1) Построить график функций y=f(x)2) Построить график функции y=g(x) в той же системе координат. 3) В каждой точке перемножить длины отрезков, изображающие ординаты графиков, и построить отрезок полученной длины с учетом знака произведения. Множество точек с полученными ординатами представляют график функции h(x)=f(x) . g(x)

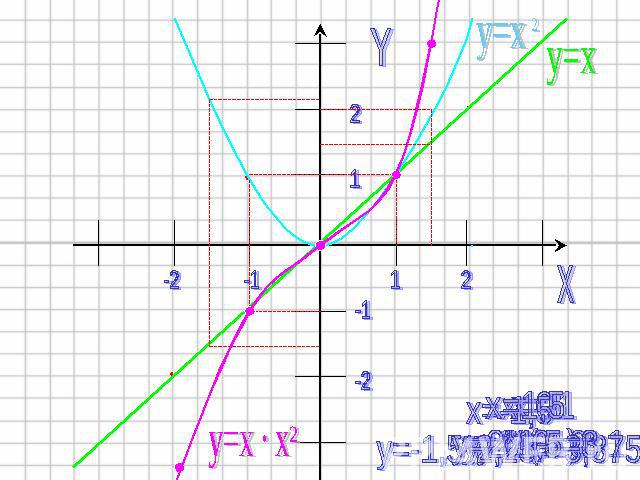
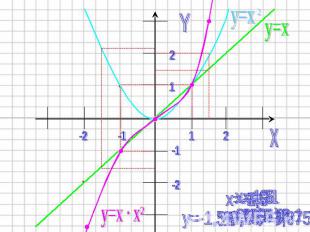
Пример №1Построить функцию y=x.x2

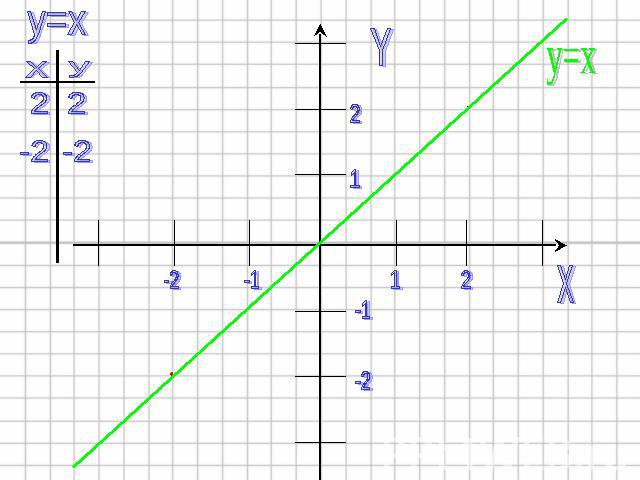
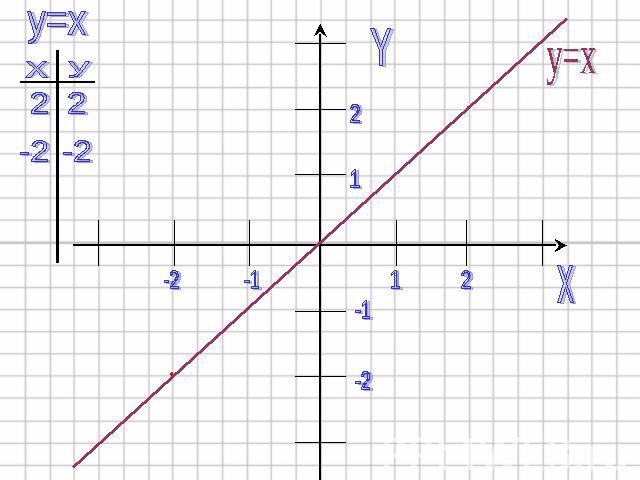
1) Строим график функции y=x Графиком этой функции является прямая. Биссектриса I и III координатных углов.

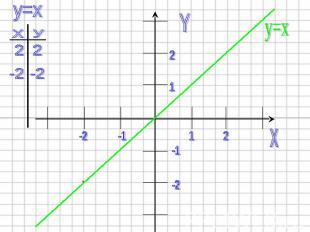
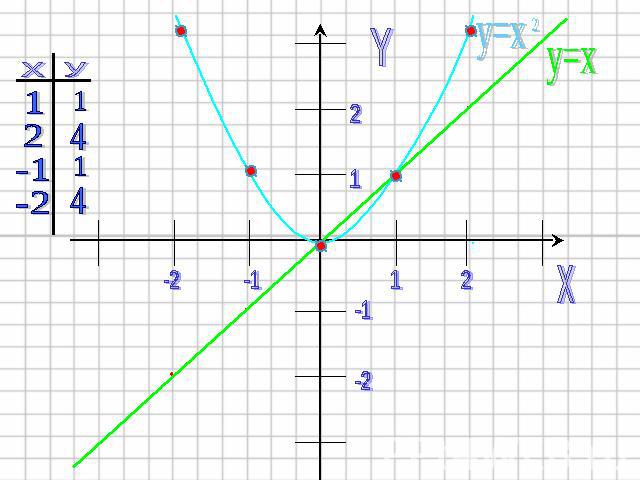
2) Строим график функции y=x2 в той же системе координат. Графиком этой функции является парабола Ветви направлены вверх (т.к. a=1>0) Вершина находится в точке O(0;0).

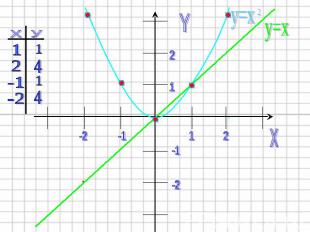
3) В каждой точке перемножить длины отрезков, изображающие ординаты графиков, и построить отрезок полученной длины с учетом знака произведения.

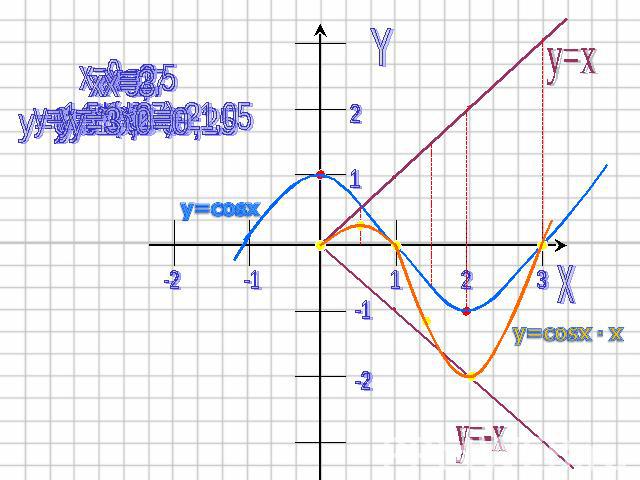
Пример №2Построить функцию y=x . cosx

Функция y=x .cosx является нечетной (она представляет собой произведение четной и нечетной функций), поэтому ее график будет симметричным относительно начала координат и его достаточно построить лишь для х>0.

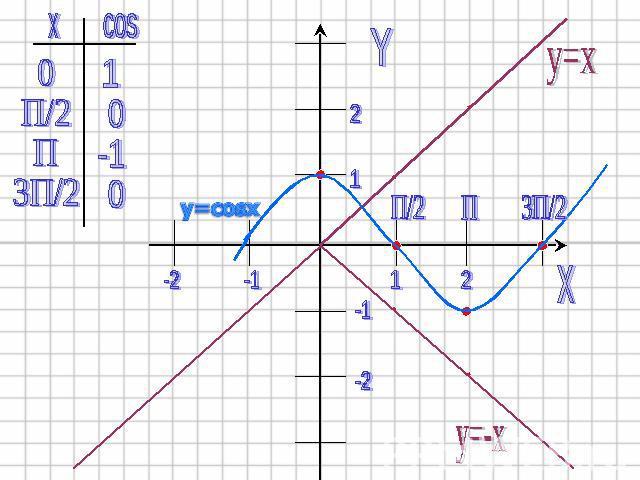
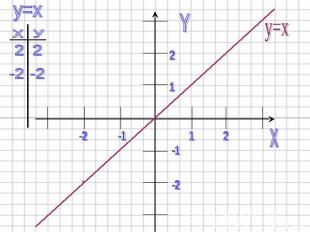
1)Строим график функции y=x. Графиком этой функции является прямая. Биссектриса I и III координатных углов.

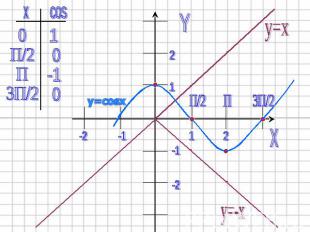
2)Построим график функции y=cosx. Заметим, что в точках x=П/2+Пk, в которых cosx=0, функция равна нулю. В точках x=2Пk, где cosx=1, произведение равно 2Пk, т.е. эти точки лежат на прямой y=x, а в точках x=П+Пk, где cosx=-1, произведение равно –(П+2Пk), т.е. эти точки лежат на прямой y=-x.

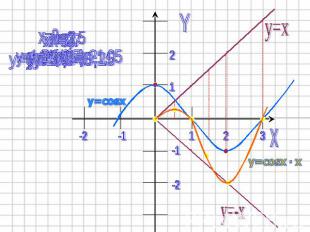
3) В каждой точке перемножить длины отрезков, изображающие ординаты графиков, и построить отрезок полученной длины с учетом знака произведения.

Постройте графики функций y=x .(x-4)2y=1/x . xy=x . x3