Презентация на тему: Применение симметрии при решении алгебраических задач

Применение симметрии при решении алгебраических задач Учениц 10И класса:Коротковой АнастасииЖуравлёвой ДарьиРуководитель:учитель высшей категорииТимофеева М. Н. 

Цель работы: глубже изучить понятие «симметрия» и ее практическое применение. Задачи:• изучить виды симметрии, преобразования;• изучить понятие «функция», способы задания функции, свойства функции;• изучить методы решения уравнений высших степеней;• показать практическое применение данных вопросов.

Существуют преобразования, которые сохраняют расстояния между точками (движение) и преобразования, которые изменяют расстояния между точками в некоторое число раз (гомотетия – подобие ). Симметрия – движение, преобразование плоскости или пространства, при котором сохраняется расстояние между точками. Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х из множества Х соответствует единственное значение переменной у из множества Y. Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.

Чётность функции.Функция у=f(х) может быть чётной или нечётной, если её область определения симметрична относительно 0;Чётная функция: f(х)=f(-х) для любых х из D(у);Нечётная функция: -f(х)=f(-х) для любых х из D(у);Если не выполняется ни одно из соотношений, то функцию называют ни чётной, ни нечётной. Монотонность функции.Функция у=f(х) монотонно возрастает на промежутке I, если для любых х1 и х2 из I таких, что х1<х2, выполняется неравенство f(х1)<f(х2);Функция у=f(х) монотонно убывает на промежутке I, если для любых х1 и х2 из I таких, что х1<х2, выполняется неравенство f(х1)>f(х2).

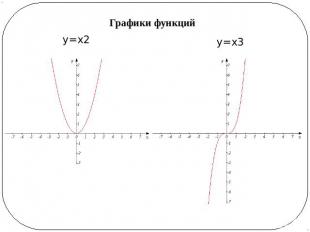
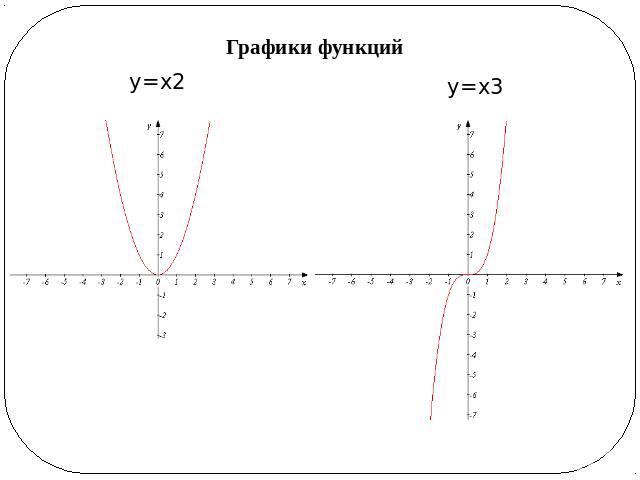
Графики функций у=х2 у=х3

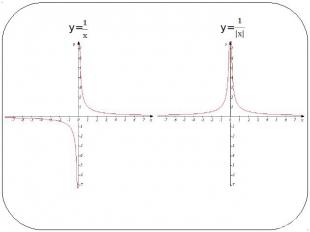
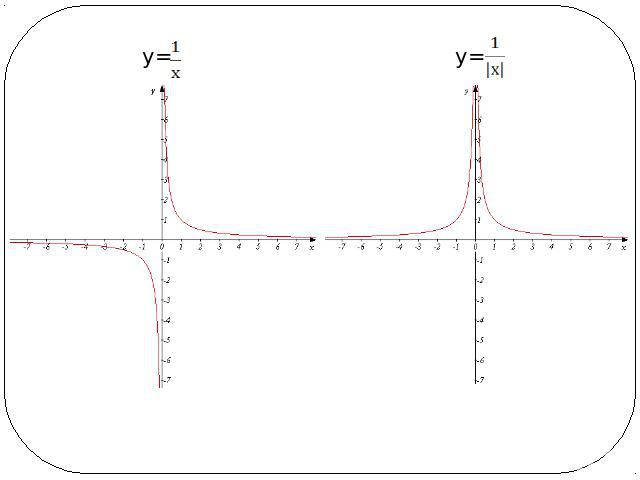
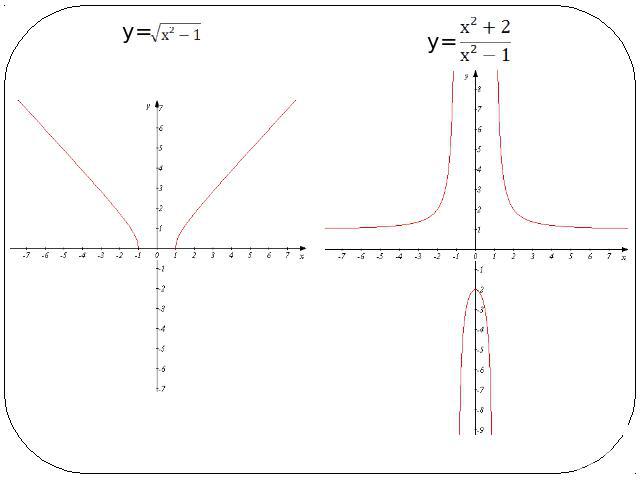
у=

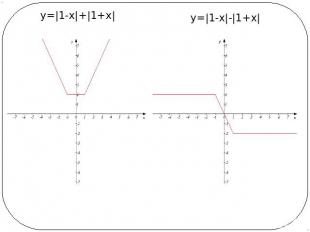
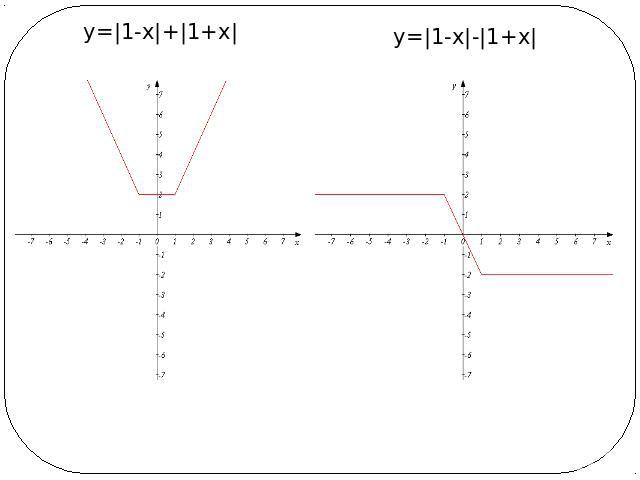
у=|1-х|+|1+х| у=|1-х|-|1+х|

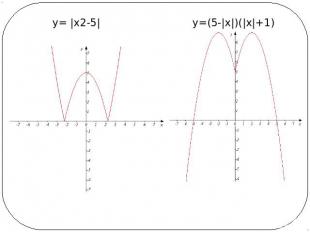
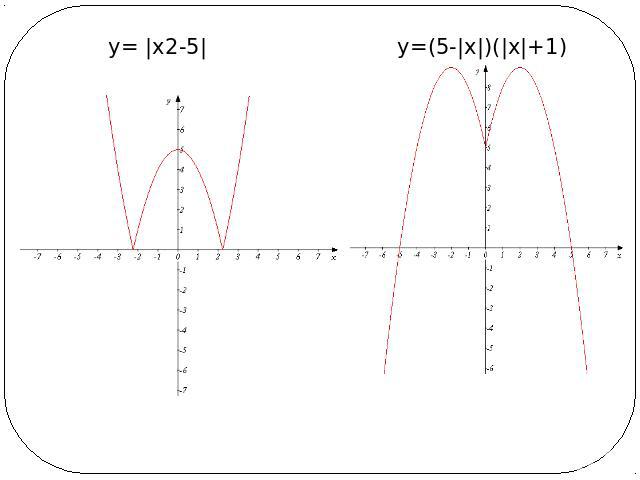
у= |х2-5| у=(5-|х|)(|х|+1)

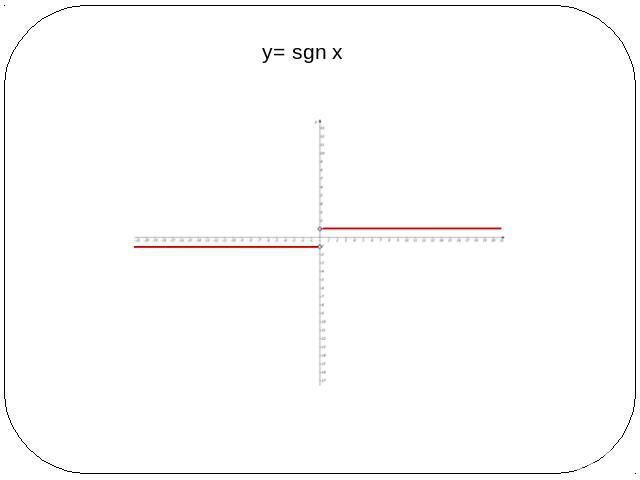
y= sgn x

Решение систем нелинейных уравнений с параметром графически Пример: дана система уравненийНайти количество решений в зависимости от параметра а

Ответ: 0<а< или а>1,то нет решений;если а= или а=1, то решений 4;если <a<1, то решений восемь.

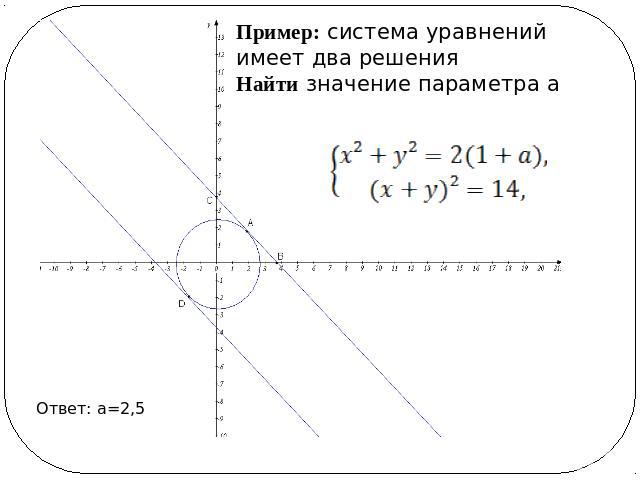
Пример: система уравнений имеет два решенияНайти значение параметра а

Решение некоторых уравнений аналитическими методами, основанных на симметрии Уравнение вида … Где ,…, - некоторые числа , , x- переменная, называется уравнением n- степени от одной переменной x.

Симметрическое(возвратное) уравнение четвёртой степени где а≠0

Решение симметрических уравнений высших степеней x=0 не является корнем уравнения, значит разделим обе части уравнения на Пусть получим Возвращаясь к уравнению замены, получим

Решить уравнение (1-12x)(1-6x)(1-4x)(1-3x)=5 (12x-1)(6x-1)(4x-1)(3x-1)=5 Соответствующие корни исходного уравнения равны

, где ab= cd Решить уравнение.

Уравнение вида можно решить, используя метод симметризации, т.е. делая замену Решить x=y+3 , тогда, пусть , получим

Уравнения с параметром Пример: может ли уравнение иметь три корня (№6.221,математика-11). X=0 не является корнем уравненияОтвет: данное уравнение не может иметь три корня.

Использование свойств четности при решении уравнений Пример (ЕГЭ 2008): дана функция g(x)=2,3+f(x-9)и нечетная функция f(x) , найти значение выражения g(6)+g(8)+g(10)+g(12).Решение: Ответ: g(6)+g(8)+g(10)+g(12)=9,2

Пример(Межрегиональная заочная математическая олимпиада 2008): представьте произвольную функцию f(x), определенную на всей действительной оси, в виде суммы четной и нечетной функций. Решение: y=f(x), D(y)=Rf(x)=g(x)+h(x), где g(x)- четная функция,h(x)- нечетная функцияf(-x)= g(-x)+h(-x), f(-x)= g(x)-h(x), составим систему уравнений

Пример(ЕГЭ 2008): нечетная функция y=f(x) определена на всей числовой прямой. Для всякого неотрицательного значения переменной x значение этой функции совпадает со значением функции g(x)=x(2x+1)(2x-1). Найдите значение функции Решение: Ответ: 1,5 g(-3)=-105, g(3)=105h(-3)=1,5