Презентация на тему: Графы и их применение к решению задач

Выполнила: Артюшевская Елена.г. Елец, Липецкая область, МОУ лицей № 5,8 «Б» класс.

Как известно, умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Поэтому любой экзамен по математике, любая проверка знаний содержит в качестве основной и, пожалуй, наиболее трудной части решение задач.

Решение текстовых задач - это деятельность, сложная для большинства учащихся. Цель данной работы - поиск новых и эффективных, не описанных в учебниках способов решения различных задач, доступных для понимания и применения основной массой школьников.

Рекомендации. Для того, чтобы научиться решать задачи, надо разобраться в том, как они устроены, из каких частей состоят. Каковы инструменты, с помощью которых проводится решение задач.

Чтобы легче решать задачи надо знать следующий алгоритм:1.О каком процессе идет речь в задаче?2.Какие величины характеризуют этот процесс?3.Каким соотношением связаны эти величины?4.Сколько различных процессов описывается в задаче?5.Есть ли связь между элементами? Надо отвечать на эти вопросы, анализировать условие задачи и записывать его схематично.

Решать многие математические задачи помогают специальные схемы, состоящие из точек и соединяющих их дуг или стрелок.Такие схемы называют графами, точки – вершинами графа, а дуги –ребрами графа.

Определения: Граф - это два непустых множества, элементы первого называются вершинами, а второго –ребрами. Каждое ребро соединяет не более двух вершин и любую пару вершин соединяет не более, чем одно ребро.Граф связный, если из любой вершины можно пройти в любую другую по ребрам. Циклом называется замкнутый путь из ребер, а деревом –связный граф без циклов.

С помощью графов можно решать задачи:1) Логические;2) Комбинаторные;3) Алгебраические: на движение, на совместную работу.

Известно, что из 6 гангстеров двое участвовали в ограблении. На вопрос кто участвовал в ограблении, они дали следующие ответы: Дональд: Том и Чарли. Гарри: Чарли и Джордж.Чарли: Дональд и Джеймс. Джеймс: Дональд и Том.Джордж: Гарри и Чарли. Поймать Тома не удалось. Кто участвовал в ограблении, если известно. что четверо гангстеров верно назвали одного из участников ограбления, а один назвал неверно оба имени?

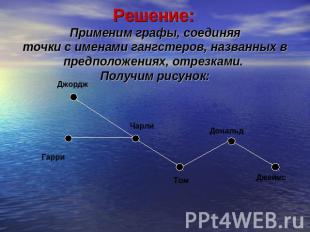
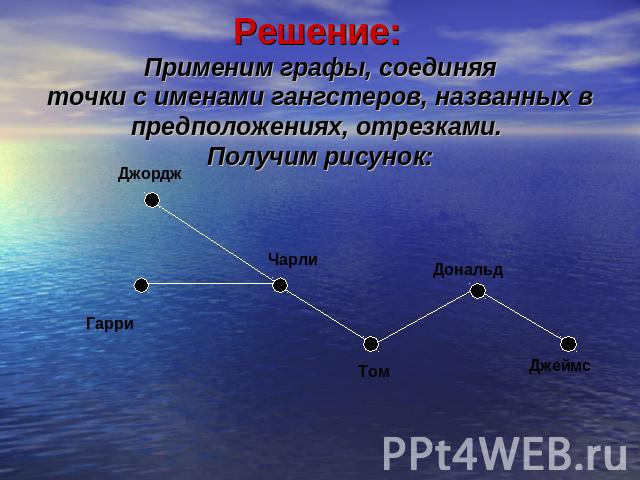
Решение: Применим графы, соединяяточки с именами гангстеров, названных впредположениях, отрезками. Получим рисунок:

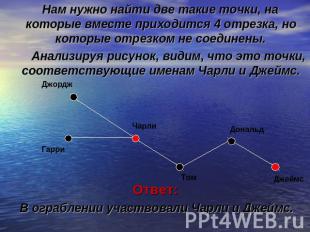
Нам нужно найти две такие точки, на которые вместе приходится 4 отрезка, но которые отрезком не соединены. Анализируя рисунок, видим, что это точки, соответствующие именам Чарли и Джеймс.Ответ: В ограблении участвовали Чарли и Джеймс.

Комбинаторная задача. У каждого из четырёх друзей есть в лесу свой шалаш. Они решили установить между собой связь с помощью проволочного телефона. Вопрос: какое наименьшее количество линий из проволоки им придётся провести, чтобы каждый из них мог поговорить с каждым?

Решение: Ответ: им придется провести не меньше шести линий из проволоки.

Турист проехал на велосипеде 28км по шоссе и 25км по просёлочной дороге, затратив на весь путь 3 часа 30 минут. С какой скоростью ехал турист по проселочной дороге, если известно, что по шоссе он ехал в 1,4 раза быстрее?

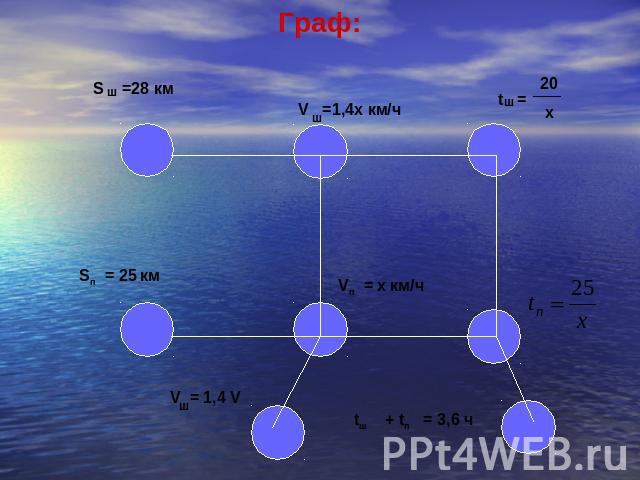
Последовательно отвечая на вопросы слайда 6, анализируем условие задачи и схематично его записываем с помощью графа. Такой граф называется сетевым. Этим способом можно решать текстовые задачи, величины которых связаны соотношением А=ВС, то есть задачи на движение, на совместную работу, заполнение бассейна водой – как раз те, которые вызывают наибольшие трудности у школьников

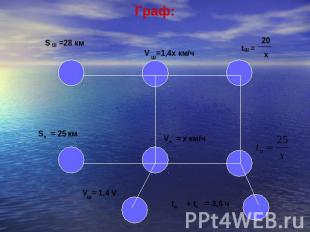
Пусть скорость, с которой турист ехал по просёлочной дороге, равна х км/ч. Тогда, согласно условию задачи скорость, с которой он двигался по шоссе, равна 1,4 х км/ч.Время, затраченное им на движение по шоссе, равно 28:1,4х=20:х ч, а время прохождения просёлочной дороги равно (25:х) ч.По условию задачи их сумма равна 3,6 ч.

Составим уравнение:Значит, турист ехал по просёлочной дороге со скоростью 12,5 км/ч.Ответ: турист ехал по просёлочной дороге со скоростью 12,5 км/ч.

Задача на совместную работу. Два экскаватора, работая одновременно, выполняют некоторый объём земляных работ за 3часа 45 минут. Один экскаватор, работая отдельно, сможет выполнить этот объём работы на 4 ч быстрее, чем другой. Сколько времени требуется каждому экскаватору в отдельности для выполнения того же объёма земляных работ?

Здесь пригодится тот алгоритм, который был в начале работы:1.О каком процессе идёт речь в задаче?- О работе.2.Какие величины характеризуют этот процесс?- Работа, производительность, время.3.Каким соотношением связаны эти величины?- А=k*t.4.Сколько различных процессов описывается в задаче?- Два: работы двух экскаваторов в отдельности и их совместная работа.5.Есть ли связь между элементами? -Да, это связь между временем выполнения работы первого и второго экскаватора.

Сетевой граф в данном случае будет выглядеть так:

Уравнение к задаче составим по нижнему, «горизонтальному» ребру. Составим уравнение:1х Его корнями будут числа 6 и -2,5, последнее из которых отбрасываем ввиду того , что время- величина положительная.

Значит, время, за которое первый экскаватор выполнит этот объём работы, равно 6 часам, а второй экскаватор выполнит за 10 час Ответ: 6 ч, 10 ч.

Вывод: С помощью графов легче решать сложные задачи.

Литература: Ткачук В. В. Математика – абитуриенту. –М.:МЦ НМО, 1997Кузнецова Л. В. Алгебра: сборник заданий для проведения письменного экзамена по алгебре за курс основной школы.- М.: Дрофа, 2002.