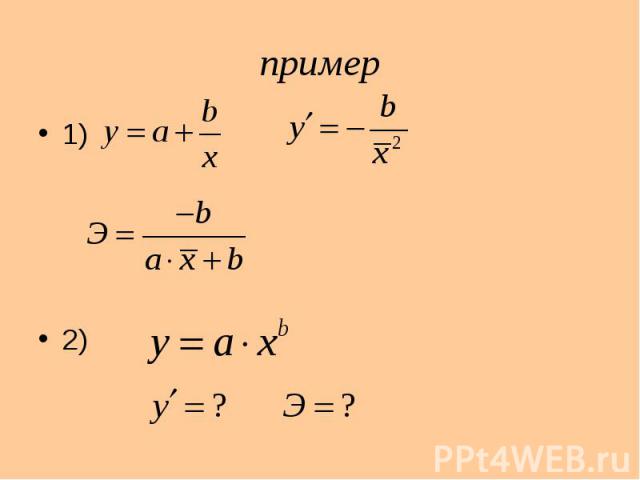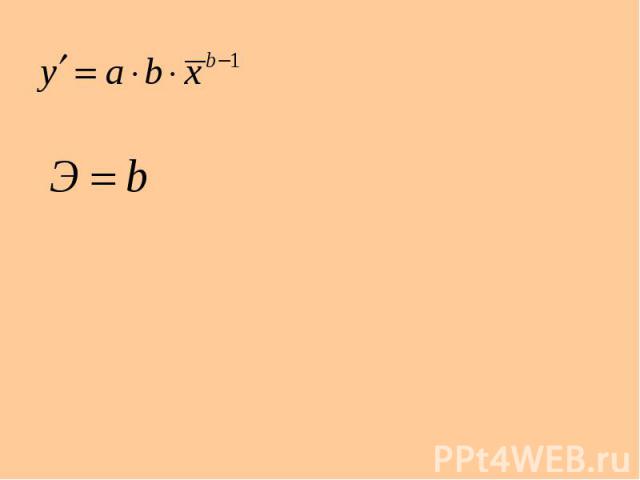Презентация на тему: Коэффициент эластичности

коэффициент эластичности коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:

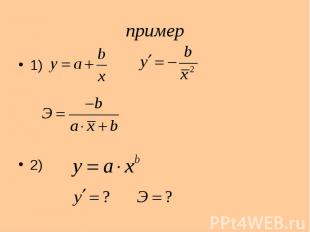
пример 1) 2)

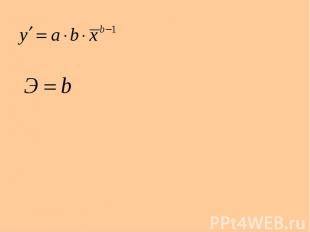
Прогнозное значение определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения .

пример Выполнить, по уравнению регрессии y=280+5,6x, прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x, составляющем 127% от среднего уровня (xp=6700).

средняя стандартная ошибка прогноза :

доверительный интервал прогноза доверительный интервал прогноза

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций

Различают два класса нелинейных регрессий: Различают два класса нелинейных регрессий: 1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам; 2) регрессии, нелинейные по оцениваемым параметрам.

Примером нелинейных регрессий по переменным могут служить следующие функции: Примером нелинейных регрессий по переменным могут служить следующие функции: - полиномы разных степеней - равносторонняя гипербола - .

К нелинейным регрессиям по оцениваемым параметрам относятся функции: - степенная - показательная - экспоненциальная

Нелинейная регрессия определяется, как в линейной регрессии, методом наименьших квадратов (МНК).

в параболе второй степени , в параболе второй степени , заменяя переменные , получим двухфакторное уравнение линейной регрессии:

для полинома k-го порядка для полинома k-го порядка получим линейную модель множественной регрессии с k объясняющими переменными:

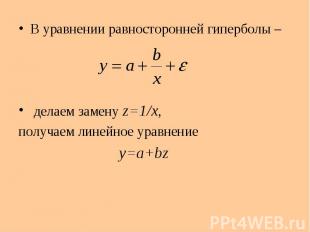
В уравнении равносторонней гиперболы – В уравнении равносторонней гиперболы – делаем замену z=1/x, получаем линейное уравнение y=a+bz

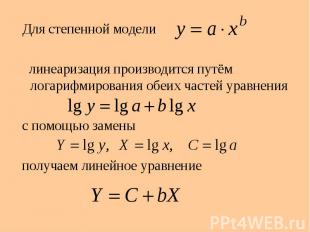
Для степенной модели Для степенной модели линеаризация производится путём логарифмирования обеих частей уравнения с помощью замены получаем линейное уравнение

Для показательной модели Для показательной модели линеаризация производится также с помощью логарифмирования обеих частей уравнения с помощью замены получаем линейное уравнение

Корреляция для нелинейной регрессии. Корреляция для нелинейной регрессии. Величина данного показателя находится в границах: чем ближе к единице, тем теснее связь рассматриваемых признаков.

проверка существенности в целом уравнения нелинейной регрессии осуществляется с помощью F-критерия Фишера проверка существенности в целом уравнения нелинейной регрессии осуществляется с помощью F-критерия Фишера среднее отклонение расчетных значений от фактических для уравнения нелинейной регрессии оценивается с помощью средней ошибки аппроксимации.