Презентация на тему: Коэффициенты квадратной функции

В данном проекте автор специально не использовал теоретическое обоснование, а только выводы на их основе. Для более глубокого и полного изучения этой темы рекомендовано использовать пособия по математике для средней школы. В данном проекте автор специально не использовал теоретическое обоснование, а только выводы на их основе. Для более глубокого и полного изучения этой темы рекомендовано использовать пособия по математике для средней школы.

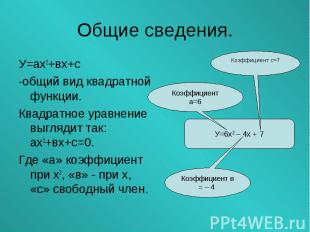
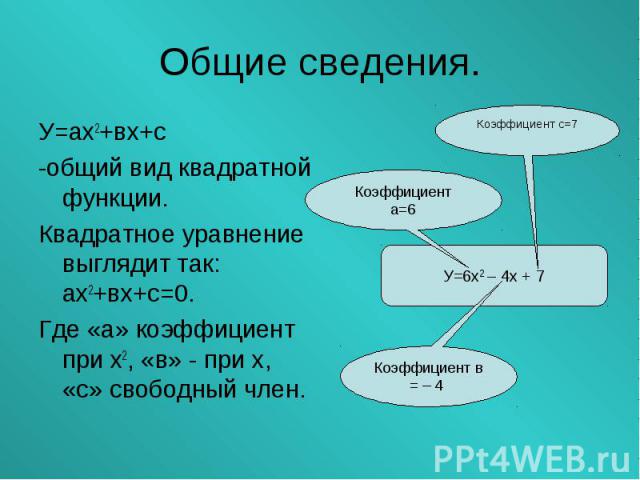
У=ах2+вх+с У=ах2+вх+с -общий вид квадратной функции. Квадратное уравнение выглядит так: ах2+вх+с=0. Где «а» коэффициент при х2, «в» - при х, «с» свободный член.

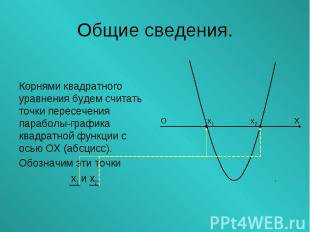
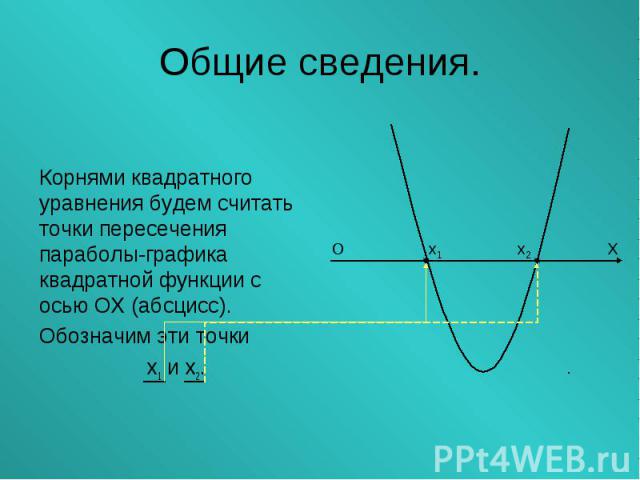
Корнями квадратного уравнения будем считать точки пересечения параболы-графика квадратной функции с осью ОХ (абсцисс). Обозначим эти точки х1 и х2.

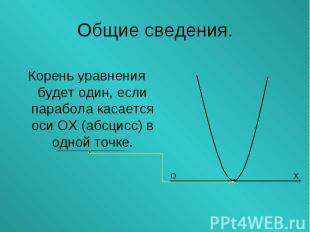
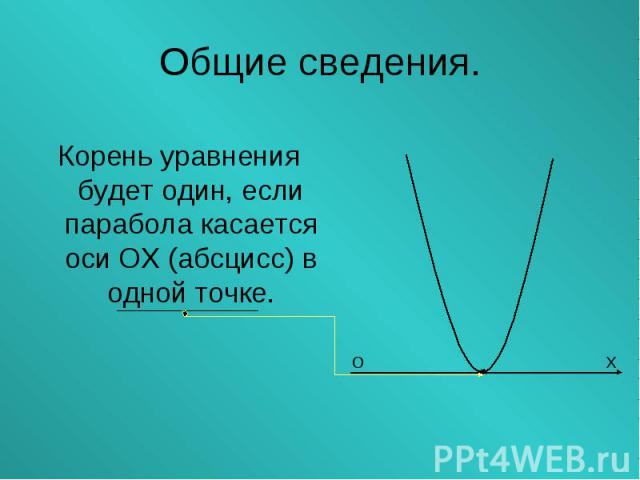
Корень уравнения будет один, если парабола касается оси ОХ (абсцисс) в одной точке. Корень уравнения будет один, если парабола касается оси ОХ (абсцисс) в одной точке.

Коэффициент а – это коэффициент икса в квадрате. От него зависит направление ветвей параболы (вверх или вниз). Коэффициент а – это коэффициент икса в квадрате. От него зависит направление ветвей параболы (вверх или вниз).

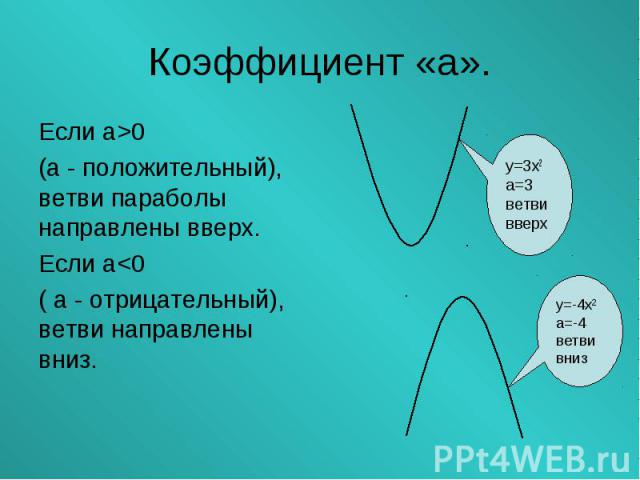
Если а>0 Если а>0 (а - положительный), ветви параболы направлены вверх. Если а<0 ( а - отрицательный), ветви направлены вниз.

Для более удобных рассуждений и работы с коэффициентами «в» и «с» надо обратить внимание на знак коэффициента «а». Для более удобных рассуждений и работы с коэффициентами «в» и «с» надо обратить внимание на знак коэффициента «а». Он должен быть больше ноля. Если «а» отрицательный, то поменяем все знаки в квадратном уравнении умножив его на минус один.

Коэффициент с - это свободный член (число без х). Коэффициент с - это свободный член (число без х). При помощи коэффициента «с» можно сделать вывод о знаках корней уравнения (х1 и х2).

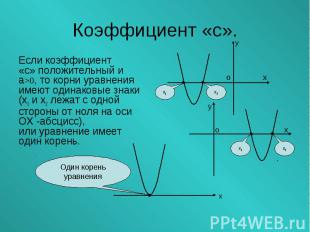
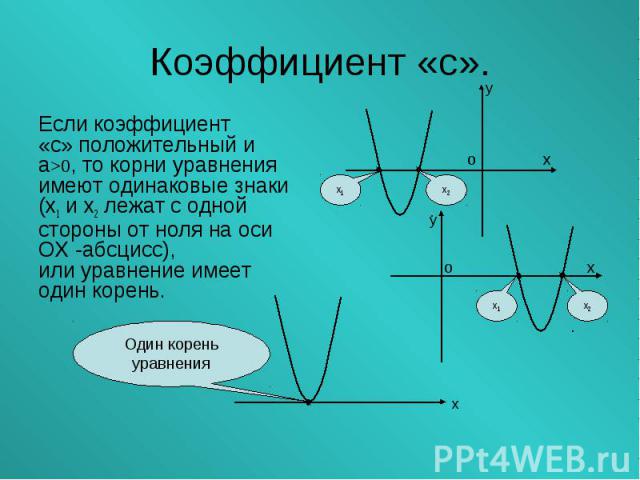
Если коэффициент Если коэффициент «с» положительный и а>0, то корни уравнения имеют одинаковые знаки (х1 и х2 лежат с одной стороны от ноля на оси ОХ -абсцисс), или уравнение имеет один корень.

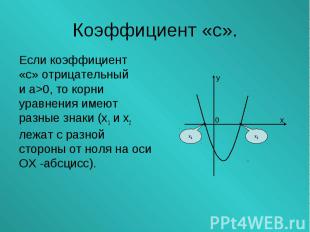
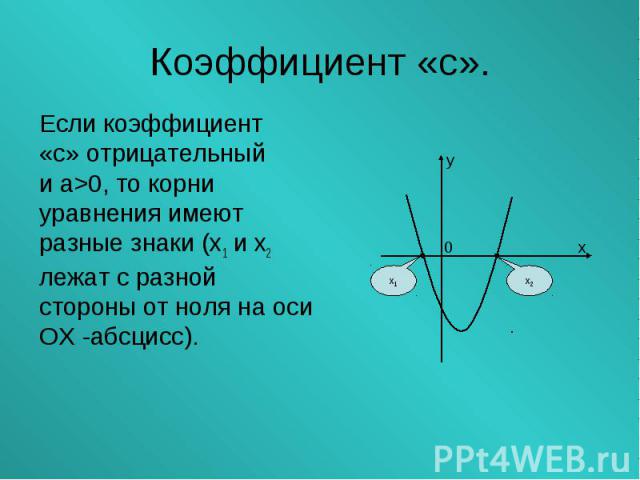
Если коэффициент Если коэффициент «с» отрицательный и а>0, то корни уравнения имеют разные знаки (х1 и х2 лежат с разной стороны от ноля на оси ОХ -абсцисс).

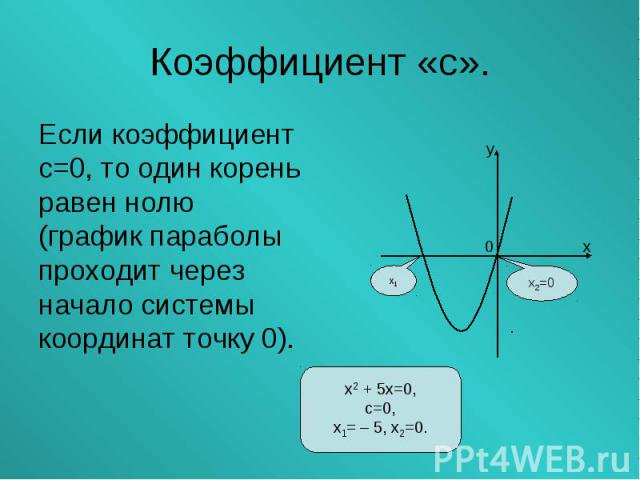
Если коэффициент Если коэффициент с=0, то один корень равен нолю (график параболы проходит через начало системы координат точку 0).

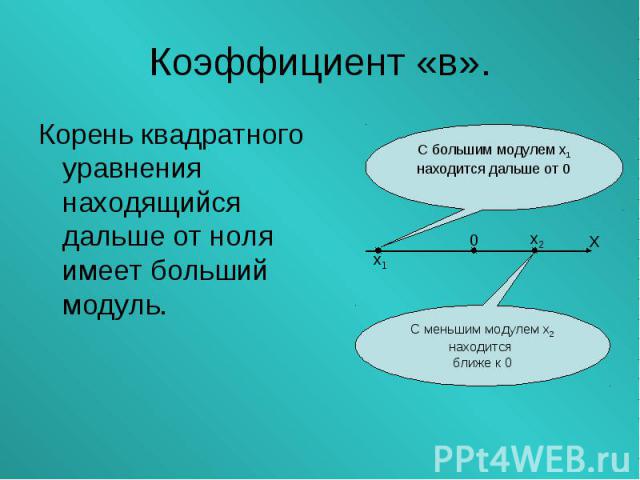
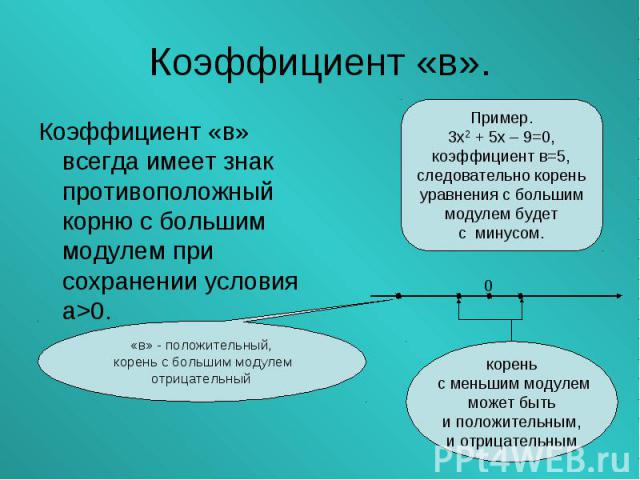
Коэффициент в - это коэффициент икса (число перед х). Коэффициент в - это коэффициент икса (число перед х). При помощи коэффициента «в» можно сделать вывод о знаке корня квадратного уравнения с большим модулем (х1 или х2).

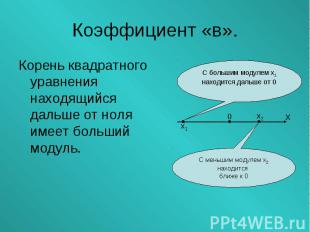
Корень квадратного уравнения находящийся дальше от ноля имеет больший модуль. Корень квадратного уравнения находящийся дальше от ноля имеет больший модуль.

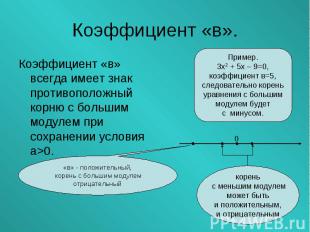
Коэффициент «в» всегда имеет знак противоположный корню с большим модулем при сохранении условия а>0. Коэффициент «в» всегда имеет знак противоположный корню с большим модулем при сохранении условия а>0.

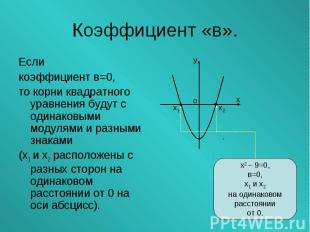
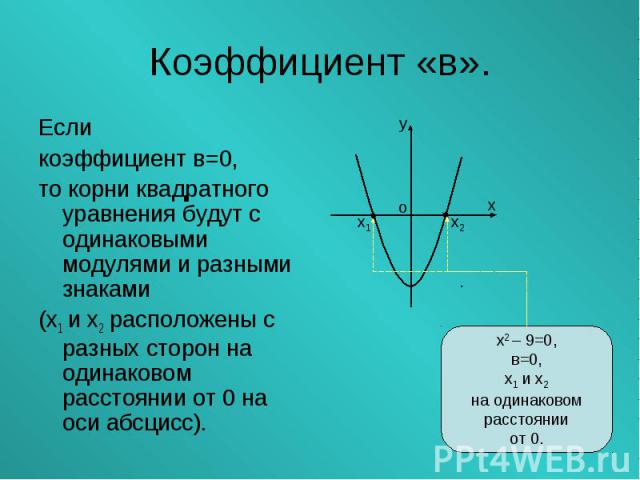
Если Если коэффициент в=0, то корни квадратного уравнения будут с одинаковыми модулями и разными знаками (х1 и х2 расположены с разных сторон на одинаковом расстоянии от 0 на оси абсцисс).

При помощи дискриминанта можно установить количество корней квадратного уравнения или их отсутствие. При помощи дискриминанта можно установить количество корней квадратного уравнения или их отсутствие. Дискриминант вычисляется по формуле D=в2 – 4ас.

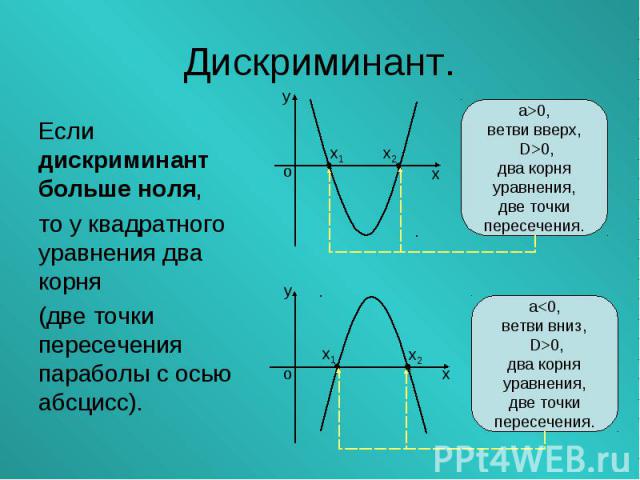
Если дискриминант больше ноля, Если дискриминант больше ноля, то у квадратного уравнения два корня (две точки пересечения параболы с осью абсцисс).

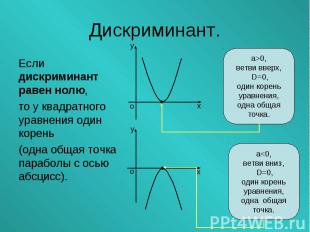
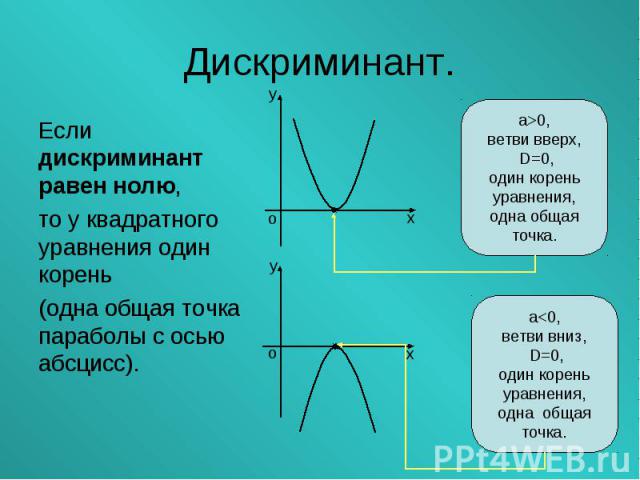
Если дискриминант равен нолю, Если дискриминант равен нолю, то у квадратного уравнения один корень (одна общая точка параболы с осью абсцисс).

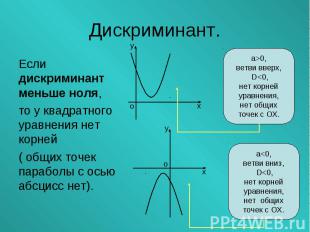
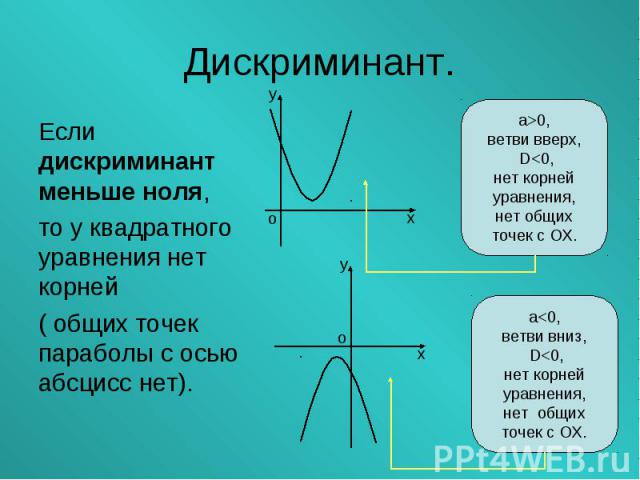
Если дискриминант меньше ноля, Если дискриминант меньше ноля, то у квадратного уравнения нет корней ( общих точек параболы с осью абсцисс нет).

Какое из уравнений соответствует данному рисунку? Какое из уравнений соответствует данному рисунку? а) 5х2 + 2х + 4=0 б) – 2х2 – 6х – 3=0 в) 2х2 + 6х – 4=0 г) 2х2 – 6х + 2=0 д) 2х2 – 6х – 2=0

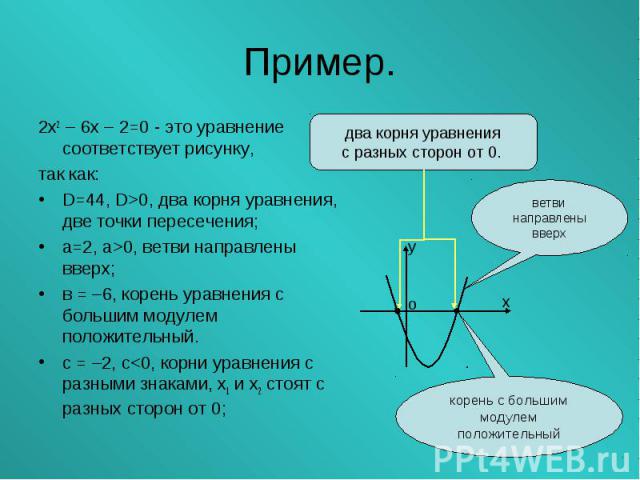
2х2 – 6х – 2=0 - это уравнение соответствует рисунку, 2х2 – 6х – 2=0 - это уравнение соответствует рисунку, так как: D=44, D>0, два корня уравнения, две точки пересечения; а=2, а>0, ветви направлены вверх; в = –6, корень уравнения с большим модулем положительный. с = –2, с<0, корни уравнения с разными знаками, х1 и х2 стоят с разных сторон от 0;

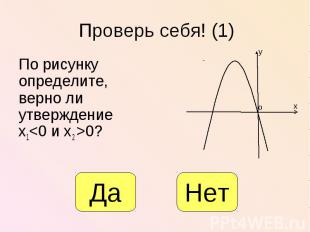
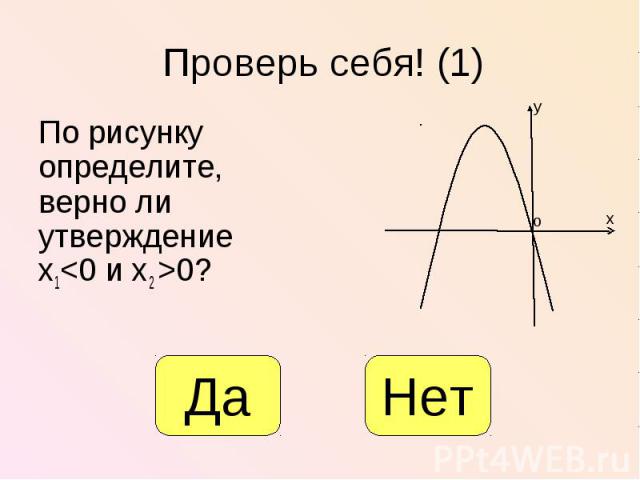
По рисунку определите, верно ли утверждение х1<0 и х2 >0? По рисунку определите, верно ли утверждение х1<0 и х2 >0?

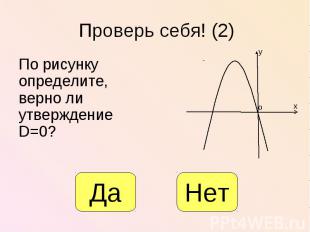
По рисунку определите, верно ли утверждение D=0? По рисунку определите, верно ли утверждение D=0?

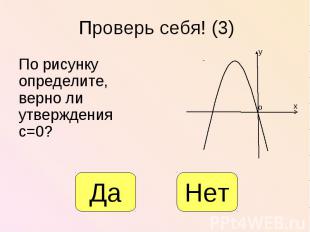
По рисунку определите, верно ли утверждения с=0? По рисунку определите, верно ли утверждения с=0?

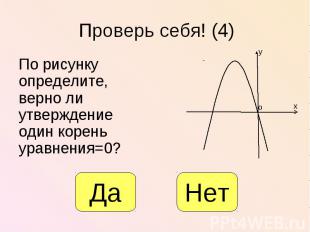
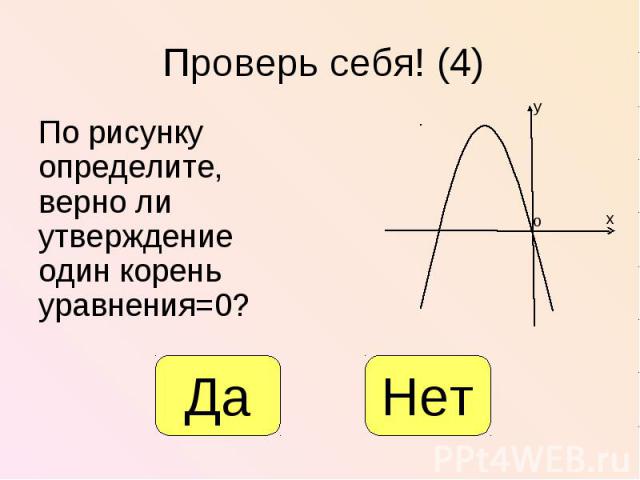
По рисунку определите, верно ли утверждение один корень уравнения=0? По рисунку определите, верно ли утверждение один корень уравнения=0?

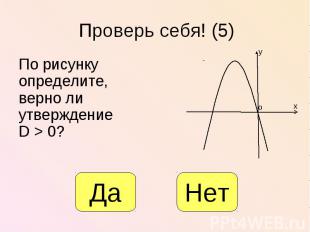
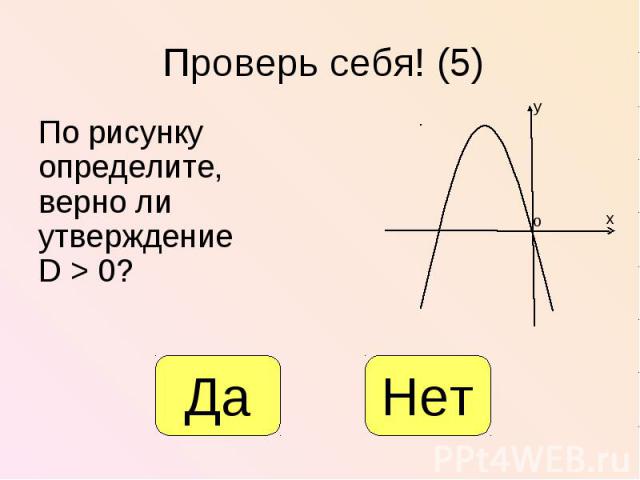
По рисунку определите, верно ли утверждение D > 0? По рисунку определите, верно ли утверждение D > 0?

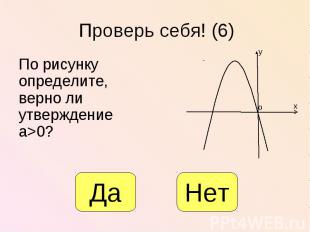
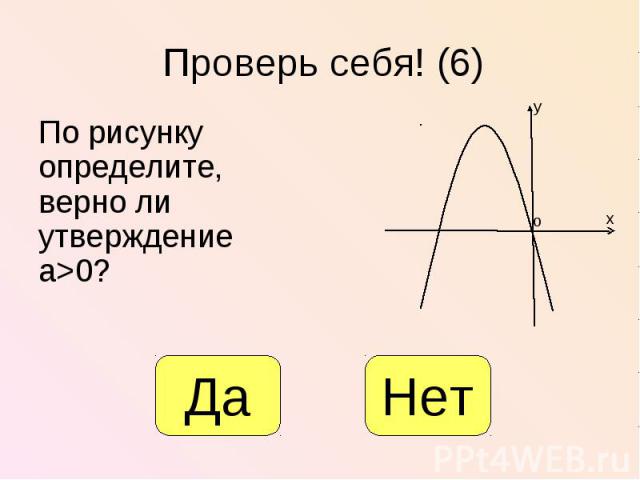
По рисунку определите, верно ли утверждение а>0? По рисунку определите, верно ли утверждение а>0?

Литература: учебники алгебры для средней школы авторских групп А. Г. Мордковича, Г. К. Муравина, Литература: учебники алгебры для средней школы авторских групп А. Г. Мордковича, Г. К. Муравина, Ш. А. Алимова. Экспертиза: учителей 1 категории МОУ Краснодесантской СОШ В. Н. Маличенко, С. В. Шувалов.