Презентация на тему: Формулы сокращённого умножения

Формулы сокращённого умножения Знание - самое превосходное из владений. Все стремятся к нему, само оно не приходит.

Здравствуйте!Мальчики и девочки! Я - ваш помощник, сегодня мы познакомимся с формулами сокращенного умножения, которые позволяют не умножать каждый раз один многочлен на другой, а пользоваться готовым результатом.Мы рассмотрим два способа доказательства формул и примеры их применения, а также вам будут предложены задания для самопроверки. Желаю удачи!

Квадрат суммыКВАДРАТ СУММЫ ДВУХ ВЫРАЖЕНИЙ РАВЕН СУММЕ ИХ КВАДРАТОВ ПЛЮС ИХ УДВОЕННОЕ ПРОИЗВЕДЕНИЕ(a+b)2=(a 2 +2ab + b 2)Доказательство:(a+b)2 = (a+b) (a+b) = a·a + a·b + b·a + b·b = a2+ab+ab+b2= a2 + 2ab +b2

ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО Пусть a и b — положительные числа. Рассмотрим квадрат со стороной a+b и вырежем в двух его углах квадраты со сторонами a и b. Площадь квадрата со стороной a+b равна (a+b)²Этот квадрат мы разрезали на 4 части: квадрат со стороной a (его площадь a²), квадрат со стороной b (его площадь b²), 2 прямоугольника со сторонами a и b (площадь каждого прямоугольника равна ab)Значит, (a + b)² = a² + b² + 2ab

Квадрат разности Квадрат разности двух выражений равен сумме их квадратов минус их удвоенное произведение(a-b)2=(a 2 - 2ab + b 2)Доказательство:(a-b)2 = (a-b) (a-b) = a·a - a·b - b·a + b·b = a2-ab-ab+b2= a2 -2ab +b2

При использовании формул квадрата суммы или квадрата разности учитывайте, что(─a — b)² = (a + b)²;(b — a)² = (a — b)².Это следует из того, что (-а)² = а²

Разность квадратов разность квадратов равна произведению суммы одночленов на их разностьa2-b2=(a+b)(a-b)Доказательство:(a+b)(a-b)= a2-ab+ab-b2= a2-b2
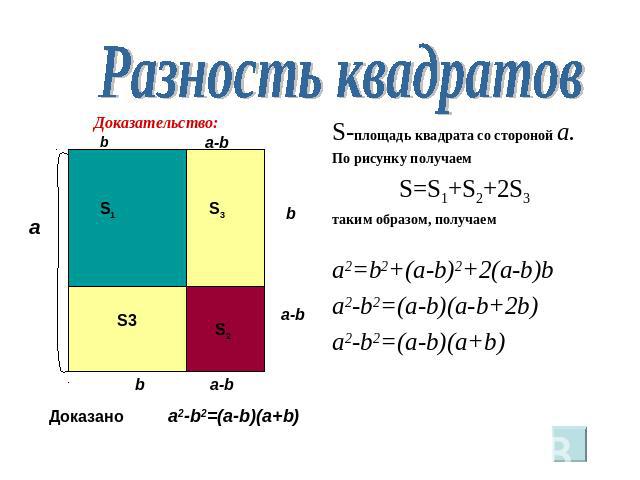
Разность квадратовS-площадь квадрата со стороной a.По рисунку получаем S=S1+S2+2S3таким образом, получаемa2=b2+(a-b)2+2(a-b)ba2-b2=(a-b)(a-b+2b)a2-b2=(a-b)(a+b)

Некоторые математические фокусы Отметим, что на формулах квадрата суммы и квадрата разности основаны некоторые математические фокусы, позволяющие производить вычисления в уме. Например, можно практически устно возводить в квадрат числа, оканчивающиеся на 1, 2, 8 и 9.71² = (70 + 1)² = 70² + 2·70·1 + 1² = 4900 + 140 + 1 = 5041Но самый элегантный фокус связан с возведением в квадрат чисел, оканчивающихся цифрой 5:85² = (80 + 5)² = 80² + 2·80·5 + 5² = 80·(80 + 10) + 25 = = 80·90 + 25 = 7200 + 25 = 7225

Мы рассмотрели два вида доказательства формул сокращенного умножения. Вы увидели, что формулы можно доказать и геометрически.Перейдём к практической работе.Сейчас я вам покажу как применяются эти формулы при решении задач. Решай вместе со мной.

Решаем примеры:Представить в виде многочлена:(x+4)(x-4)=x2-16( 3-m)(3+m)=9-m2(8+y)(y-8)=y2-64II. Разложить на множители:с2-25=(с-5)(с+5)81-p2=(9+p)(9-p)0,36-y2=(0,6-y)(0,6+y)

Предлагаю вам примеры для самостоятельного решения: (3x+4)(3x-4)=(2-5n)(5n+2)=(7с2+4x)(4x-7c2)=81p2-16a2=25-36b4d2=0,49a6-1=9x2-164-25n216x2-49c4(9p+4a)(9p-4a)(5-6b2d)(5+6b2d)(0,7a3-1)(0,7a3+1) Нажми любую клавишу и появятся ответы для самопроверки.

Быстрый счётА я догадался, как можно использовать эту формулу для быстрых вычислений.Смотри и учись.292-282=(29-28)(29+28)=1·57=57732-632=(73+63)(73-63)=136·10=13601332-1342=(133-134)(133+134)= -1·267= -267

А сейчас я предлагаю вам познакомиться с задачей Пифагора.

Задача Пифагора «Всякое нечётное число, кроме единицы, есть разность двух квадратов.»Решение задачи:(n+1)2-n2=(n+1-n)(n+1+n)=2n+1- получили нечётное числоВ школе Пифагора эта задача решалась геометрически. Действительно, если от квадрата отнять гномон, представляющий нечётное число элементарных квадратов, составляющих полный законченный ряд (на рис. выделено цветом), то в остатке получится квадрат, т.е.2n+1=(n+1)2-n2

Вот и завершается наш урок.На этом уроке вы, ребята, познакомились с формулами сокращенного умножения, рассмотрели два способа доказательства этих формул, а также примеры их применения.Вам были предложены упражнения для решения и вы могли проверить себя.Я только хочу вам напомнить, что при решении задач, упражнений на применение формул нужно искать различные подходы, разнообразные способы. До свидания.