Презентация на тему: Система уравнений

Система уравнений Система – это закономерно связанные друг с другом элементы представляющие единство (Словарь Лопатухина) Система – целое, составленное из частей System – объединение Система – это порядок Решить систему уравнений – применить систему знаний Нет системы - нет порядка

Цель: Обобщить понятие решения системы уравнений Задачи: Применять основные методы решения систем уравнений, различного уровня сложности Уметь создавать презентации для сопровождения доклада и буклеты Применять умения работать на компьютере при решении систем уравнений графическим способом

Рассмотрим системы уравнений и определим наиболее эффективный метод решения

Решим систему методом подстановки: 1.Выразим х из (2) х=1+у 2.Подставим в (1) (1+у)у=12 х=1+у 3. Решим (1) (1+у)у=12 у2+у=12 у2+у=12 у2-у-12=0 Д=в2-4ас Д=(-1)2-4*1*(-12)=1+48=49 Д>0 4. Значит мы получили 2-е системы у=4 или у=-3 х=1+у х=1+у у=4 у=-3 х=1+4 х=1-3 у=4 у=-3 х=5 х=-2 ответ:(5; 4) (-2;-3)

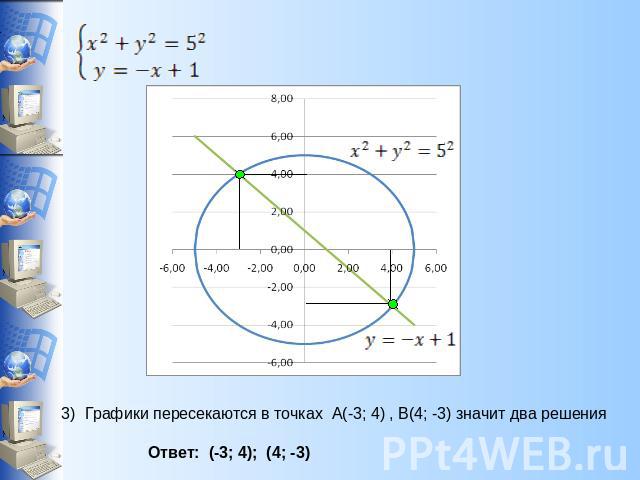
Решение системы уравнений графическим методом 2) В одной системе координат построим графики данных уравнений. б) y=-x+1 (прямая, проходящая через (0;1) и (1;0))

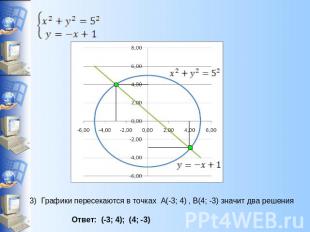
Графики пересекаются в точках А(-3; 4) , В(4; -3) значит два решения Ответ: (-3; 4); (4; -3)

Решение системы уравненийметодом сложения Ответ: (4; 1) и (-4; 1)

Решение системы уравненийметод введения новой переменой 1). Введем новые переменные, обозначив так: пусть x+y=a хy=b 2). Получим 3). По теореме обратной теореме Виета 4). Значит система примет вид

5). Применим подстановку 6). Решим уравнения с одной переменной D=1 – 4 * 6 = -23, D<0, нет корней