Презентация на тему: Звёздчатые формы многогранников

ЗВЕЗДЧАТЫЕ МНОГОГРАННИКИ Кроме правильных и полуправильных многогранников, красивые формы имеют, так называемые, звездчатые многогранники. Здесь мы рассмотрим правильные звездчатые многогранники. Их всего четыре. Первые два были открыты И. Кеплером, а два других почти 200 лет спустя построил Л. Пуансо (1777-1859). Именно поэтому правильные звездчатые многогранники называются телами Кеплера-Пуансо. Они получаются из правильных многогранников продолжением их граней или ребер. 900igr.net

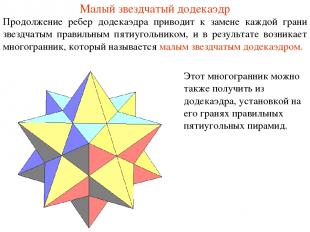
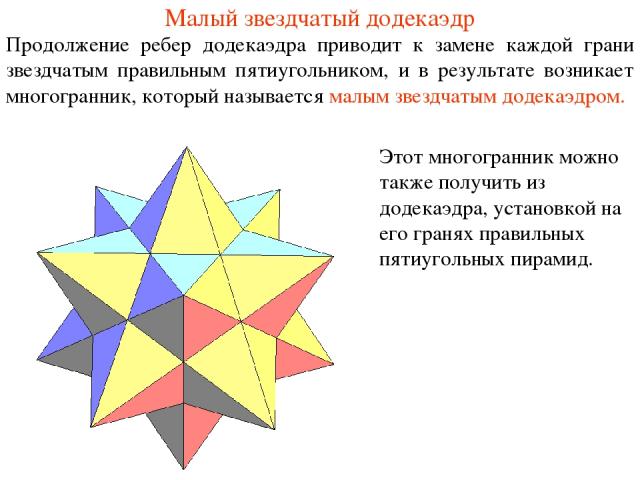
Малый звездчатый додекаэдр Продолжение ребер додекаэдра приводит к замене каждой грани звездчатым правильным пятиугольником, и в результате возникает многогранник, который называется малым звездчатым додекаэдром. Этот многогранник можно также получить из додекаэдра, установкой на его гранях правильных пятиугольных пирамид.

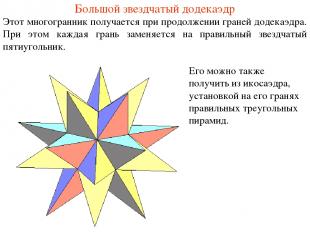
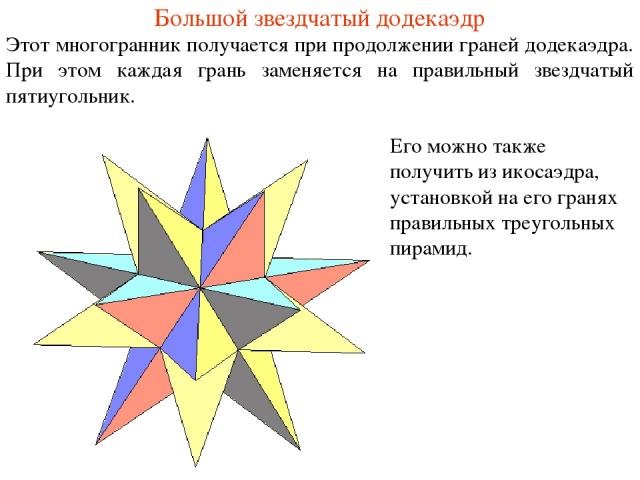
Большой звездчатый додекаэдр Этот многогранник получается при продолжении граней додекаэдра. При этом каждая грань заменяется на правильный звездчатый пятиугольник. Его можно также получить из икосаэдра, установкой на его гранях правильных треугольных пирамид.

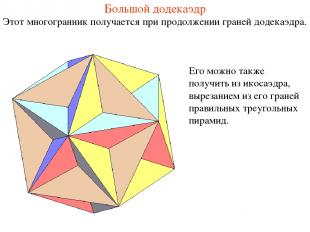
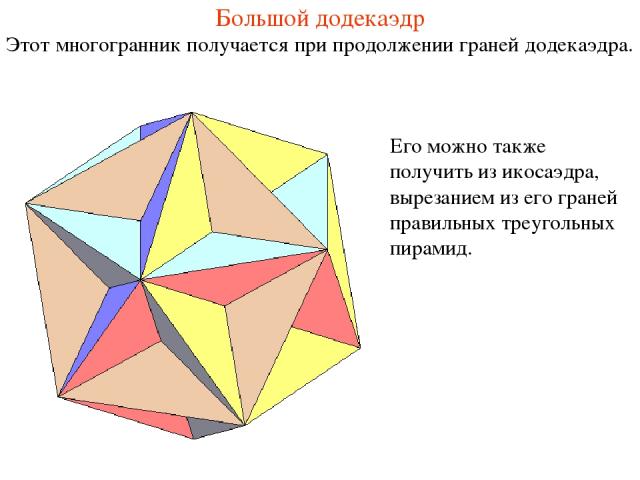
Большой додекаэдр Этот многогранник получается при продолжении граней додекаэдра. Его можно также получить из икосаэдра, вырезанием из его граней правильных треугольных пирамид.

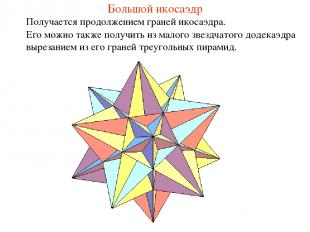
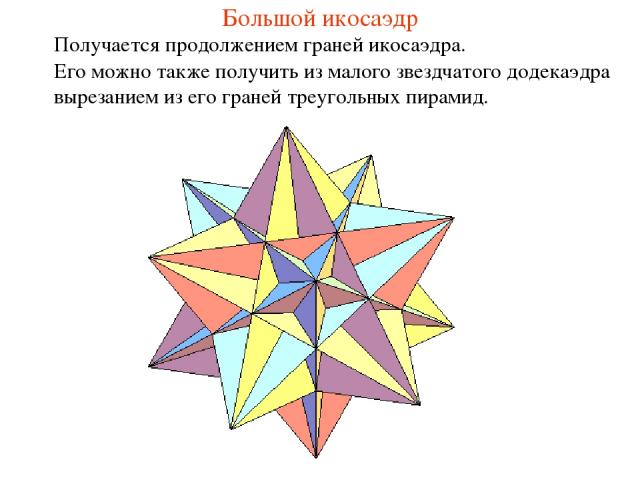
Большой икосаэдр Получается продолжением граней икосаэдра. Его можно также получить из малого звездчатого додекаэдра вырезанием из его граней треугольных пирамид.

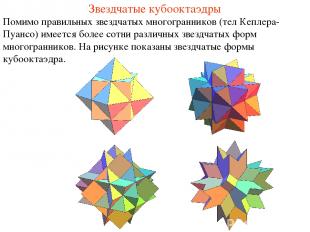
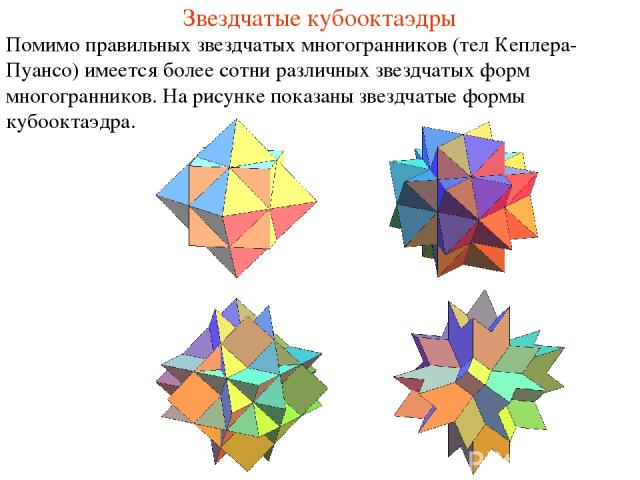
Звездчатые кубооктаэдры Помимо правильных звездчатых многогранников (тел Кеплера-Пуансо) имеется более сотни различных звездчатых форм многогранников. На рисунке показаны звездчатые формы кубооктаэдра.

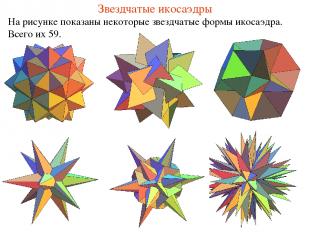
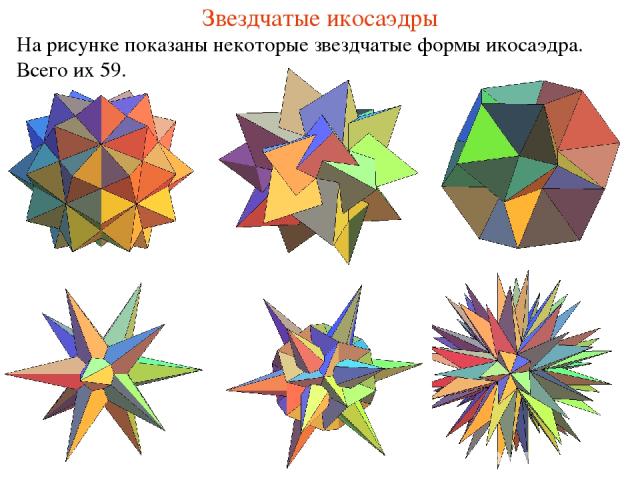
Звездчатые икосаэдры На рисунке показаны некоторые звездчатые формы икосаэдра. Всего их 59.

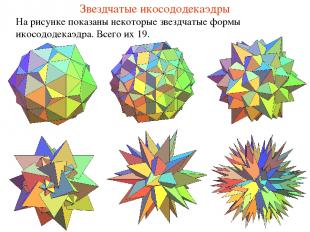
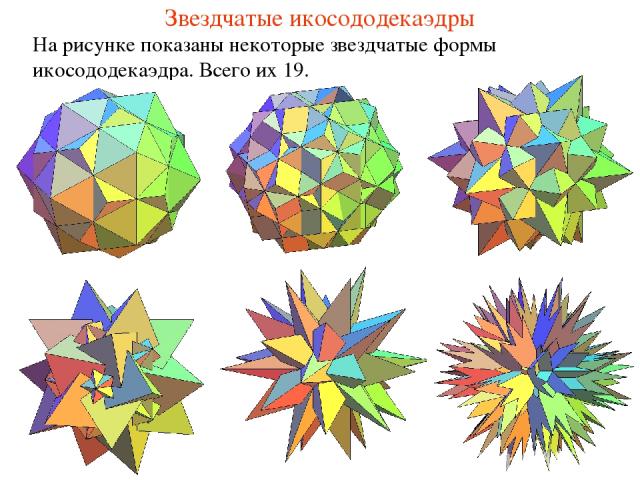
Звездчатые икосододекаэдры На рисунке показаны некоторые звездчатые формы икосододекаэдра. Всего их 19.

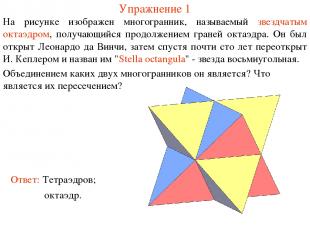
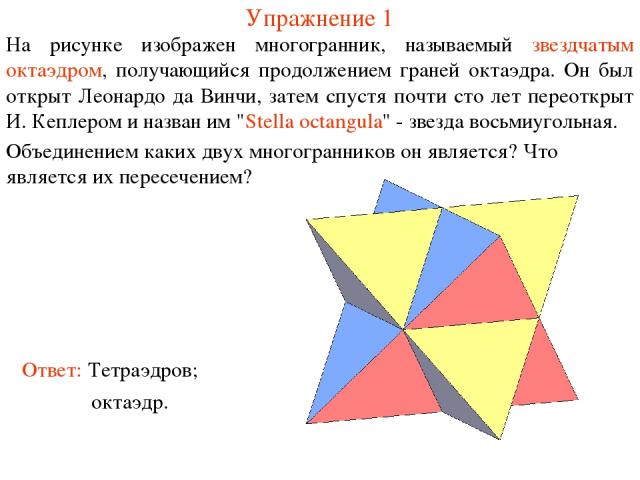
Упражнение 1 На рисунке изображен многогранник, называемый звездчатым октаэдром, получающийся продолжением граней октаэдра. Он был открыт Леонардо да Винчи, затем спустя почти сто лет переоткрыт И. Кеплером и назван им "Stella octangula" - звезда восьмиугольная. Ответ: Тетраэдров; Объединением каких двух многогранников он является? Что является их пересечением? октаэдр.

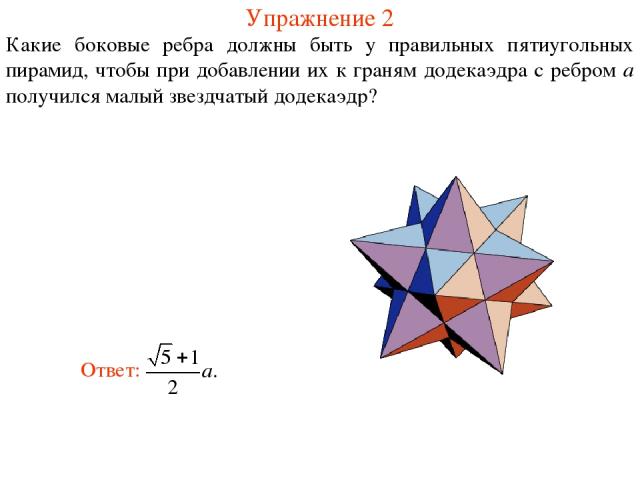
Упражнение 2 Какие боковые ребра должны быть у правильных пятиугольных пирамид, чтобы при добавлении их к граням додекаэдра с ребром a получился малый звездчатый додекаэдр?

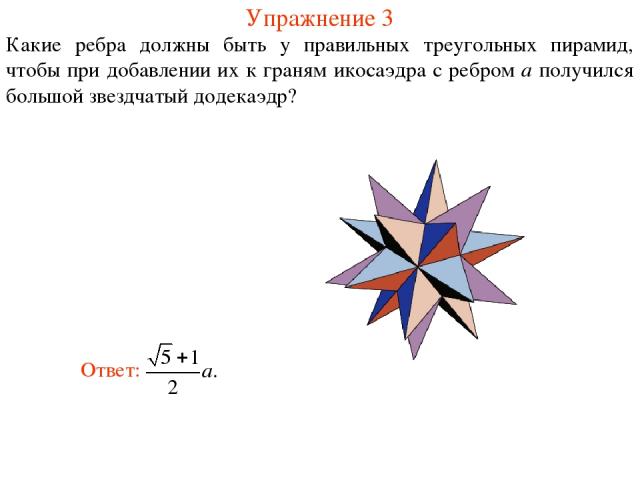
Упражнение 3 Какие ребра должны быть у правильных треугольных пирамид, чтобы при добавлении их к граням икосаэдра с ребром a получился большой звездчатый додекаэдр?

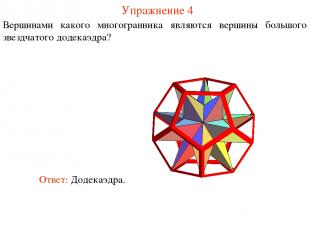
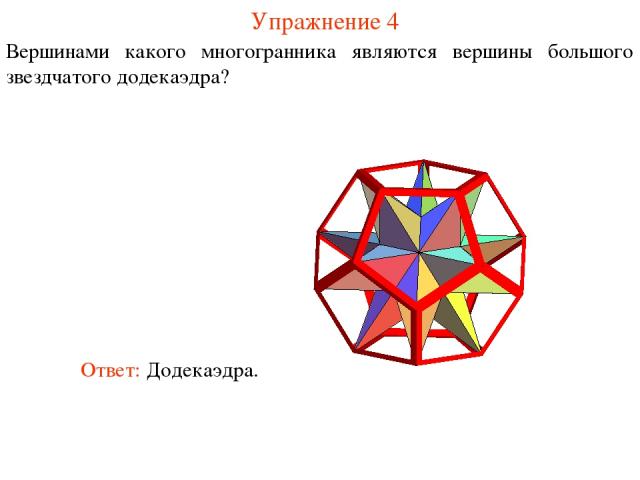
Упражнение 4 Вершинами какого многогранника являются вершины большого звездчатого додекаэдра?

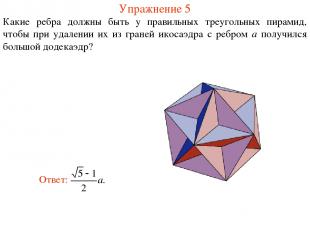
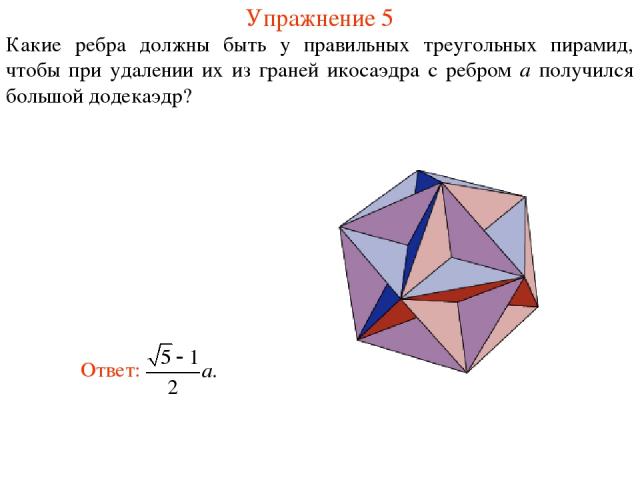
Упражнение 5 Какие ребра должны быть у правильных треугольных пирамид, чтобы при удалении их из граней икосаэдра с ребром a получился большой додекаэдр?

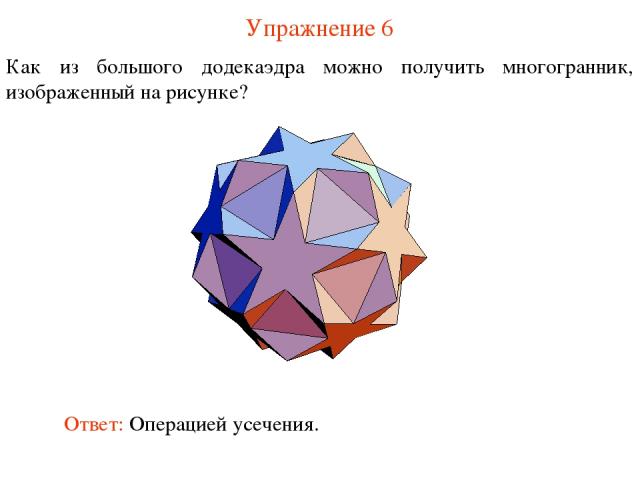
Упражнение 6 Как из большого додекаэдра можно получить многогранник, изображенный на рисунке? Ответ: Операцией усечения.

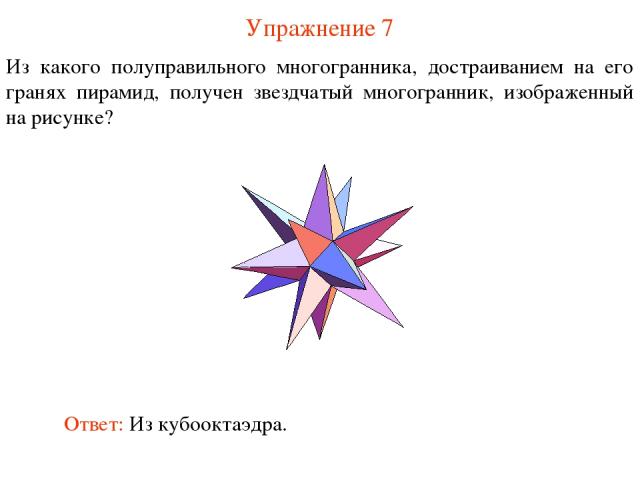
Упражнение 7 Из какого полуправильного многогранника, достраиванием на его гранях пирамид, получен звездчатый многогранник, изображенный на рисунке? Ответ: Из кубооктаэдра.

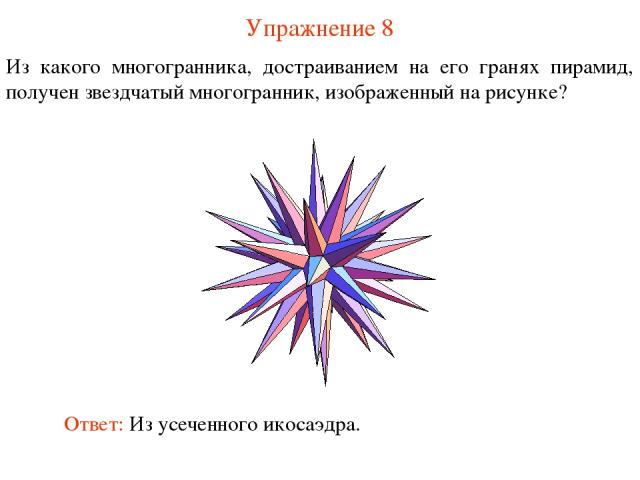
Упражнение 8 Из какого многогранника, достраиванием на его гранях пирамид, получен звездчатый многогранник, изображенный на рисунке? Ответ: Из усеченного икосаэдра.

Упражнение 9 На рисунке показан звездчатый усеченный икосаэдр, полученный из усеченного икосаэдра достраиванием на его гранях пирамид. Сколько у него вершин (В), ребер (Р) и граней (Г)? Ответ. В = 92; Р = 270; Г = 180.

Упражнение 10 На рисунке показан многогранник, полученный усечением звездчатого усеченного икосаэдра. Сколько у него вершин (В), ребер (Р) и граней (Г)? Ответ. В = 540; Р = 810; Г = 272.

Упражнение 11 На рисунке показан многогранник, полученный из усеченного звездчатого усеченного икосаэдра достраиванием на его гранях правильных пирамид. Сколько у него граней? Ответ. 1690.