Презентация на тему: Задачи по геометрии на теорему Пифагора

ТЕОРЕМА ПИФАГОРА Уделом истины не может быть забвенье, Как только мир ее увидит взор, И теорема та, что дал нам Пифагор, Верна теперь, как в день ее рожденья. Шамиссо 900igr.net

Цель урока Учебно – познавательная: Обобщение и расширение знаний учащихся по данной теме; Формирование умений применять теорему Пифагора в стандартных и нестандартных ситуациях; Знакомство с историей возникновения теоремы Развитие познавательного интереса у учащихся через решение нестандартных , исторических задач

Цель урока развивающая: Развитие умений самостоятельно работать с дополнительной литературой, применять Интернет технологии, создавать компьютерные презентации, проводить отбор необходимого для урока материала ; Развитие грамотной математической речи; Проведение самооценки учебной деятельности воспитательная: воспитание настойчивости и трудолюбия

ТЕОРЕМА ПИФАГОРА Обобщающий урок

План урока Опрос по теории Решение задач по готовым чертежам ( устно) Историческая справка о жизни Пифагора ( презентация) История теоремы Пифагора ( презентация) Самостоятельное решение задач по готовым чертежам (самооценка) Решение исторических и практических задач ( работа в группах) Значение теоремы Пифагора ( презентация ) Подведение итогов урока Домашнее задание

Опрос по теории Для какого треугольника справедлива теорема Пифагора? Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника? Дайте определение гипотенузы Дайте определение катета Сформулируйте теорему Пифагора и теорему обратную теореме Пифагора

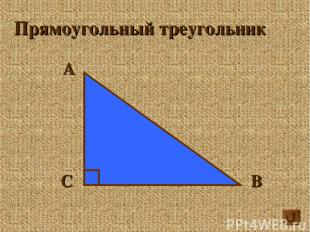
А В С Прямоугольный треугольник

А С В Определение Треугольник, в котором один из углов прямой называется прямоугольным

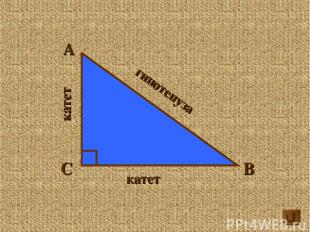
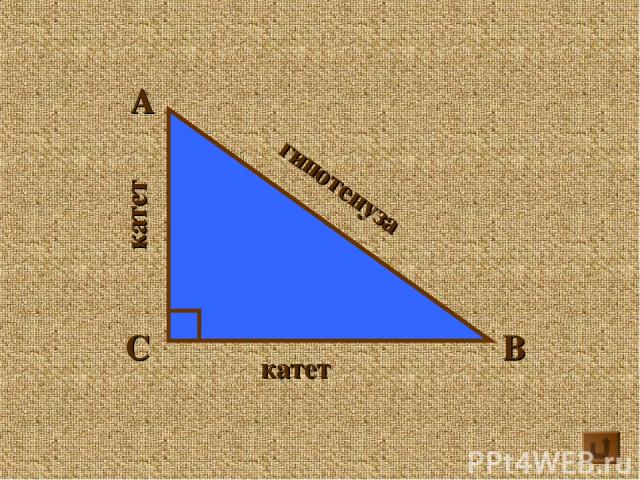
А В С катет катет гипотенуза

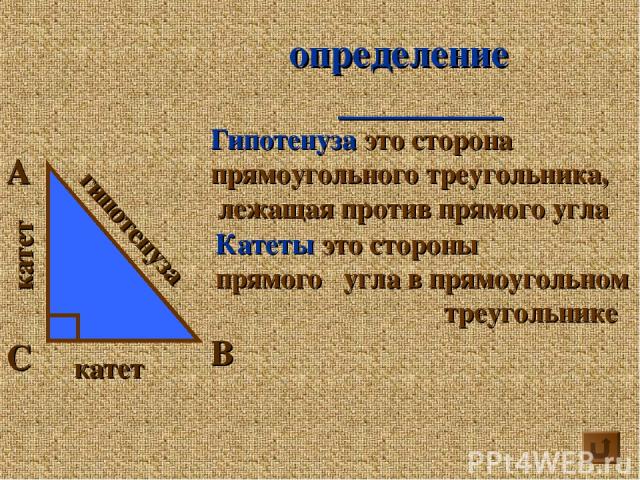
А В С катет катет гипотенуза определение Гипотенуза это сторона прямоугольного треугольника, лежащая против прямого угла Катеты это стороны прямого угла в прямоугольном треугольнике

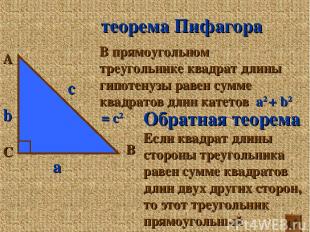
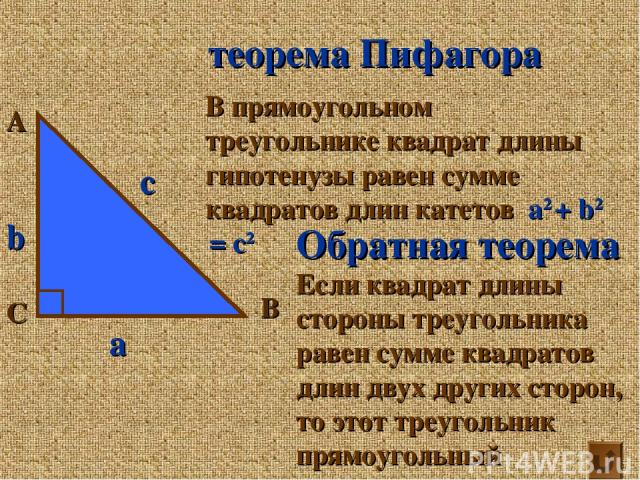
А С В теорема Пифагора В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов а2 + b2 = с2 Обратная теорема Если квадрат длины стороны треугольника равен сумме квадратов длин двух других сторон, то этот треугольник прямоугольный а b c

Задача 1 А Н К С Р Задача2 45° Задачи по готовым чертежам ? 5 А 45° ? K 7 M

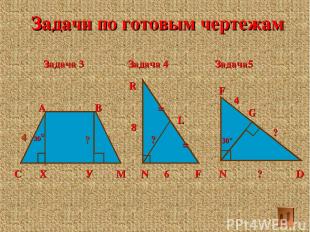
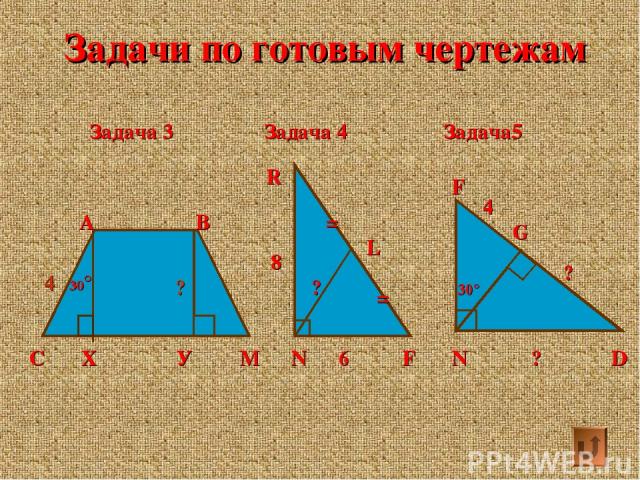
Задачи по готовым чертежам Задача 3 Задача 4 Задача5 С Х У М А В 30° R 8 N 6 F L ? = = 30° F N ? D G ? 4 4 ?

Пифагор Великий ученый Пифагор родился около 570 г. до н.э. в Древней Греции на острове Самосе, поэтому его называют Пифагором Самосским.. По многим свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.

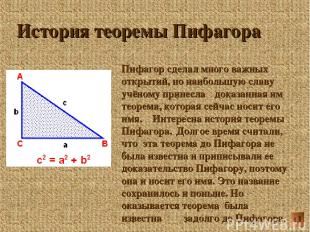
История теоремы Пифагора Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя. Интересна история теоремы Пифагора.. Долгое время считали, что эта теорема до Пифагора не была известна и приписывали ее доказательство Пифагору, поэтому она и носит его имя. Это название сохранилось и поныне. Но оказывается теорема была известна задолго до Пифагора.

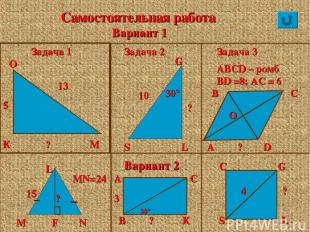
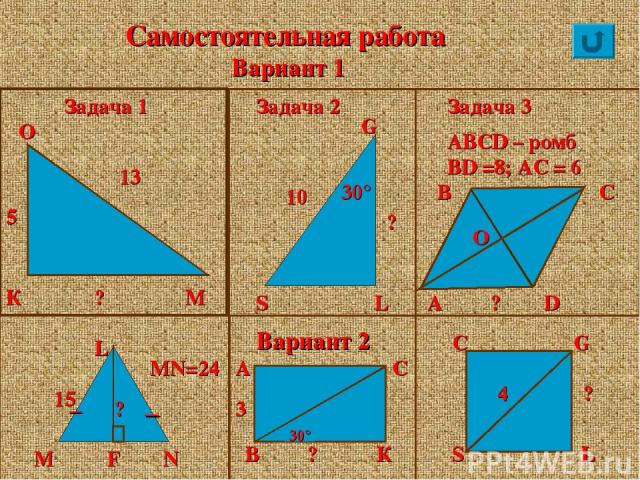
Самостоятельная работа Вариант 1 Задача 1 О М К 13 Задача 2 ? 5 10 ? 30° S L G Задача 3 В А ? D С ABCD – ромб, BD =8; АС = 6 Вариант 2 М F N L 15 ? _ _ MN=24 В ? К А С 3 S L C G 4 ? О 30°

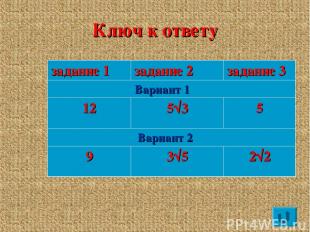
Ключ к ответу задание 1 задание 2 задание 3 Вариант 1 12 5√3 5 Вариант 2 9 3√5 2√2

1.Задача индийского математика XII века Бхаскары На берегу реки рос тополь одинокий. Вдруг порыв ветра его ствол надломил. Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у самой реки. Осталось три фута всего от ствола. Прошу тебя скоро теперь мне скажи: « У тополя как велика высота?»

1.Решение задачи Бхаскары С А 4 М В • - - 3 Дано: АМС – прямоугольный АС = 3 фута АМ = 4 фута Найти: АВ Решение: СМ=СВ ( по условию) СМ2 = АМ2 + АС2; СМ2 = 42 + 32 СМ2 = 16+9 СМ2 = 25 СМ = 5 (ф) ≈244см( 1фут ≈ 30,5 см)

2. Практическая работа Землемеры Древнего Египта для построения прямого угла использовали бечевку, разделенную узлами на 12 равных частей. Покажите как они это делали. ●

Выполнение практической работы • • • • • • • • • • • • 3 4 5 52 = 32 + 42

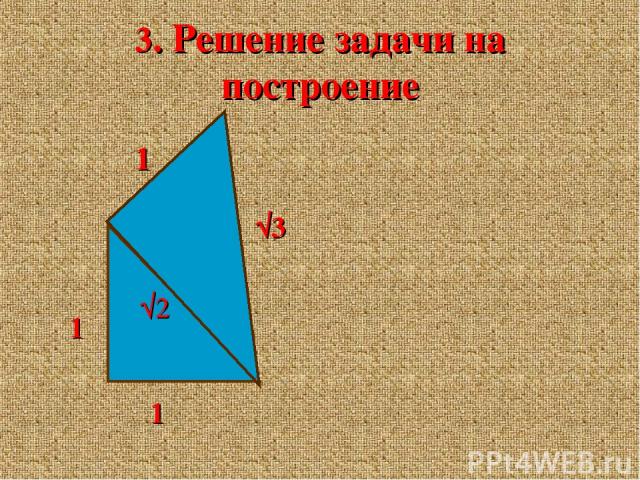
3. Задача на построение Как, используя теорему Пифагора, построить отрезок длиной √2, √3 ?

3. Решение задачи на построение 1 1 √2 1 √3

4. Задача древних индусов Над озером тихим, С полфута размером, Высился лотоса цвет. Он рос одиноко. И ветер порывом Отнес его в сторону. Нет боле цветка над водой. Нашел же рыбак его Ранней весной В двух футах от места, где рос Итак: предложу я вопрос: Как озера вода здесь глубока?

Решение задачи древних индусов 0,5 ф 2 ф Х Х+ 0,5 А В С К . АК – длина лотоса Т.к. лотос отклонился, то АК = АС Пусть АВ=Х Треугольннк АВС – прямоугольный. АС2 = СВ2 + АВ2 (Х+ 0,5)2=22 + Х2 Х2+ Х + 0,25 = 4 +Х2 Х = 3,75( ф) Ответ: глубина озера 3,75 футов, длина камыша 4,25 футов

5. Задача Диагональ телевизионного экрана 50 см, длины его сторон относятся как 3:4. Чему равны длины сторон экрана? Войдет ли телевизор в нишу стенки, если размеры этой ниши 49см х 35см?

Решение задачи № 5 Пусть х см –длина одной части, тогда 3х см- длина одной стороны, 4х см – длина другой стороны. По теореме Пифагора имеем: (3х)2 + (4х)2 =2500 25х2 = 2500 х2 = 100 х= 10 3х = 30(см) – длина одной стороны 4х =40см - длина втоорой стороны Ответ: размеры телевизора подходят.

Значение теоремы Пифагора Теорема Пифагора- это одна из главных и, можно сказать , самая главная теорема геометрии. Ее можно применять для построения отрезков, длины которых заданы иррациональным числом; можно строить прямые углы подобно тому, как это делали египтяне при строительстве древних сооружений; в различных областях человеческой деятельности.

Значение теоремы Пифагора В конце 19 века высказывались предположения о существовании обитателей Марса подобных человеку.. Было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал

Дополнительные задачи « Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: каковаглубина воды и какова длина камыша?». Задача № 1 (Задача из китайской «Математики в девяти книгах» )

Дополнителььные задачи Задача №2 ( Задача из учебника «Арифметика» Леонтия Магницкого) «Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».

Домашнее задание Доказать теорему Пифагора несколькими способами; Придумать задачи практического содержания, решение которых предполагает использование теоремы Пифагора Подобрать исторические задачи (1, 2) Решить одну из исторических задач; Найти слова поэтов, ученых о теореме Пифагора ( 1, 2) Подготовить презентацию или буклет по одному из выше перечисленных буклетов

О теореме Пифагора Немецкий писатель-романист А. Шамиссо, написал следующие стихи. Пребудет вечно истина, как скоро Её познает слабый человек! И ныне теорема Пифагора Верна, как и в его далекий век.   Обильно было жертвоприношенье Богам от Пифагора. Сто быков. Он отдал на закланье и сожженье За сета луч, пришедший с облаков.   Поэтому всегда с тех самых пор, Чуть истина рождается на свет, Быки ревут, ее почуя вслед, От страха что вселил в них Пифагор.

О теореме Пифагора Уделом истины не может быть забвенье, Как только мир ее увидит взор, И теорема та, что дал нам Пифагор, Верна теперь, как в день ее рожденья. За светлый луч с небес вознес благодаренье Мудрец богам не так, как было до тех пор. Ведь целых сто быков послал он под топор, Чтоб их сожгли как жертвоприношенье. Быки с тех пор, как только весть услышат, Что новой истины уже следы видны, Отчаянно мычат и ужаса полны: Им Пифагор навек внушил тревогу. Не в силах преградить той истине дорогу, Они, закрыв глаза, дрожат и еле дышат. (А. фон Шамиссо, перевод Хованского)

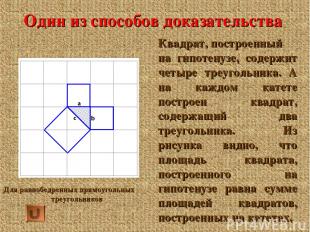
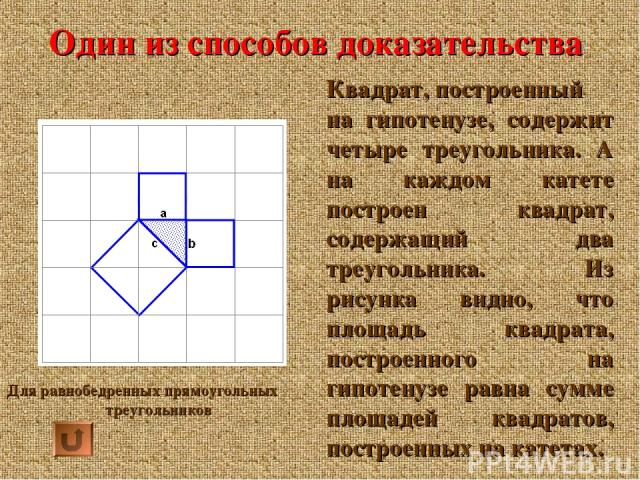
Один из способов доказательства Квадрат, построенный на гипотенузе, содержит четыре треугольника. А на каждом катете построен квадрат, содержащий два треугольника. Из рисунка видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах. Для равнобедренных прямоугольных треугольников

Спасибо за внимание! Учитель математики Одинцовской гимназии №13 Попова А.А.