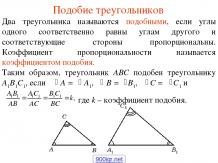
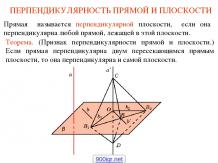
Презентация на тему: Задачи на прямоугольный треугольник

Тема: Применение свойств и признаков равенства прямоугольных треугольников к решению практических задач. (Урок геометрии – 7 класс)   Цель: показать практическое применение свойств и признаков равенства прямоугольных треугольников к решению практических задач; познакомить с историей развития некоторых математических идей, их влияние на жизнь современного общества; Развивать интуицию, способность ориентироваться в новых ситуациях, стремление к применению полученных знаний, воспитывать уважение к значимости полученных знаний.   900igr.net

«Сближение теории с практикой даёт самые благотворные результаты, и не одна только практика от этого выигрывает». П.А. Чебышев

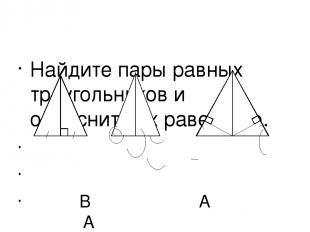
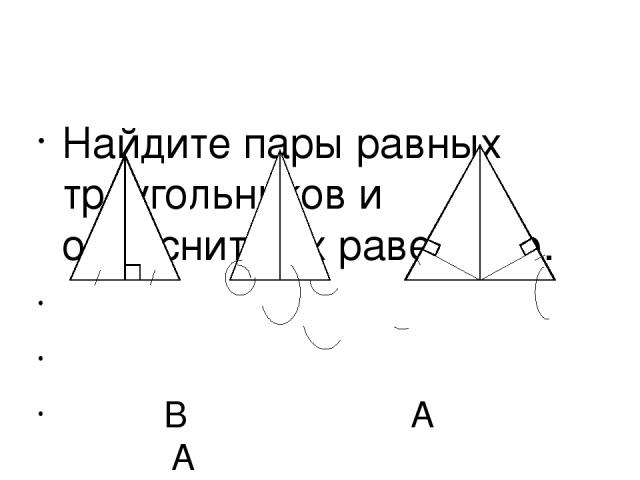
Найдите пары равных треугольников и объясните их равенство.     В А А             D E   C А D C C D B C M B     AD = DC < C =

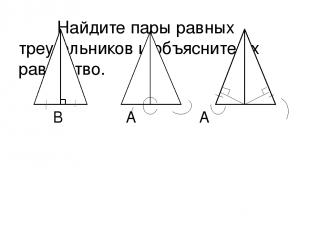
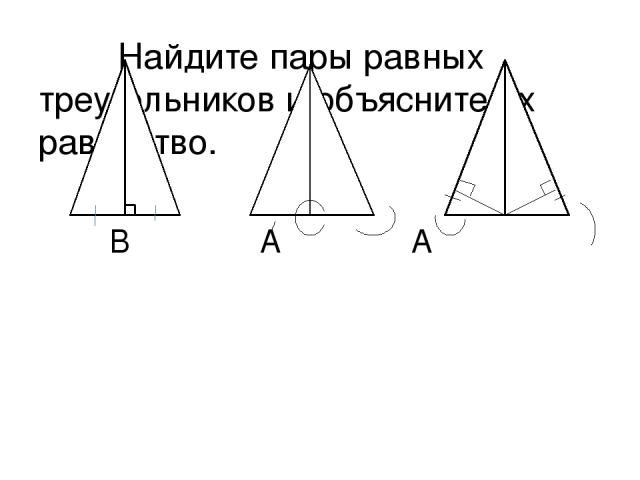
Найдите пары равных треугольников и объясните их равенство. В А А Е D А D С С D В В М С АD = СD < C =

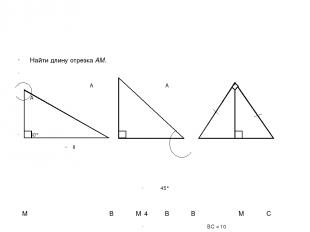
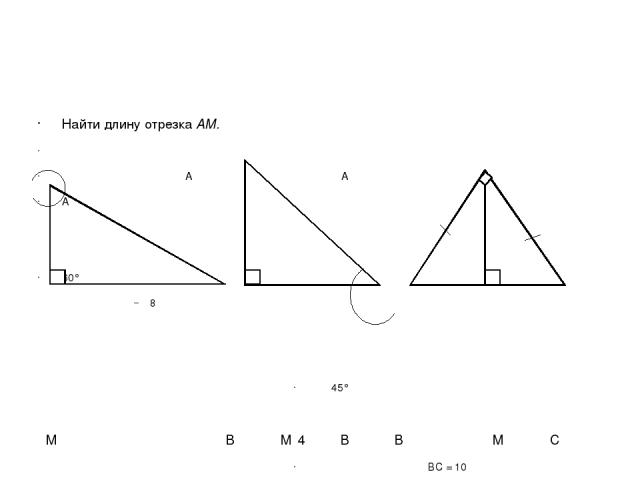
Найти длину отрезка АМ.     A A  A 60° 8 45° M B M 4 B B M C BC = 10

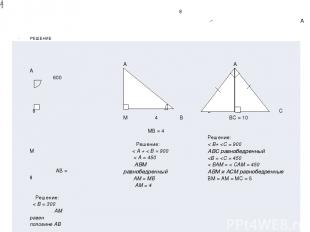
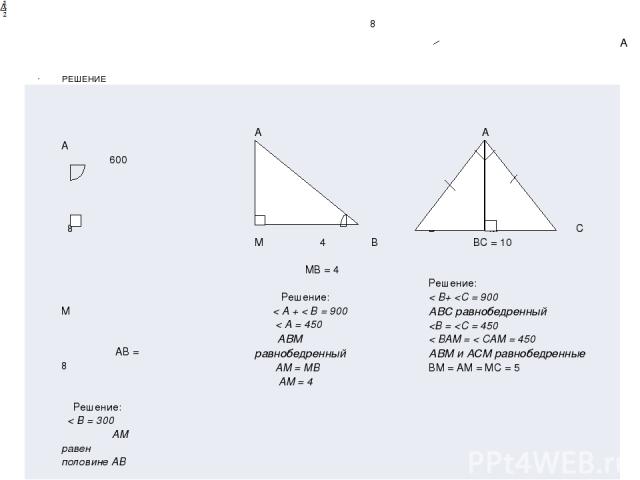
РЕШЕНИЕ A 8 А 600 8 М АВ = 8 Решение:

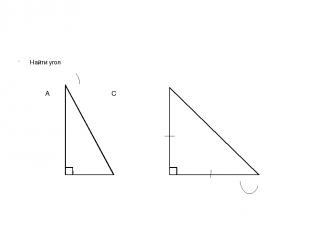
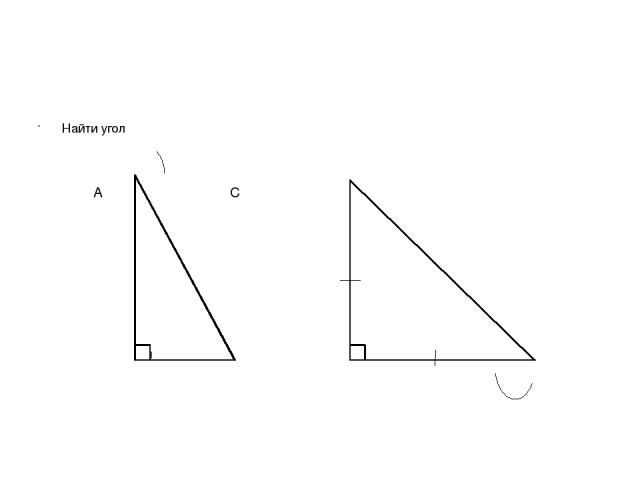
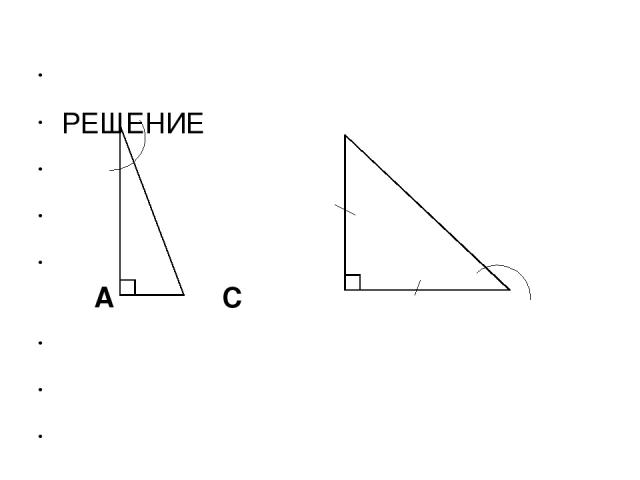
Найти угол α А С α 8 α С 4 В В А

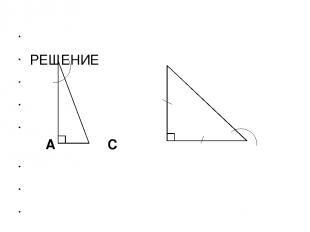
α   РЕШЕНИЕ     А С   α     8     α     С 4 В В А   СВ равен половине АВ Треугольник АВС равнобедренный α = 300 СВ = АВ

II. Самостоятельная работа (работа в группах). За решение каждой задачи пять баллов Карточки с заданиями лежат на партах     1. Доказать, что точка биссектрисы угла равноудалена от его сторон.   2. Доказать, что каждая точка, равноудалённая от сторон угла, лежит на его биссектрисе.  

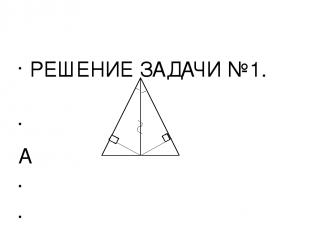
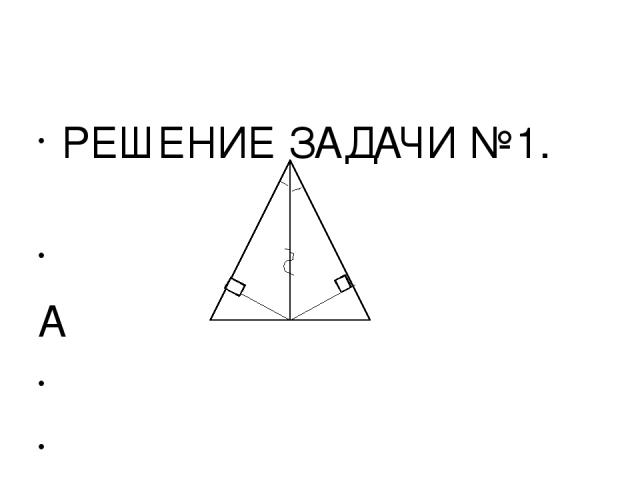
РЕШЕНИЕ ЗАДАЧИ №1. А                   М D   В О С   треугольники АMO и ADO прямоугольные(< ОМА и < ОDА прямые), они равны по гипотенузе и острому углу, так как < МАО = < DАO (AO- биссектриса угла ВАС) АО общая сторона Из равенства треугольников следует равенство отрезков МО и ОD    

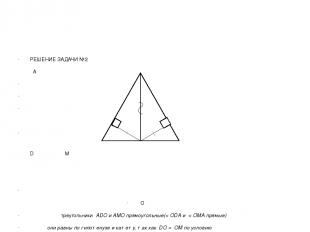
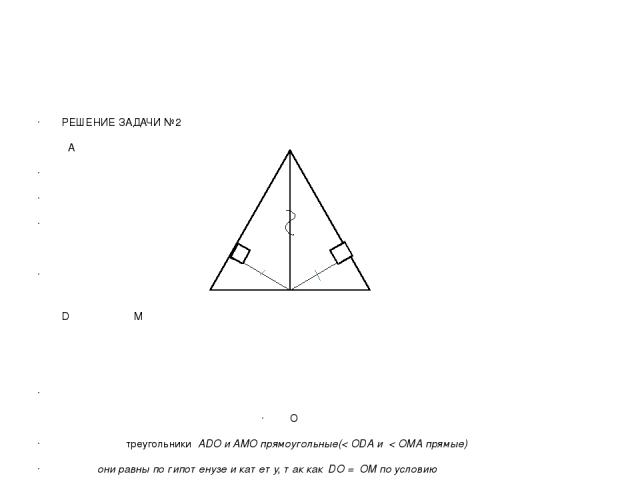
РЕШЕНИЕ ЗАДАЧИ №2 А        D M   O треугольники АDO и AMO прямоугольные(< ОDА и < ОMА прямые) они равны по гипотенузе и катету, так как DО = ОM по условию АО общая сторона Из равенства треугольников следует равенство углов DАО и ОАM. Значит АО - биссектриса 

III. Решение практических задач. (Задания написаны на карточках) 1. Населённые пункты A, B, C, D расположены так, что пункт А находится в нескольких километрах к югу от D, а пункты В и С – на одинаковых расстояниях к западу и востоку (соответственно) от А. Верно ли, что В и С находятся на одинаковом расстоянии от D?  

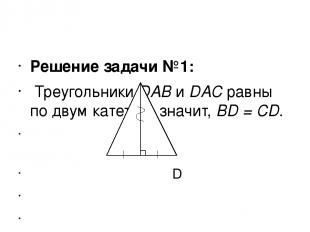
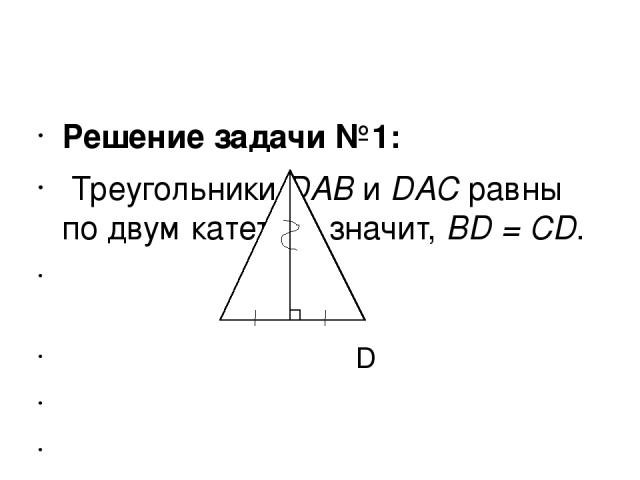
Решение задачи №1: Треугольники DAB и DAC равны по двум катетам, значит, BD = CD.       D                         В А С ОТВЕТ: верно    

2. Жители трёх домов (A, B. C) , расположенных в вершинах равнобедренного прямоугольного треугольника хотят выкопать общий колодец с таким расчётом, чтобы он был одинаково удалён от всех домов. В каком месте надо копать?

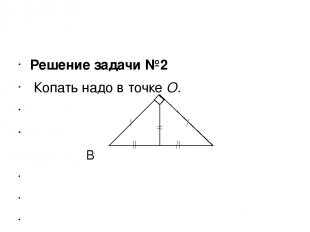
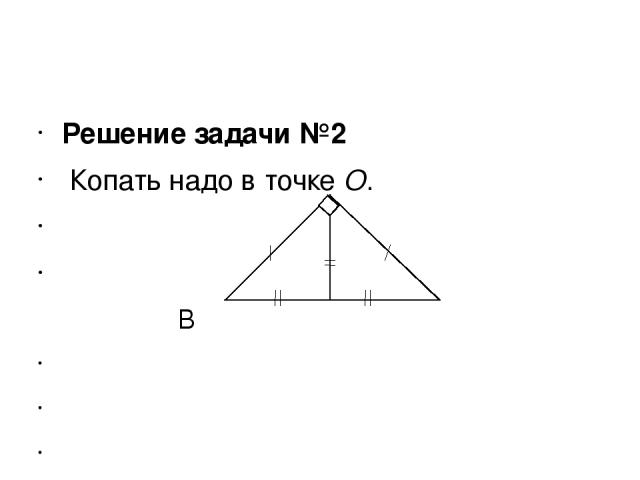
Решение задачи №2 Копать надо в точке О.       В               А O C        

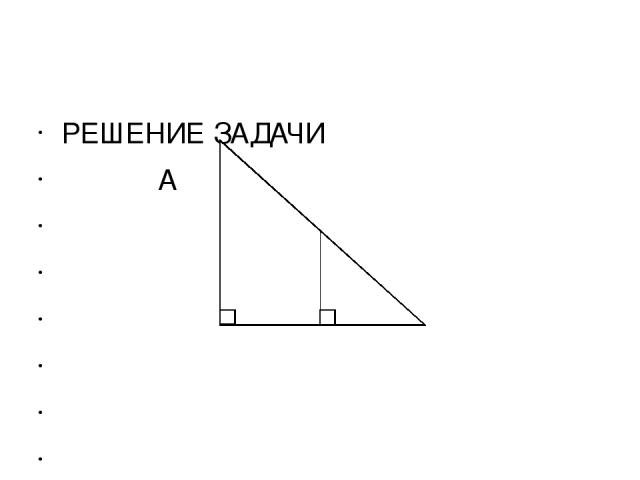
Задачи Фалеса: а) Египтяне задали Фалесу трудную задачу: найти высоту одной из громадных пирамид. Фалес нашёл для этой задачи простое и красивое решение. Он воткнул в землю вертикально длинную палку и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды.

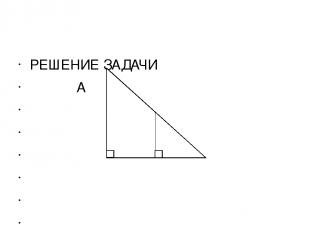
РЕШЕНИЕ ЗАДАЧИ   A               A,                 C  C, B   Треугольник АСВ – равнобедренный АС = СВ Треугольник А1С1В – равнобедренный А1С1 = С1В.  

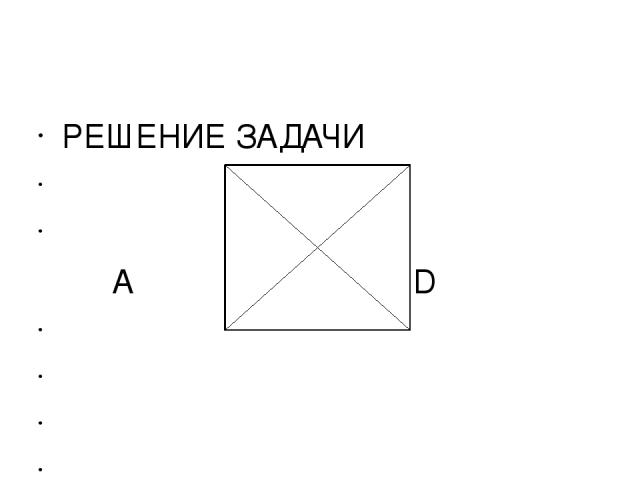
б) Ещё одно из свойств прямоугольного треугольника, доказанное Фалесом. Нарисуем прямоугольный треугольник АВС и разделим его гипотенузу АС точкой О пополам. Как вы думаете, какой отрезок длиннее: АО или ОВ? То есть куда ближе идти из середины гипотенузы – к острому углу или к прямому?

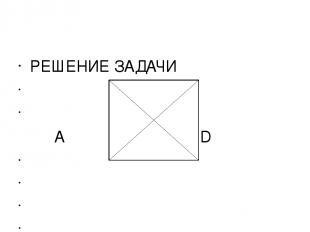
РЕШЕНИЕ ЗАДАЧИ     А  D               o   C B   Достроим треугольник АСВ до прямоугольника ADBC. AB = DC и точка О – середина каждого из них. Следовательно, АО = ОВ = ОС.  

IV. Компьютерная презентация. Биография Фалеса Существовало предание, что Фалес был финикийцем, ставший гражданином Милета. Фалес Милетский жил в самом конце VII - первой половине VI в. до н. э. (с. 625 – 548 до н. э.). Фалес Милетский был уроженцем греческого торгового города Милета, расположенного в Малой Азии на берегу Эгейского моря. В VI веке до н. э. Милет находился в расцвете славы. Это был многолюдный и шумный город купцов, торговцев, ремесленников, мореплавателей. Жемчужиной Эллады называли его и греки, и чужестранцы. Как рассказывают древние историки, в четырёх гаванях города встречались корабли, прибывшие из Сирии, Финикии, Египта, Крита. Главная гавань называлась Львиной. Узкий вход в неё охраняли два огромных мраморных льва. На широкой набережной толпились носильщики, матросы, менялы, проводники. Вся эта шумная толпа набрасывалась на чужеземцев, прибывших в Милет, предлагая услуги. От огромных ворот порта с шестнадцатью мраморными кодонами вела в город широкая главная улица. Милет – родина Фалеса. Неподалёку от ворот стоял величественный храм Аполлона с мраморными жертвенниками и статуями. Но купцов, прибывших из разных стран в Милет, привлекали не только красоты города. Тончайшая шерсть из милетских овец славилась всюду. Садоводы Милета выводили прекрасные сорта роз. Из лепестков роз изготовляли драгоценное розовое масло. Окрестности города утопали в густых оливковых садах. В далёкие путешествия отправлялись милетские торговцы-моряки. Эти путешествия были опасны. Порой приходилось бороться с разбушевавшейся стихией, обороняться от пиратов, а при высадке на сушу отражать нападения туземцев. Но не только мужества требовала жизнь от тогдашних мореплавателей. Она требовала ещё и умения ответить на многие вопросы. Как ориентироваться в море? Как определить расстояние от берега до корабля? Тесная зависимость жизненного успеха людей от решения теоретических вопросов привела к тому, что город Милет стал колыбелью античной науки, а учёный Фалес – её родоначальником. «Ищи что-нибудь одно мудрое, выбирай что-нибудь одно доброе, так ты уймёшь пустословие болтливых людей». Фалес был купцом. Он хорошо зарабатывал, умело торгуя оливковым маслом. Много путешествовал: посетил Египет, Среднюю Азию, халдею. Всюду изучал опыт, накопленный жрецами, ремесленниками и мореходами: познакомился с египетской и вавилонской школами математики и астрономии. Возвратившись на родину, Фалес отошел то торговли и посвятил свою жизнь занятиями наукой, окружив себя учениками, - так образовывалась милетская ионийская школа, из которой вышли многие знаменитые греческие учёные. Фалес дожил до глубокой старости.

  Вклад в науку Фалес Милетский имел титул одного из семи мудрецов Греции, он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции, -- он был тем же для Греции, чем Ломоносов для России. Карьеру он начал как купец и еще в молодости попал в Египет. В Египте Фалес застрял на много лет, изучая науки в Фивах и Мемфисе. Считается, что геометрию и астрономию в Грецию привез он. Во всяком случае, одному у него могут поучиться все философы – краткости. Полное собрание его сочинений, по преданию, составляло всего 200 стихов. Трудно сейчас сказать, что в научном перечне принадлежит действительно Фалесу и что приписано ему потомками, восхищающимися его гением. Несомненно, в лице Фалеса Греция впервые обрела одновременно философа математика и естествоиспытателя. Не случайно древние причислили его к «великолепной семёрке» мудрецов древности.

Фалес – математик Условно ему приписывают открытие доказательств ряда теорем: - о делении круга диаметром пополам; - о равенстве углов при основании равнобедренного треугольника; - о равенстве вертикальных углов; - один из признаков равенства прямоугольных треугольников и другое.     Задачи Фалеса Фалес открыл любопытный способ определения расстояния от берега до видимого корабля. Доказательством признаков равенства треугольников занимались ещё пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство теоремы о «равенстве» двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников). Одни источники утверждают, что для этого им был использован признак подобия треугольников. Потомки Фалеса обязаны ему тем, что он, пожалуй впервые ввел в науку, и в частности – в математику, доказательство. Известно сейчас, что многие математические правила были открыты много раньше, чем в Греции. Но все – опытным путём. Строго логическое доказательство правильности каких-либо предложений на основании общих приложений, принятых за достоверные истины, было изобретено греками. Характерная и совершенно новая черта греческой математики заключается в постепенном переходе при помощи доказательства от одного предложения к другому. Именно такой характер математике придал Фалес. И даже сегодня, через 25 веков, приступая к доказательству, например, теоремы о свойствах ромба, вы, в сущности, рассуждаете почти так, как это делали ученики Фалеса.  

Домашнее задание: придумать и решить практическую задачу, в которой были бы использованы свойства или признаки равенства прямоугольных треугольников

Спасибо за урок