Презентация на тему: Задачи на площадь круга

Площадь круга Для нахождения площади круга рассмотрим правильные многоугольники, вписанные в соответствующую окружность. При увеличении числа сторон многоугольники приближаются к окружности. Поэтому площадью круга считают число, к которому приближаются площади вписанных правильных многоугольников при увеличении числа их сторон. Теорема. Площадь круга равна половине произведения длины его окружности на радиус. Таким образом, площадь S круга радиуса R вычисляется по формуле 900igr.net

Площадь сектора Круговым сектором, или просто сектором, называется общая часть круга и центрального угла с вершиной в центре этого круга.

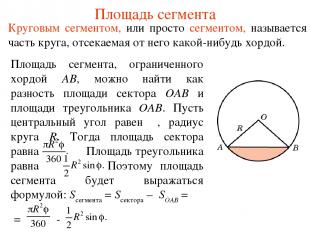
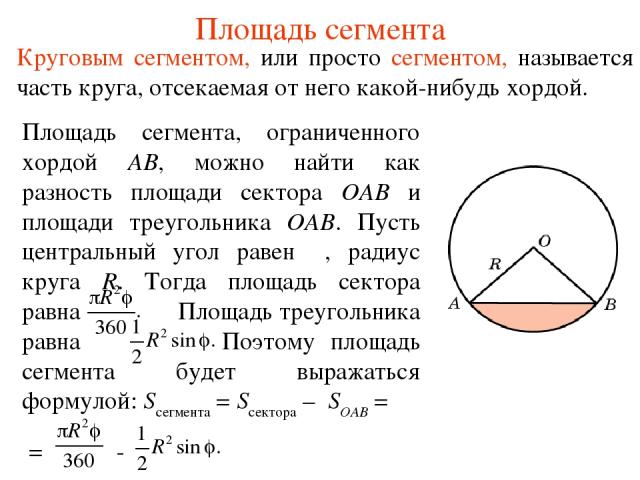
Площадь сегмента Круговым сегментом, или просто сегментом, называется часть круга, отсекаемая от него какой-нибудь хордой. Площадь сегмента, ограниченного хордой AB, можно найти как разность площади сектора OAB и площади треугольника OAB. Пусть центральный угол равен φ, радиус круга R. Тогда площадь сектора равна Площадь треугольника равна Поэтому площадь сегмента будет выражаться формулой: Sсегмента = Sсектора – SOAB = = -

Вопрос 1 Что считается площадью круга? Площадью круга считают число, к которому приближаются площади вписанных правильных многоугольников при увеличении числа их сторон.

Вопрос 2 Чему равна площадь круга радиуса R? Площадь круга равна половине произведения длины его окружности на радиус.

Вопрос 3 Какая фигура называется круговым сектором? Круговым сектором называется общая часть круга и центрального угла с вершиной в центре этого круга.

Вопрос 4 Чему равна площадь кругового сектора?

Вопрос 5 Какая фигура называется круговым сегментом? Круговым сегментом называется часть круга, отсекаемая от него какой-нибудь хордой.

Вопрос 6 Как вычисляется площадь сегмента?

Упражнение 1 Найдите площадь круга, изображенного на рисунке. Стороны квадратных клеток равны 1. Ответ: 8π.

Упражнение 2 Вычислите площадь круга, диаметр которого равен: а) 4 см; б) 10 м. Ответ: а) 4π см2; б) 25π м2.

Упражнение 3 Найдите площадь круга, длина окружности которого равна 1 м.

Упражнение 4 Вычислите радиус круга, площадь которого равна: а) 4 см2; б) 16 м2.

Упражнение 5 Во сколько раз увеличится площадь круга, если его радиус увеличить: а) в 2 раза; б) в 3 раза? Ответ: а) в 4 раза; б) в 9 раз.

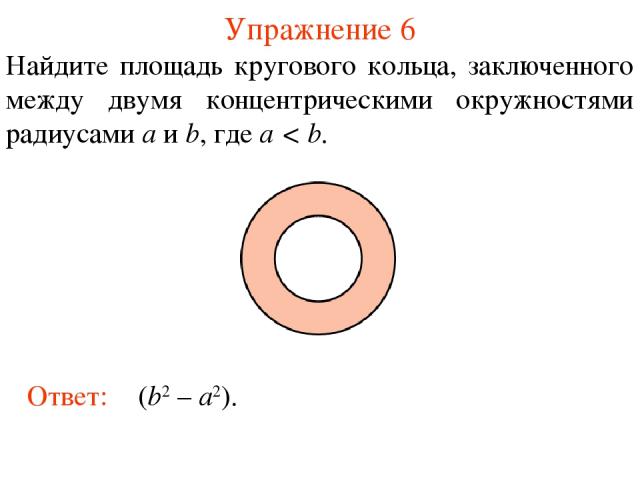
Упражнение 6 Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями радиусами a и b, где a < b. Ответ: π(b2 – a2).

Упражнение 7 Найдите площадь кругового кольца, изображенного на рисунке. Стороны квадратных клеток равны 1. Ответ: 8π.

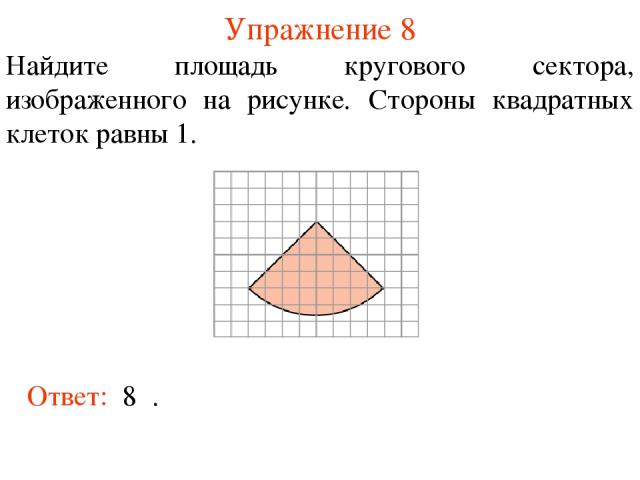
Упражнение 8 Найдите площадь кругового сектора, изображенного на рисунке. Стороны квадратных клеток равны 1. Ответ: 8π.

Упражнение 9 Найдите площадь круга, описанного около прямоугольника со сторонами а и b.

Упражнение 10 Найдите площадь круга, вписанного в равносторонний треугольник со стороной а.

Упражнение 11 Во сколько раз площадь круга, описанного около квадрата, больше площади круга, вписанного в этот квадрат? Ответ: В два раза.

Упражнение 12 Найдите радиус окружности, которая делит круг радиуса R на две равновеликие части - кольцо и круг.

Упражнение 13 На клетчатой бумаге нарисуйте круг с центром в точке O, площадь которого в два раза меньше площади круга, изображенного на рисунке.

Упражнение 14 Найдите площадь сектора круга радиуса R, если соответствующий этому сектору центральный угол равен: а) 60°; б) 40°; в) 150°.

Упражнение 15 Найдите площадь сектора круга радиуса 3, длина дуги которого равна 4. Ответ: 6.

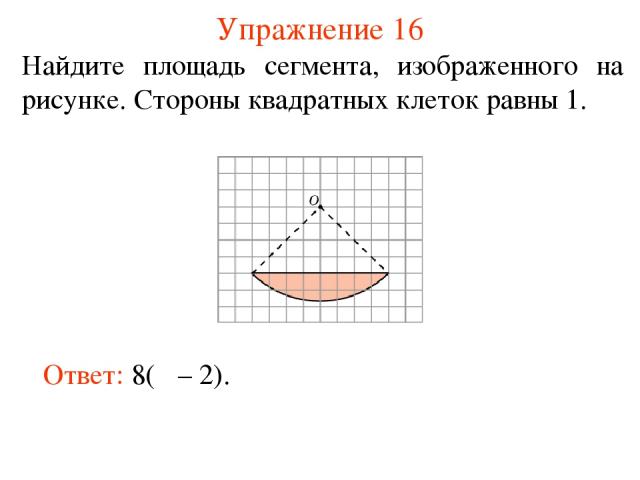
Упражнение 16 Найдите площадь сегмента, изображенного на рисунке. Стороны квадратных клеток равны 1. Ответ: 8(π – 2).

Упражнение 17 Найдите площадь части круга, расположенной вне вписанного в этот круг: а) квадрата; б) правильного треугольника; в) правильного шестиугольника. Радиус круга равен R.

Упражнение 18 Найдите площади заштрихованных фигур.

Упражнение 19 Около правильного многоугольника со стороной а описана окружность, в многоугольник вписана другая окружность. Найдите площадь образовавшегося кольца.

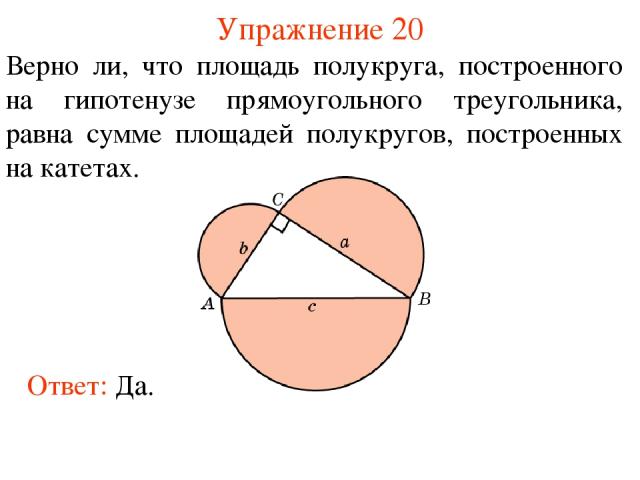
Упражнение 20 Верно ли, что площадь полукруга, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей полукругов, построенных на катетах. Ответ: Да.

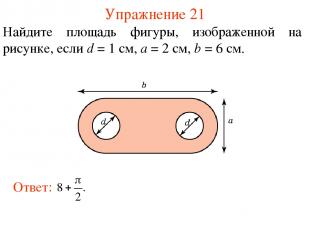
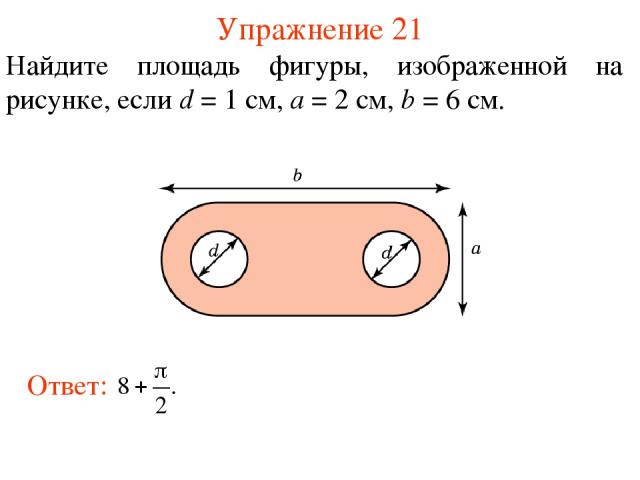
Упражнение 21 Найдите площадь фигуры, изображенной на рисунке, если d = 1 см, а = 2 см, b = 6 см.

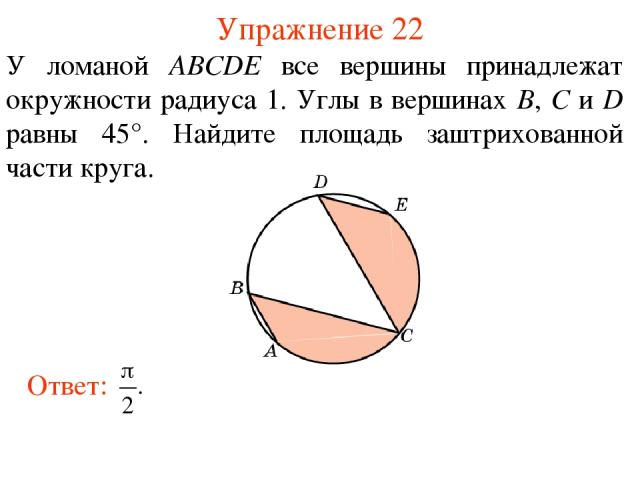
Упражнение 22 У ломаной АВСDE все вершины принадлежат окружности радиуса 1. Углы в вершинах В, С и D равны 45°. Найдите площадь заштрихованной части круга.

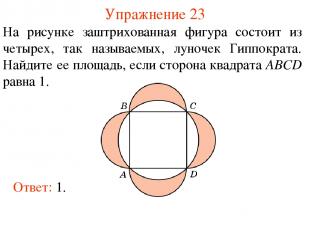
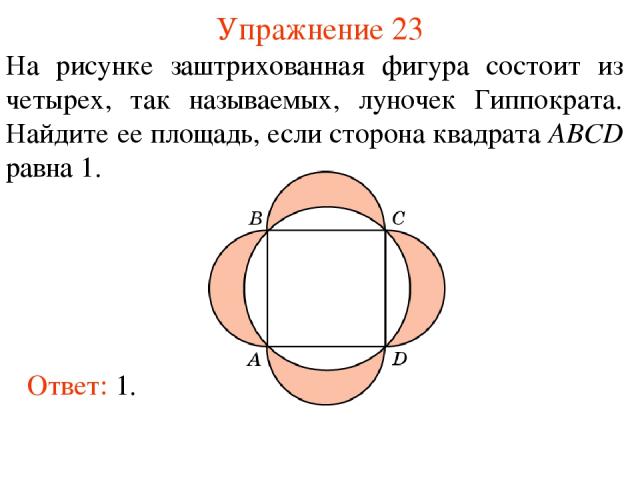
Упражнение 23 На рисунке заштрихованная фигура состоит из четырех, так называемых, луночек Гиппократа. Найдите ее площадь, если сторона квадрата ABCD равна 1. Ответ: 1.

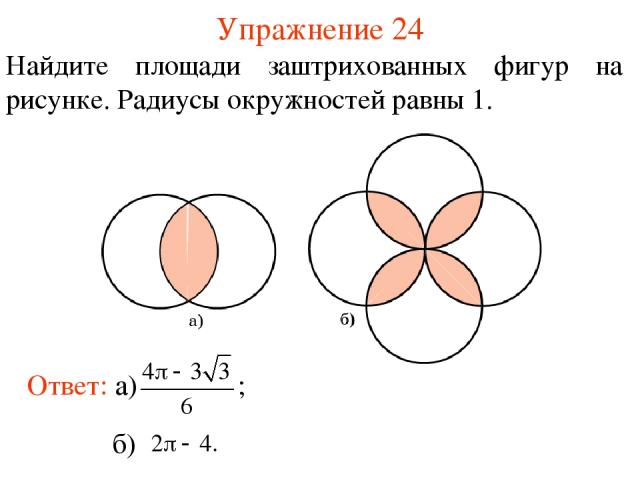
Упражнение 24 Найдите площади заштрихованных фигур на рисунке. Радиусы окружностей равны 1.