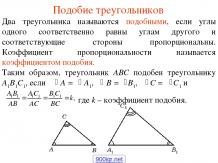
Презентация на тему: Задачи по вписанной и описанной окружности

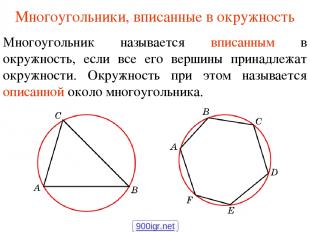
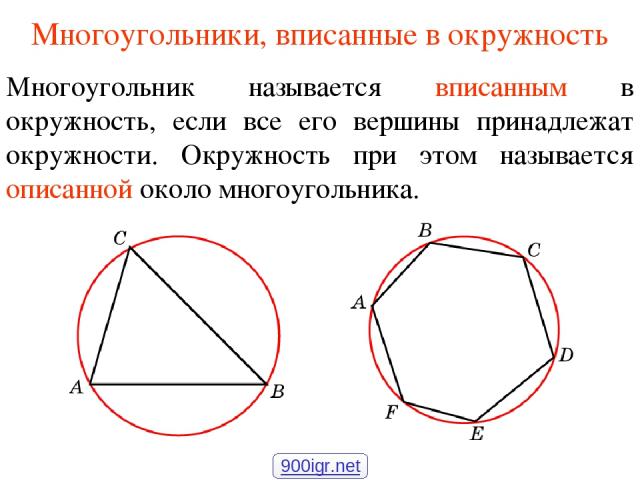
Многоугольники, вписанные в окружность Многоугольник называется вписанным в окружность, если все его вершины принадлежат окружности. Окружность при этом называется описанной около многоугольника. 900igr.net

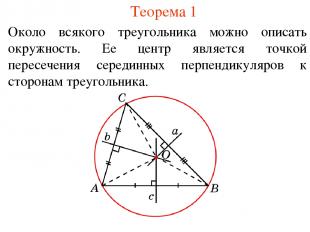
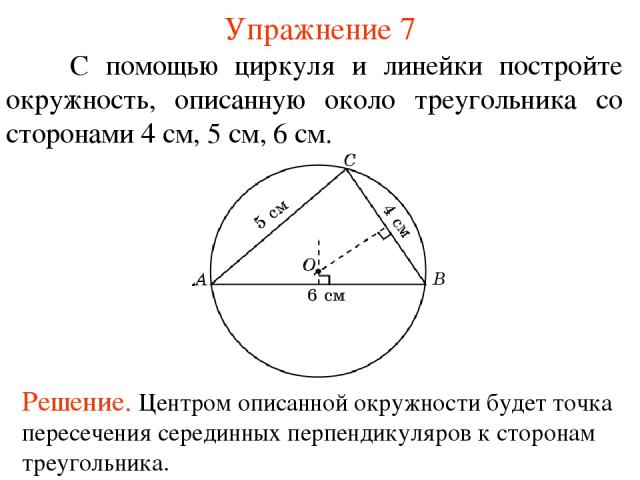
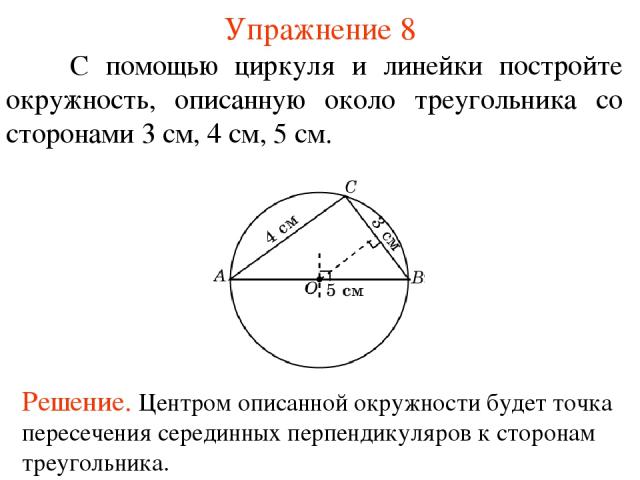
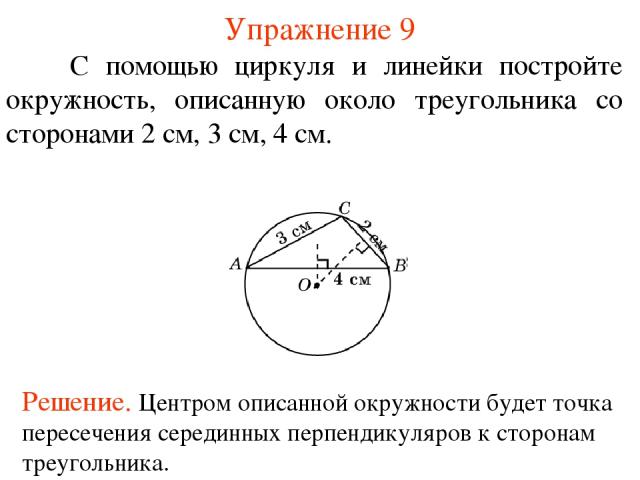
Теорема 1 Около всякого треугольника можно описать окружность. Ее центр является точкой пересечения серединных перпендикуляров к сторонам треугольника.

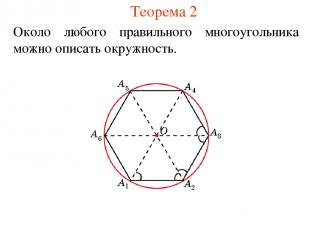
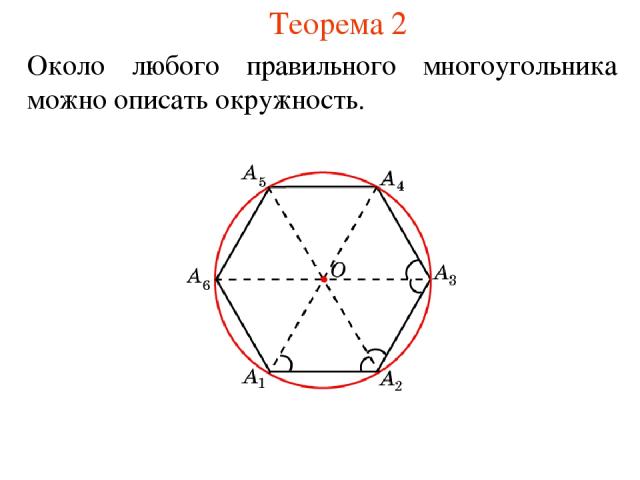
Теорема 2 Около любого правильного многоугольника можно описать окружность.

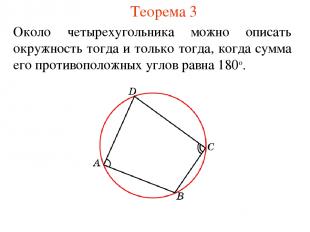
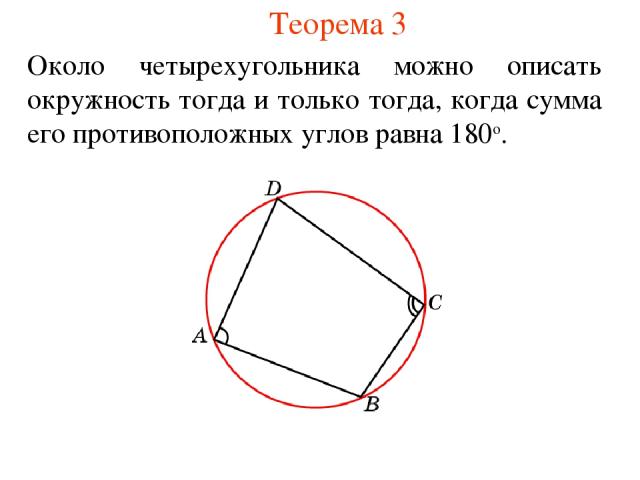
Теорема 3 Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180о.

Вопрос 1 Какой многоугольник называется вписанным в окружность? Ответ: Многоугольник называется вписанным в окружность, если все его вершины принадлежат окружности.

Вопрос 2 Какая окружность называется описанной около многоугольника? Ответ: Окружность называется описанной около многоугольника, если ей принадлежат все вершины этого многоугольника.

Вопрос 3 Около всякого ли треугольника можно описать окружность? Ответ: Да.

Вопрос 4 Где находится центр описанной около треугольника окружности? Ответ: Центром описанной окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.

Вопрос 5 Можно ли описать окружность около правильного многоугольника? Ответ: Да.

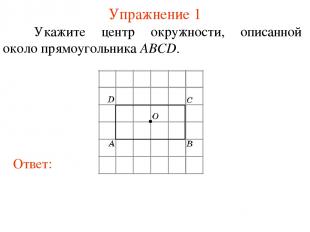
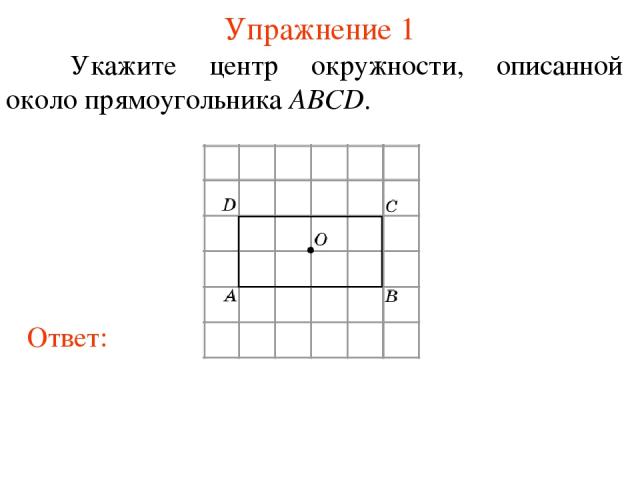
Упражнение 1 Укажите центр окружности, описанной около прямоугольника ABCD.

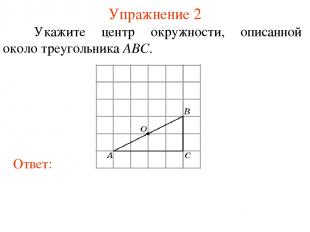
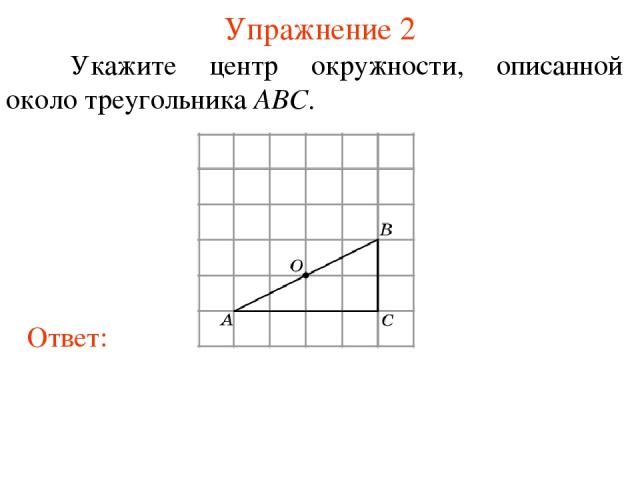
Упражнение 2 Укажите центр окружности, описанной около треугольника ABC.

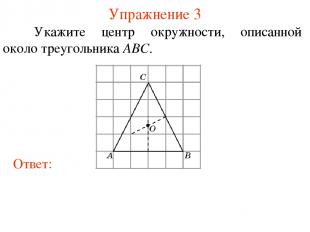
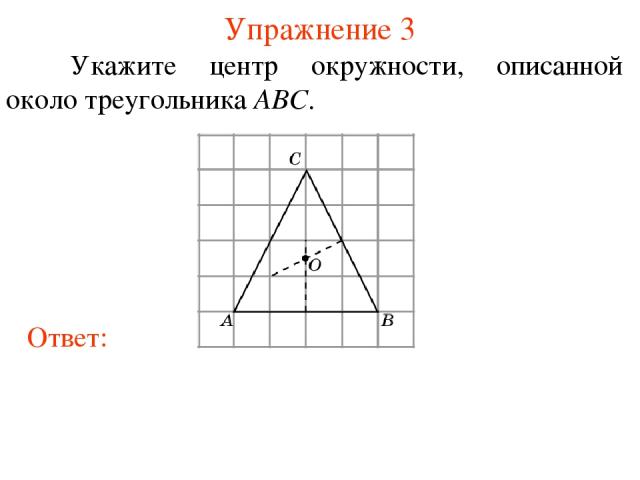
Упражнение 3 Укажите центр окружности, описанной около треугольника ABC.

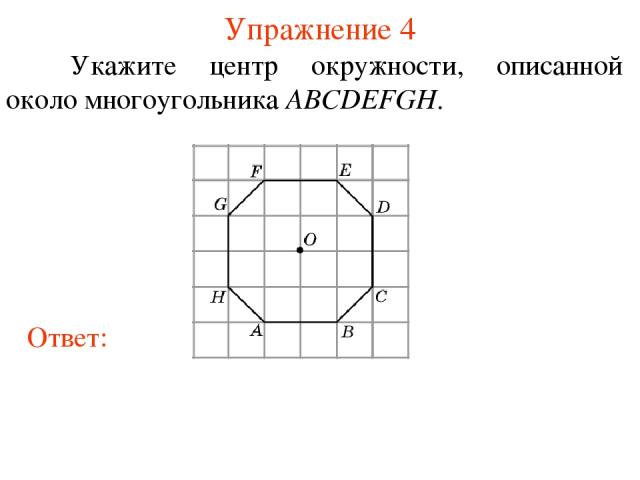
Упражнение 4 Укажите центр окружности, описанной около многоугольника ABCDEFGH.

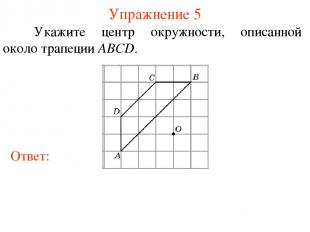
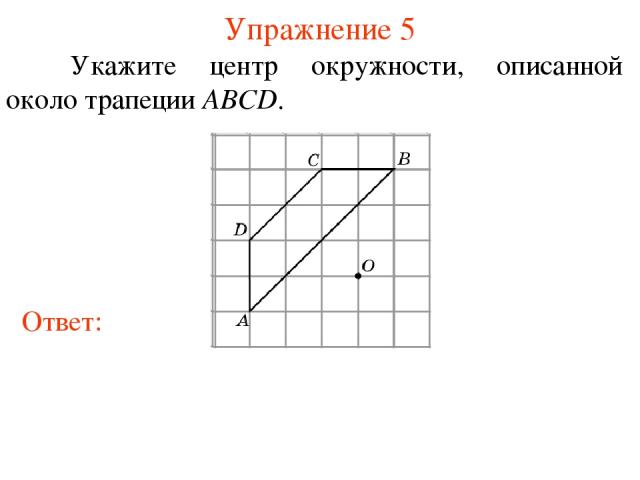
Упражнение 5 Укажите центр окружности, описанной около трапеции ABCD.

Упражнение 6 Может ли центр описанной около треугольника окружности находиться: а) внутри треугольника; б) на стороне треугольника; в) вне этого треугольника? Ответ: а) Да; б) да; в) да.

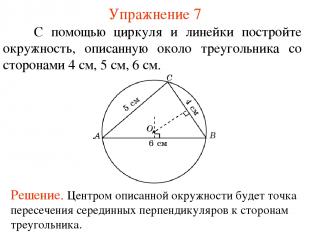
Упражнение 7 С помощью циркуля и линейки постройте окружность, описанную около треугольника со сторонами 4 см, 5 см, 6 см.

Упражнение 8 С помощью циркуля и линейки постройте окружность, описанную около треугольника со сторонами 3 см, 4 см, 5 см.

Упражнение 9 С помощью циркуля и линейки постройте окружность, описанную около треугольника со сторонами 2 см, 3 см, 4 см.

Упражнение 10 Постройте треугольник ABC по двум данным сторонам AB = c, AC = b и радиусу R описанной окружности.

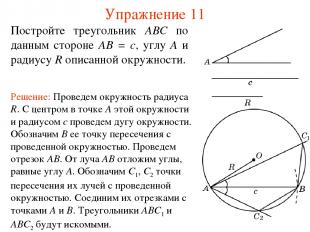
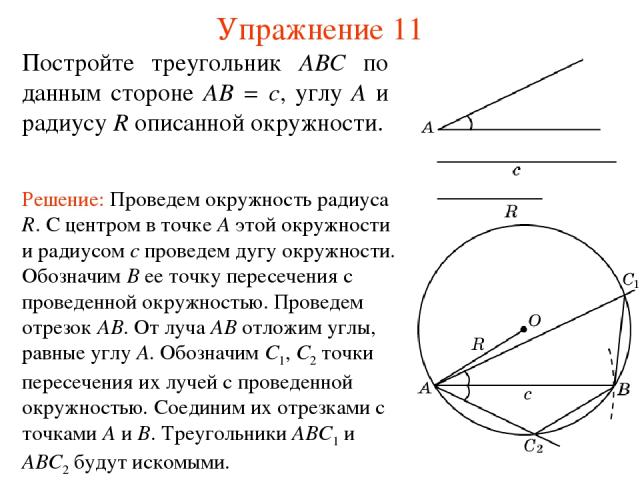
Упражнение 11 Постройте треугольник ABC по данным стороне AB = c, углу A и радиусу R описанной окружности.

Упражнение 12 Всегда ли можно ли описать окружность около: а) прямоугольника; б) параллелограмма; в) ромба; г) квадрата; д) равнобедренной трапеции; е) прямоугольной трапеции? Ответ: а) Да; б) нет; в) нет; г) да; д) да; е) нет.

Упражнение 13 Можно ли описать окружность около четырехугольника, углы которого последовательно равны: а) 70о, 130о, 110о, 50о; б) 90о, 90о, 60о, 120о; в) 45о, 75о, 135о, 105о; г) 40о, 125о, 55о, 140о? Ответ: а) Да; б) нет; в) да; г) нет.

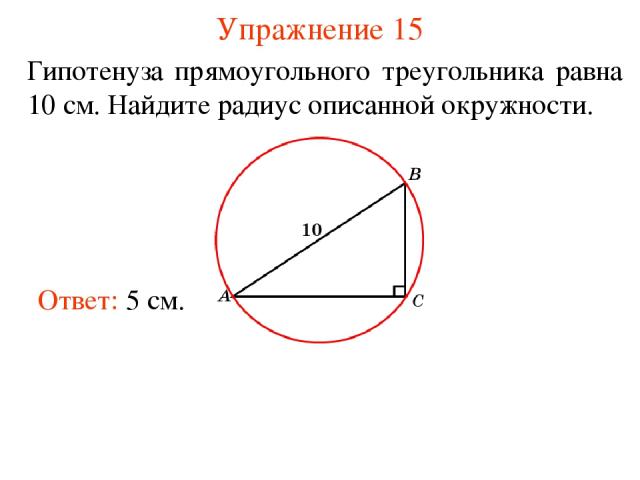
Упражнение 14 Где находится центр окружности, описанной около прямоугольного треугольника? Ответ: В середине гипотенузы.

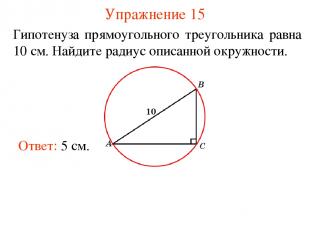
Упражнение 15 Гипотенуза прямоугольного треугольника равна 10 см. Найдите радиус описанной окружности. Ответ: 5 см.

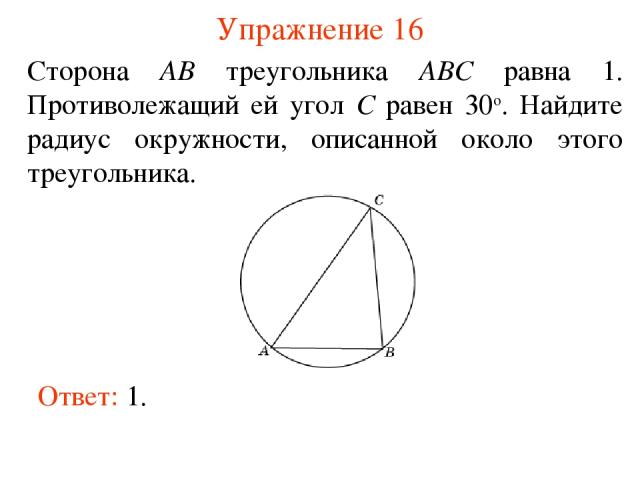
Упражнение 16 Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 30о. Найдите радиус окружности, описанной около этого треугольника. Ответ: 1.

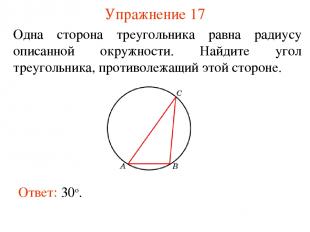
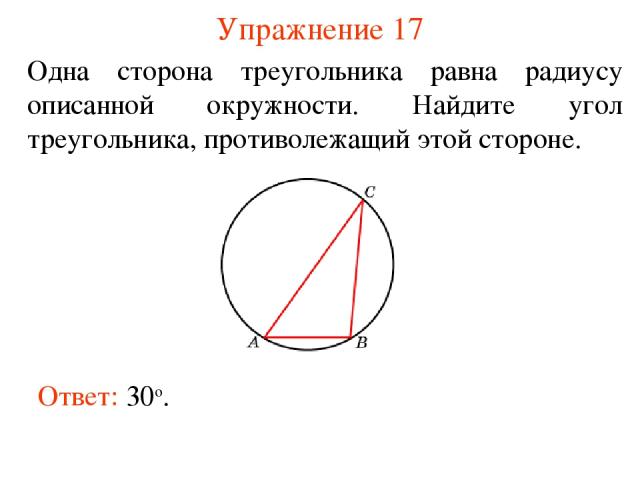
Упражнение 17 Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ: 30о.

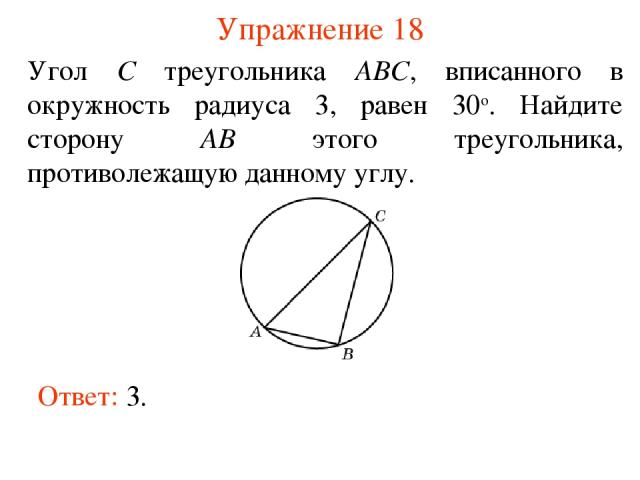
Упражнение 18 Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 30о. Найдите сторону AB этого треугольника, противолежащую данному углу. Ответ: 3.

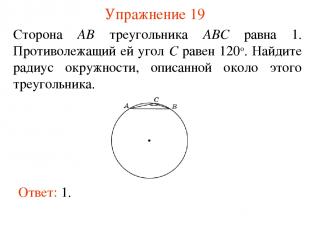
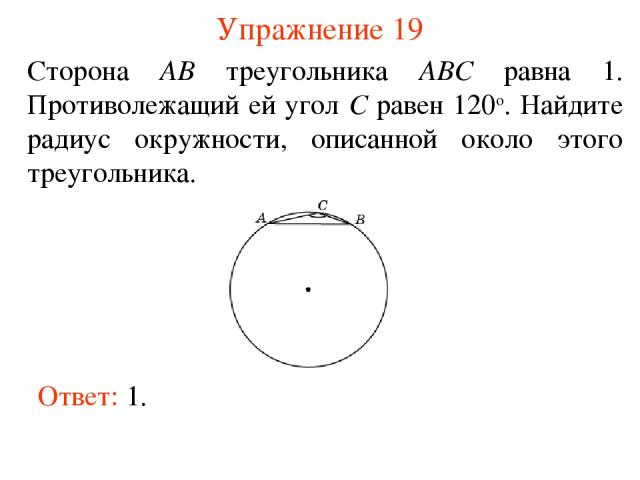
Упражнение 19 Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 120о. Найдите радиус окружности, описанной около этого треугольника. Ответ: 1.

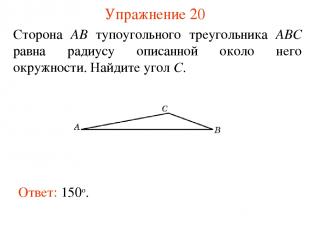
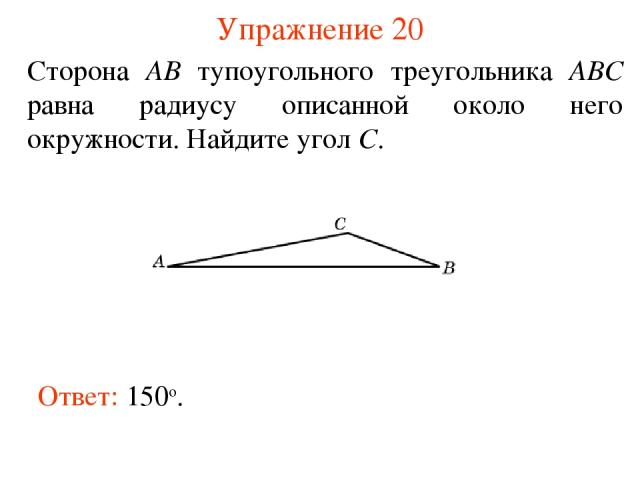
Упражнение 20 Сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ: 150о.

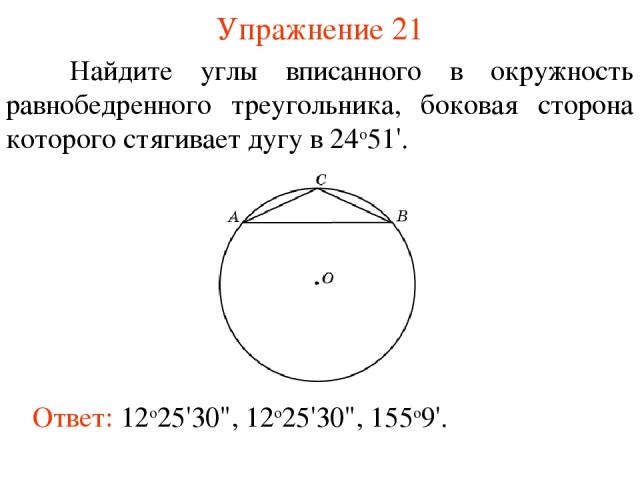
Упражнение 21 Ответ: 12о25'30", 12о25'30", 155о9'. Найдите углы вписанного в окружность равнобедренного треугольника, боковая сторона которого стягивает дугу в 24о51'.

Упражнение 22 Найдите углы вписанного в окружность равнобедренного треугольника, если его основание стягивает дугу в 100о.

Упражнение 23 Два угла треугольника равны 60о и 40о. Под какими углами видны его стороны из центра описанной около него окружности? Ответ: 120о, 80о и 160о.

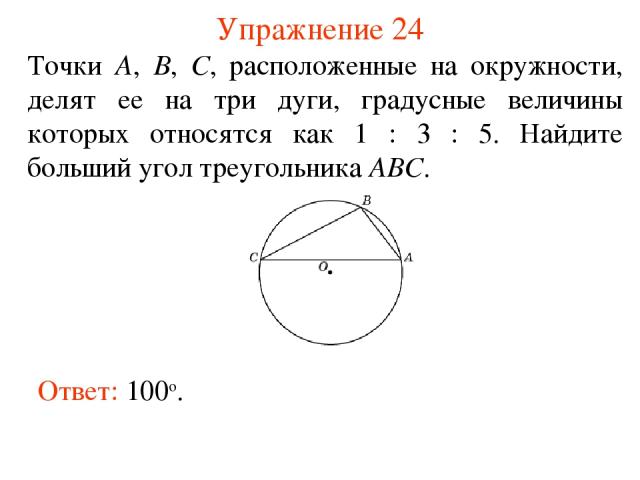
Упражнение 24 Ответ: 100о. Точки А, В, С, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1 : 3 : 5. Найдите больший угол треугольника АВС.

Упражнение 25 Ответ: 30о, 45о и 105о. Точки А, В, С, расположенные на окружности, делят эту окружность на три дуги, градусные величины которых относятся как 2 : 3 : 7. Найдите углы треугольника АВС.

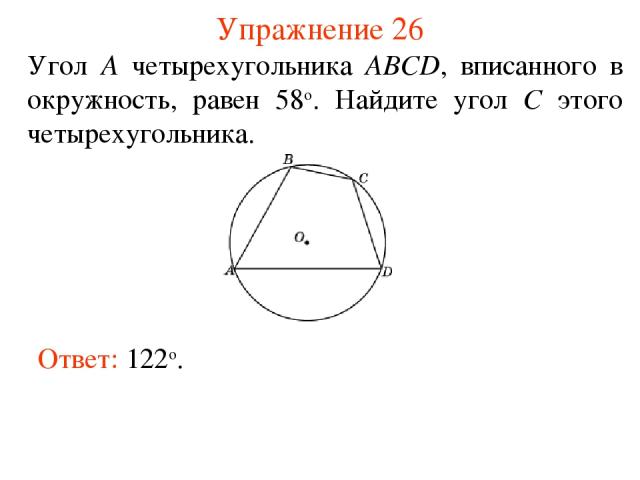
Упражнение 26 Ответ: 122о. Угол A четырехугольника ABCD, вписанного в окружность, равен 58о. Найдите угол С этого четырехугольника.

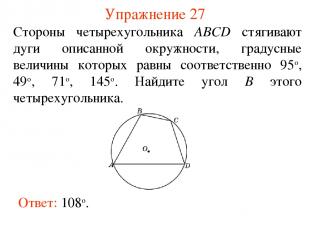
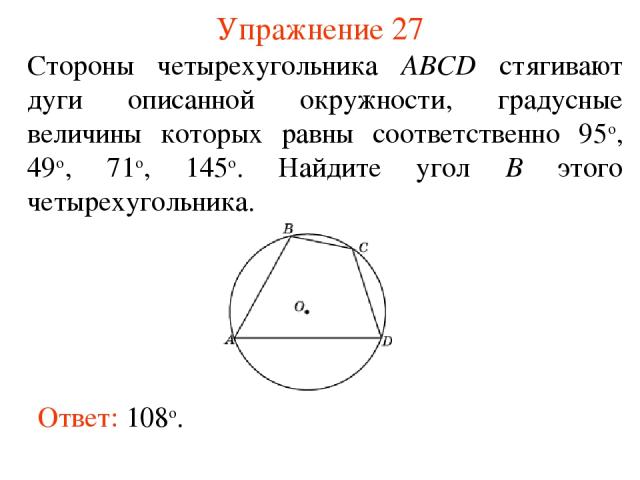
Упражнение 27 Ответ: 108о. Стороны четырехугольника ABCD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95о, 49о, 71о, 145о. Найдите угол B этого четырехугольника.

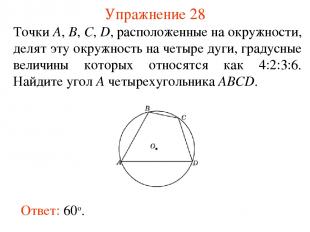
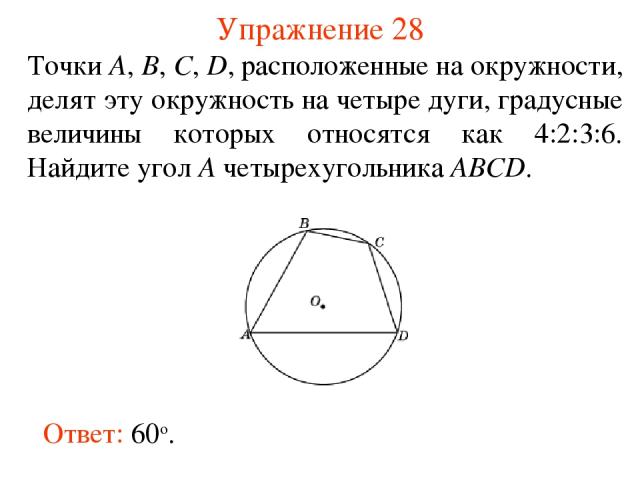
Упражнение 28 Точки А, В, С, D, расположенные на окружности, делят эту окружность на четыре дуги, градусные величины которых относятся как 4:2:3:6. Найдите угол A четырехугольника АВСD. Ответ: 60о.

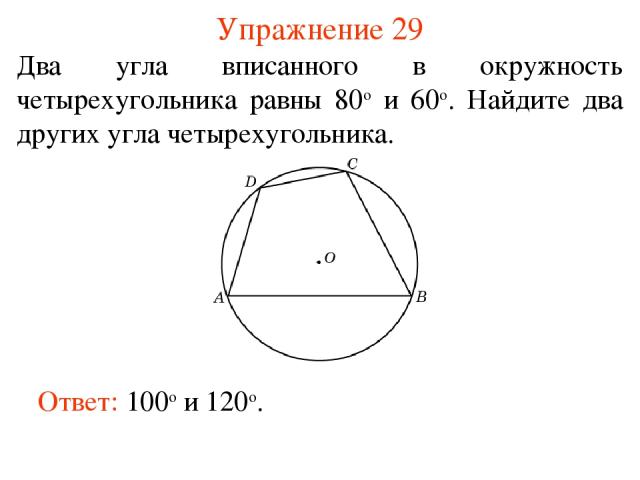
Упражнение 29 Два угла вписанного в окружность четырехугольника равны 80о и 60о. Найдите два других угла четырехугольника. Ответ: 100о и 120о.

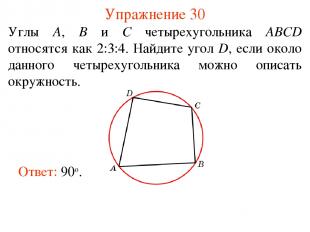
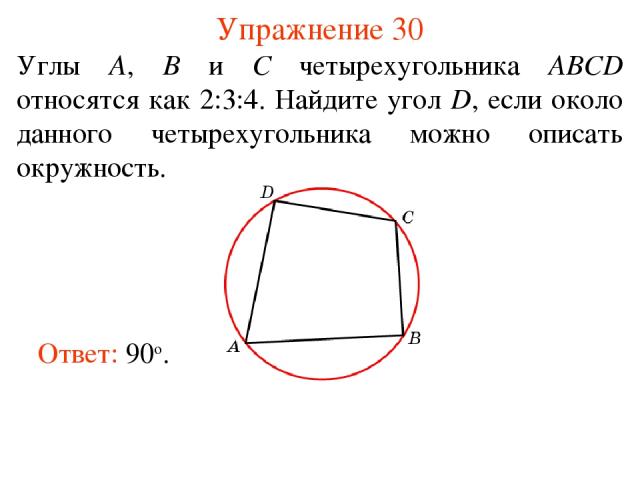
Упражнение 30 Углы A, B и C четырехугольника ABCD относятся как 2:3:4. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ: 90о.

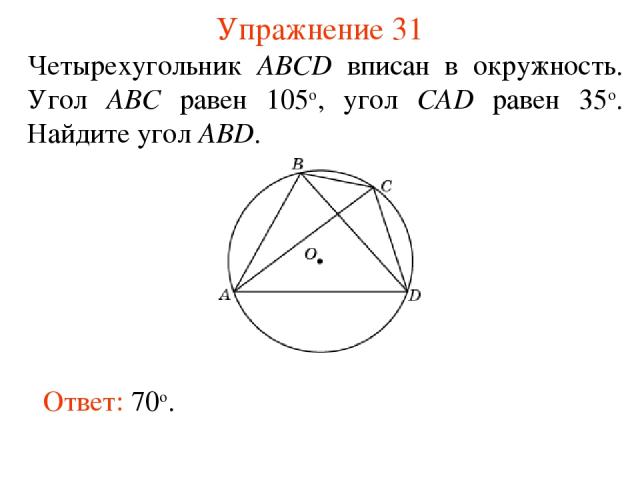
Упражнение 31 Четырехугольник ABCD вписан в окружность. Угол ABC равен 105о, угол CAD равен 35о. Найдите угол ABD. Ответ: 70о.

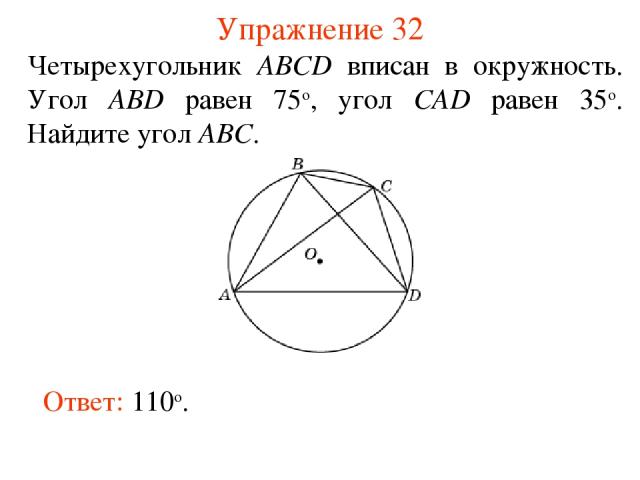
Упражнение 32 Четырехугольник ABCD вписан в окружность. Угол ABD равен 75о, угол CAD равен 35о. Найдите угол ABC. Ответ: 110о.

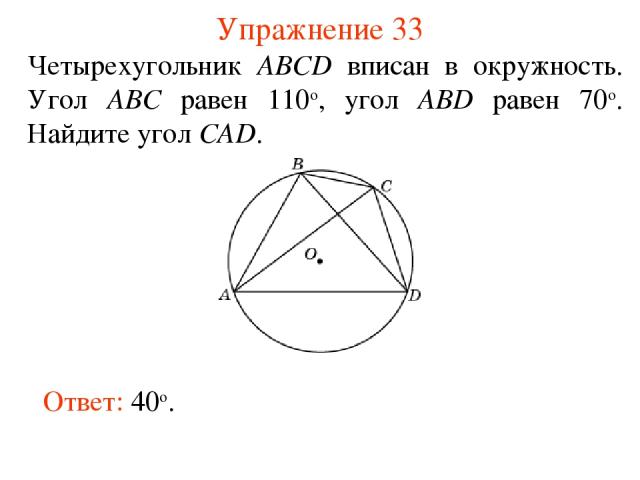
Упражнение 33 Четырехугольник ABCD вписан в окружность. Угол ABC равен 110о, угол ABD равен 70о. Найдите угол CAD. Ответ: 40о.

Упражнение 34 Ответ: Против угла в 30о. Углы треугольника равны 30о, 65о и 85о. Какая из сторон треугольника расположена дальше от центра описанной окружности?

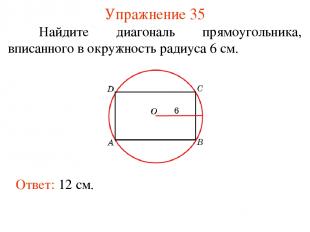
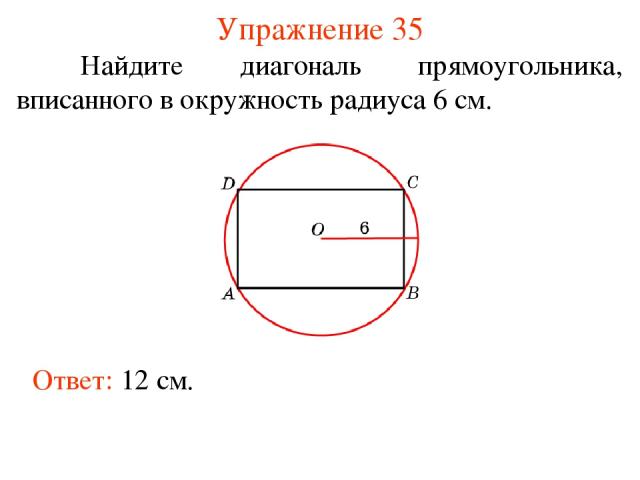
Упражнение 35 Найдите диагональ прямоугольника, вписанного в окружность радиуса 6 см. Ответ: 12 см.

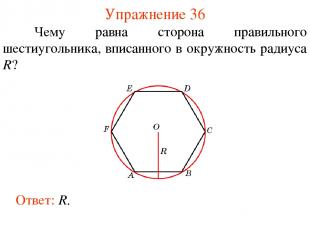
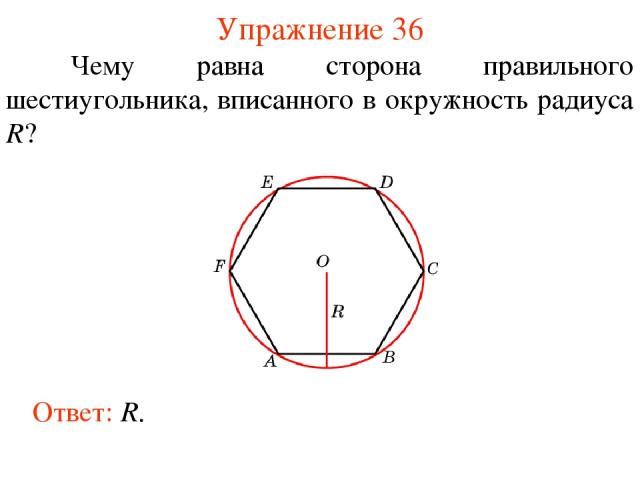
Упражнение 36 Ответ: R. Чему равна сторона правильного шестиугольника, вписанного в окружность радиуса R?

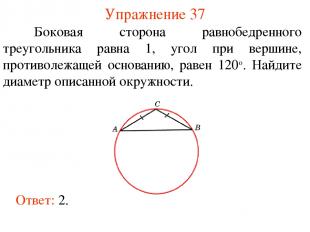
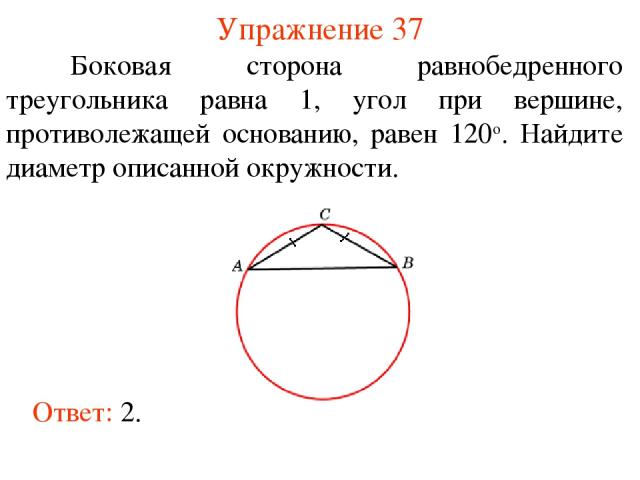
Упражнение 37 Ответ: 2. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120о. Найдите диаметр описанной окружности.

Упражнение 38 Меньшая сторона прямоугольника равна 5 см. Угол между диагоналями равен 60о. Найдите радиус описанной окружности. Ответ: 5 см.

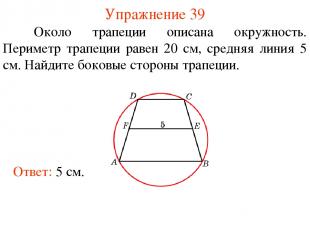
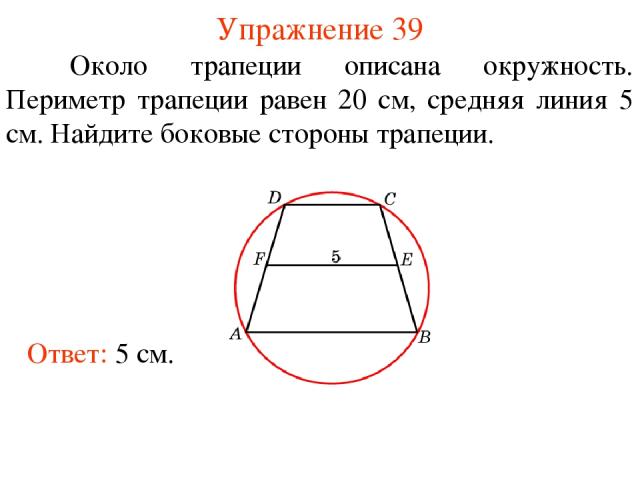
Упражнение 39 Около трапеции описана окружность. Периметр трапеции равен 20 см, средняя линия 5 см. Найдите боковые стороны трапеции. Ответ: 5 см.

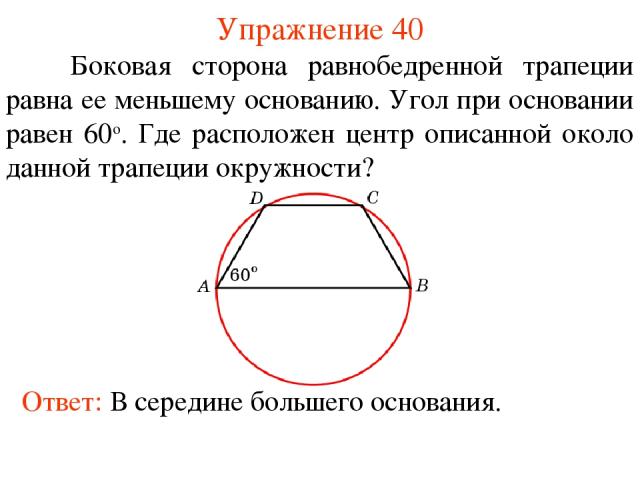
Упражнение 40 Боковая сторона равнобедренной трапеции равна ее меньшему основанию. Угол при основании равен 60о. Где расположен центр описанной около данной трапеции окружности? Ответ: В середине большего основания.

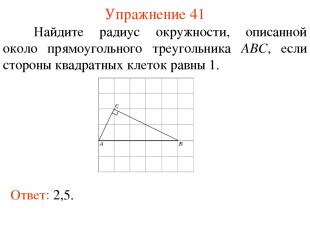
Упражнение 41 Найдите радиус окружности, описанной около прямоугольного треугольника ABC, если стороны квадратных клеток равны 1. Ответ: 2,5.

Упражнение 42 Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны квадратных клеток равны 1. Ответ: 2,5.

Упражнение 43* Можно ли описать окружность около пятиугольника с углами 80о, 90о, 100о, 130о, 140о? Из этого вытекает, что сумма любых двух несоседних углов любого вписанного пятиугольника больше 180о. Указанные в задаче углы не удовлетворяют этому условию, и, значит, около такого пятиугольника нельзя описать окружность.

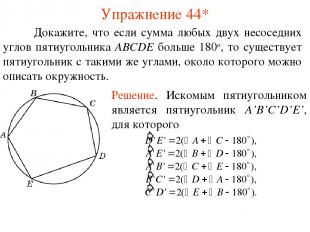
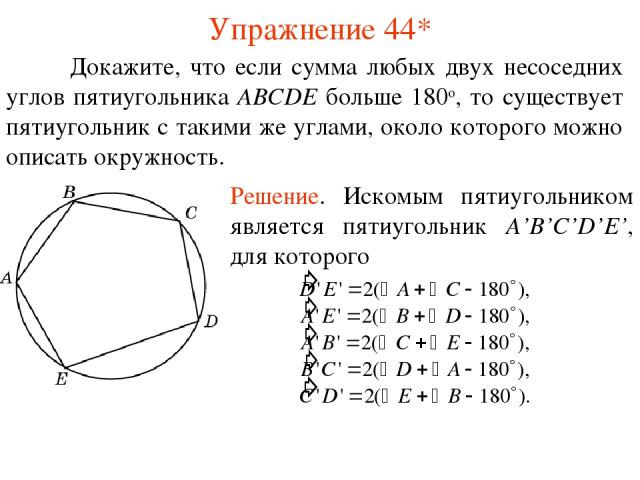
Упражнение 44* Докажите, что если сумма любых двух несоседних углов пятиугольника ABCDE больше 180о, то существует пятиугольник с такими же углами, около которого можно описать окружность.

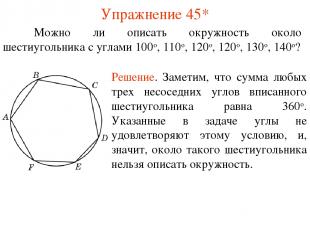
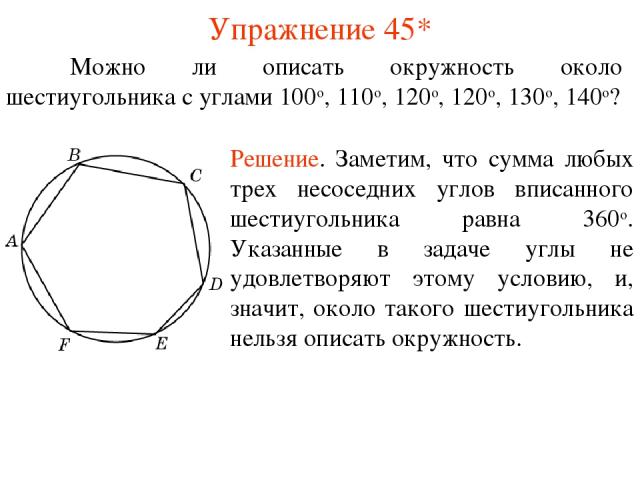
Упражнение 45* Можно ли описать окружность около шестиугольника с углами 100о, 110о, 120о, 120о, 130о, 140о? Решение. Заметим, что сумма любых трех несоседних углов вписанного шестиугольника равна 360о. Указанные в задаче углы не удовлетворяют этому условию, и, значит, около такого шестиугольника нельзя описать окружность.

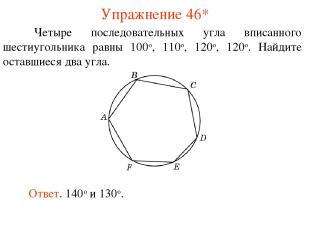
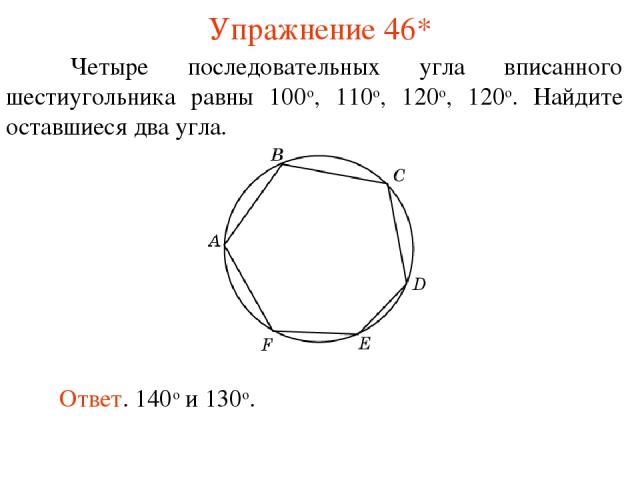
Упражнение 46* Четыре последовательных угла вписанного шестиугольника равны 100о, 110о, 120о, 120о. Найдите оставшиеся два угла. Ответ. 140о и 130о.

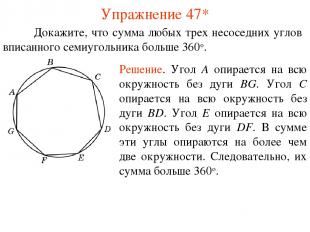
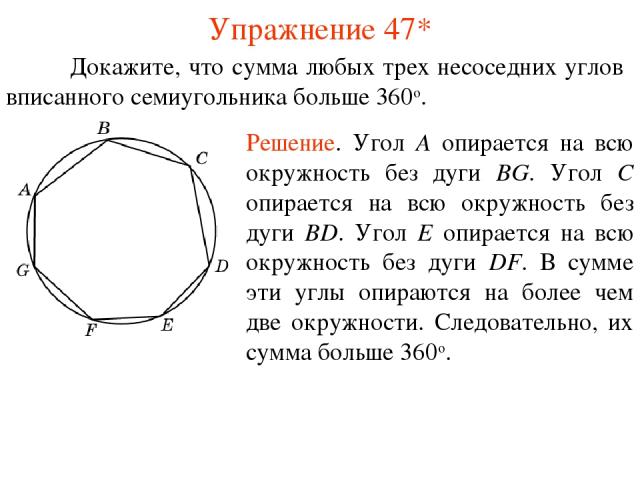
Упражнение 47* Докажите, что сумма любых трех несоседних углов вписанного семиугольника больше 360о. Решение. Угол A опирается на всю окружность без дуги BG. Угол C опирается на всю окружность без дуги BD. Угол E опирается на всю окружность без дуги DF. В сумме эти углы опираются на более чем две окружности. Следовательно, их сумма больше 360о.