Презентация на тему: Координатный метод в пространстве

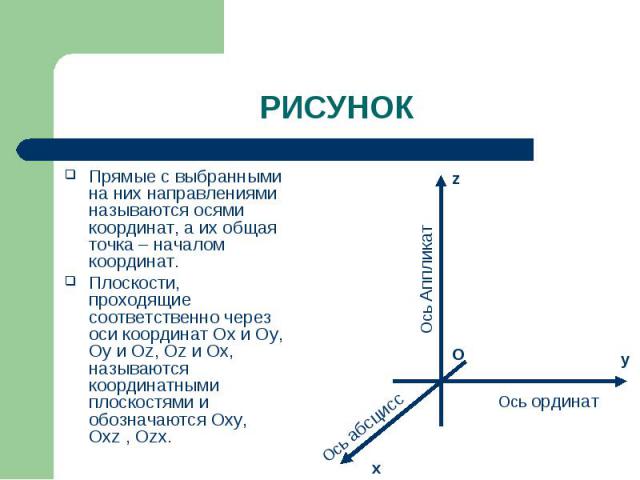
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждом из них выбрано направление(оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве. Если через точку пространства проведены три попарно перпендикулярные прямые, на каждом из них выбрано направление(оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве. Рассмотрим рисунок

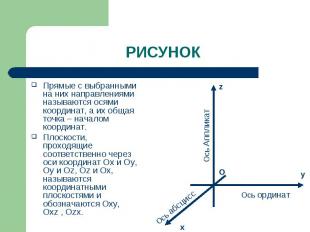
Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат. Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат. Плоскости, проходящие соответственно через оси координат Ох и Оy, Oу и Оz, Oz и Ox, называются координатными плоскостями и обозначаются Oxy, Oхz , Ozх.

Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч – отрицательной полуосью. Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч – отрицательной полуосью.

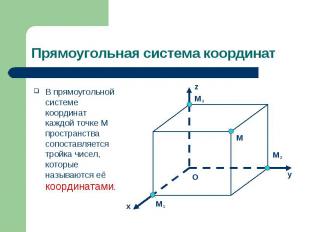
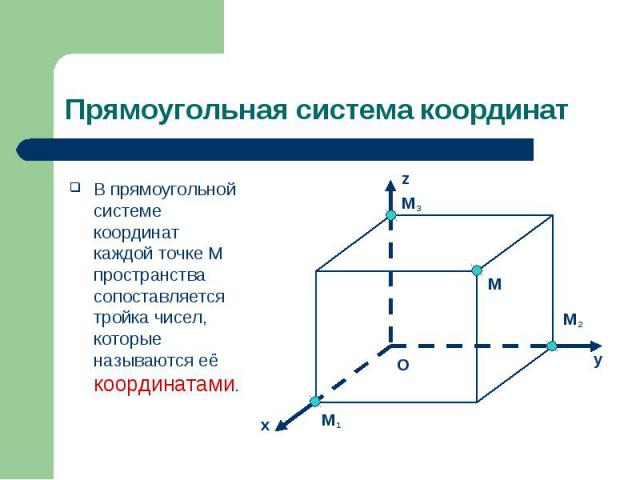
В прямоугольной системе координат каждой точке M пространства сопоставляется тройка чисел, которые называются её координатами. В прямоугольной системе координат каждой точке M пространства сопоставляется тройка чисел, которые называются её координатами.

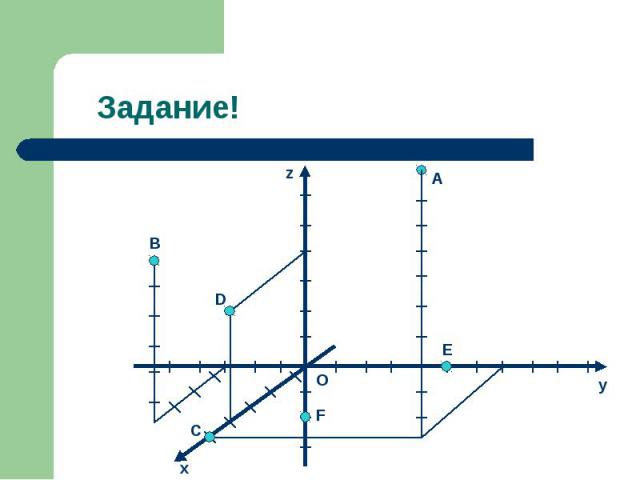
Если, например, точка M лежит на координатной плоскости или на оси координат, то некоторые её координаты равны нулю. Так, если M принадлежит Oxy, то аппликата точка M равна нулю: z=0. Аналогично если M принадлежит Oхz, то y=0, а если M принадлежит Oyz, то x=0. Если M принадлежит Ox, то ордината и аппликата точки M равна нулю: y=0 и z=0. Если M принадлежит Oy, то x=0 и z=0; если M принадлежит Oz, то x=0 и y=0. Все три координаты начала координат равны нулю: О (0;0;0). Напиши координаты для точек A, B, C, D, E, F на рисунке следующего слайда. Если, например, точка M лежит на координатной плоскости или на оси координат, то некоторые её координаты равны нулю. Так, если M принадлежит Oxy, то аппликата точка M равна нулю: z=0. Аналогично если M принадлежит Oхz, то y=0, а если M принадлежит Oyz, то x=0. Если M принадлежит Ox, то ордината и аппликата точки M равна нулю: y=0 и z=0. Если M принадлежит Oy, то x=0 и z=0; если M принадлежит Oz, то x=0 и y=0. Все три координаты начала координат равны нулю: О (0;0;0). Напиши координаты для точек A, B, C, D, E, F на рисунке следующего слайда.

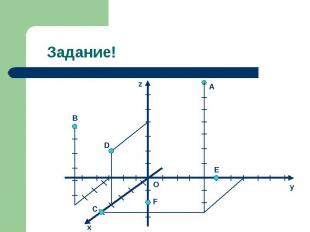
A(5; 4; 10), A(5; 4; 10), B(4; -3; 6), C(5; 0; 0), D(4; 0; 4), E(0; 5; 0), F(0; 0; -2). Сравни свои ответы.

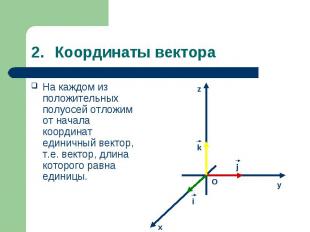
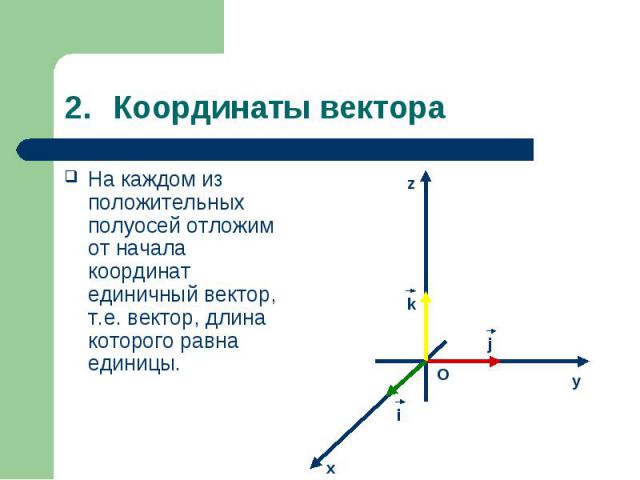
На каждом из положительных полуосей отложим от начала координат единичный вектор, т.е. вектор, длина которого равна единицы. На каждом из положительных полуосей отложим от начала координат единичный вектор, т.е. вектор, длина которого равна единицы.

Любой вектор a можно разложить по координатным векторам, т.е. представить в виде Любой вектор a можно разложить по координатным векторам, т.е. представить в виде а = xi + yj + zk Причем коэффициенты разложения x, y, z определяются единственным образом.

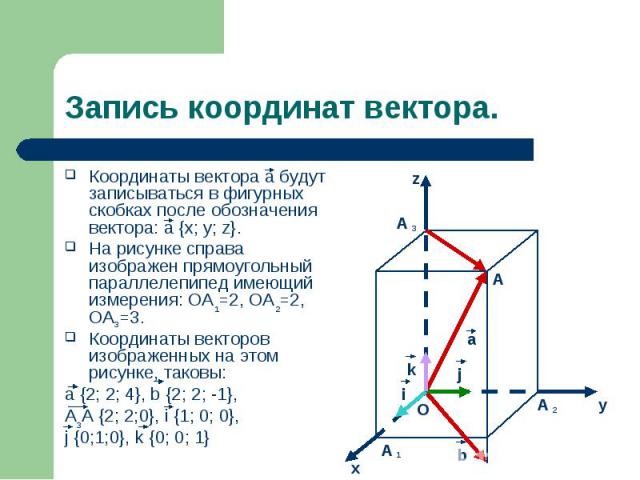
Координаты вектора а будут записываться в фигурных скобках после обозначения вектора: а {x; y; z}. Координаты вектора а будут записываться в фигурных скобках после обозначения вектора: а {x; y; z}. На рисунке справа изображен прямоугольный параллелепипед имеющий измерения: OA =2, OA =2, OA =3. Координаты векторов изображенных на этом рисунке, таковы: a {2; 2; 4}, b {2; 2; -1}, A A {2; 2;0}, i {1; 0; 0}, j {0;1;0}, k {0; 0; 1}

Так как нулевой вектор можно представить в виде 0 = 0i + 0j + 0k, то все координаты нулевого вектора равны нулю. Так как нулевой вектор можно представить в виде 0 = 0i + 0j + 0k, то все координаты нулевого вектора равны нулю. Координаты равных векторов соответственно равны, т.е. если векторы a {x ; y ; z } и b {x ; y ; z } равны, то x =x , y =y и z =z .

Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Если a {x ; y ; z } и b {x ; y ; z } – данные векторы, то вектор a + b имеет координаты Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Если a {x ; y ; z } и b {x ; y ; z } – данные векторы, то вектор a + b имеет координаты {x +x ; y +y ; z +z }

Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Если a {x ; y ; z } и b {x ; y ; z } – данные векторы, то вектор a – b имеет координаты Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Если a {x ; y ; z } и b {x ; y ; z } – данные векторы, то вектор a – b имеет координаты {x –x ; y –y ; z –z }

Каждая координата произведения вектора на число равна произведение соответствующей координаты вектора на это число. Если a {x; y; z } – данный вектор, α - данное число, то вектор αa имеет координаты Каждая координата произведения вектора на число равна произведение соответствующей координаты вектора на это число. Если a {x; y; z } – данный вектор, α - данное число, то вектор αa имеет координаты { x; y; z}

Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус-вектором данной точки. Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус-вектором данной точки. Координаты любой точки равны соответствующим координатам её радиус-вектора. Каждая координата вектора равна разности соответствующих координат его конца и начала.

Каждая координата середины отрезка равна полусумме соответствующих координат его концов. Каждая координата середины отрезка равна полусумме соответствующих координат его концов. Длина вектора a {x; y; z} вычисляется по формуле |a| = √x² + y² + z²

Расстояния между точка M (x ; y ; z ) и Расстояния между точка M (x ; y ; z ) и M (x ; y ; z ) вычисляется по формуле d = √(x – x )² + (y – y )² + (z – z )²

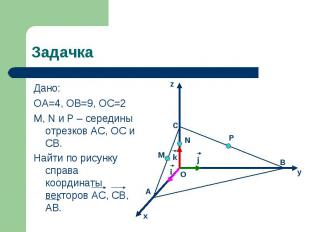
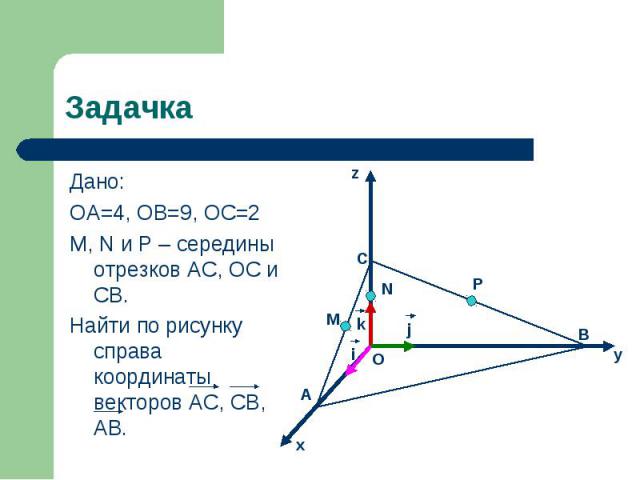
Дано: Дано: ОА=4, ОВ=9, ОС=2 M, N и P – середины отрезков AC, OC и CB. Найти по рисунку справа координаты векторов AC, CB, AB.

AC = AO + OC = 4i + 2k, AC {-4; 0; 2} AC = AO + OC = 4i + 2k, AC {-4; 0; 2} CB = CO + OB = 2k + 9j, CB {0; 9; 2} AB = AO + OB = -4i + 9j, AB {-4; 7; 0}

Презентация сделана по учебнику геометрии для 10 -11 класса Презентация сделана по учебнику геометрии для 10 -11 класса Авторы: Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Л. С. Киселёва, Э. Г. Позняк Издание подготовлено под научным руководством академика А. Н. Тихонова. Презентацию делал: Ученик 11 “A” класса, ХСОШ №5, города Хотьково Витушки Сергей Валерьевич. Классный руководитель: Шмелёва Ольга Владимировна.