Презентация на тему: Зачем нужна геометрия

Что означает термин геометрия??? Что означает термин геометрия??? Из истории возникновения геометрии. Где изучают геометрию? Виды углов. Виды треугольников. Зачем нужна геометрия??? А если б не было геометрии??? Источники информации.

ГЕОМЕТРИЯ, раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. ГЕОМЕТРИЯ, раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию.

Одним из наиболее знаменитых учеников Фалеса был Пифагор (ок. 570 — ок. 500 до н.э.). Он много путешествовал, а потом поселился в Кротоне, в Италии, где основал общество, занимавшееся изучением арифметики, музыки, геометрии и астрономии. Пифагор и его последователи доказали много новых теорем о треугольниках, окружностях, пропорциях и некоторых трехмерных телах. Пифагор доказал также знаменитую теорему, носящую ныне его имя, согласно которой площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах. Одним из наиболее знаменитых учеников Фалеса был Пифагор (ок. 570 — ок. 500 до н.э.). Он много путешествовал, а потом поселился в Кротоне, в Италии, где основал общество, занимавшееся изучением арифметики, музыки, геометрии и астрономии. Пифагор и его последователи доказали много новых теорем о треугольниках, окружностях, пропорциях и некоторых трехмерных телах. Пифагор доказал также знаменитую теорему, носящую ныне его имя, согласно которой площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах. Средневековье. После падения Александрии большинство работ древнегреческих математиков были рассеяны или утрачены. Некоторые из них, в том числе Начала Евклида, были переведены и изучались арабами и индийцами. И хотя эти народы породили нескольких великих математиков, среди которых наиболее известны индийские математики Ариабхата (ок. 476 — ок. 550) и Бхаскара II (ок. 1114-1185), все же их самой большой заслугой следует считать сохранение геометрии в период Средневековья.

Новое время. За последние 300 лет доказательная геометрия была существенно расширена, а по своим методам и степени общности результатов она стала заметно отличаться от элементарной геометрии (т.е. геометрии, изложенной в Началах). Французский математик Ж.Дезарг (1593-1662) в связи с развитием учения о перспективе занялся исследованием свойств геометрических фигур в зависимости от их проекций. Тем самым он заложил основу проективной геометрии, которая изучает те свойства фигур, которые остаются неизменными при различных проекциях. В 19 в. это направление получило существенное развитие. Проективная геометрия, конические сечения и новая геометрия треугольников и окружностей составили содержание современной  т. н. чистой геометрии. Новое время. За последние 300 лет доказательная геометрия была существенно расширена, а по своим методам и степени общности результатов она стала заметно отличаться от элементарной геометрии (т.е. геометрии, изложенной в Началах). Французский математик Ж.Дезарг (1593-1662) в связи с развитием учения о перспективе занялся исследованием свойств геометрических фигур в зависимости от их проекций. Тем самым он заложил основу проективной геометрии, которая изучает те свойства фигур, которые остаются неизменными при различных проекциях. В 19 в. это направление получило существенное развитие. Проективная геометрия, конические сечения и новая геометрия треугольников и окружностей составили содержание современной  т. н. чистой геометрии.

по-английски geometry по-английски geometry по-немецки Geometrie по-французски géométrie по-итальянски geometria по-испански geometría

В наше время, геометрия – актуальная наука, изучающаяся во всех школах, университетах и ВУЗах. В наше время, геометрия – актуальная наука, изучающаяся во всех школах, университетах и ВУЗах. В школах дети изучают этот предмет с 7 класса. Геометрия требует к себе придельной внимательности и тщательной подготовке к уроку. Геометрия – важная вещь в жизни каждого человека, так что относиться к ней с важностью стоит с первого знакомства.

А как представить себе жизнь без геометрических фигур??? А как представить себе жизнь без геометрических фигур??? Сейчас я покажу вам их разнообразие. Без них мы не смогли бы жить! Нельзя даже представить такого!!!

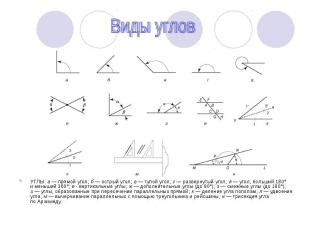
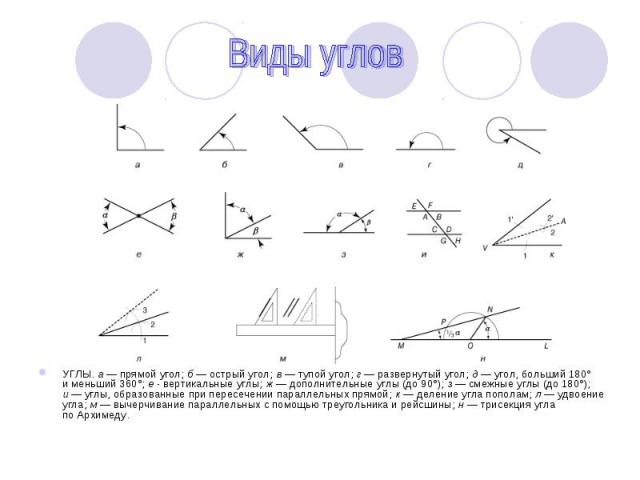
УГЛЫ. а — прямой угол; б — острый угол; в — тупой угол; г — развернутый угол; д — угол, больший 180° и меньший 360°; е - вертикальные углы; ж — дополнительные углы (до 90°); з — смежные углы (до 180°); и — углы, образованные при пересечении параллельных прямой; к — деление угла пополам; л — удвоение угла; м — вычерчивание параллельных с помощью треугольника и рейсшины; н — трисекция угла по Архимеду. УГЛЫ. а — прямой угол; б — острый угол; в — тупой угол; г — развернутый угол; д — угол, больший 180° и меньший 360°; е - вертикальные углы; ж — дополнительные углы (до 90°); з — смежные углы (до 180°); и — углы, образованные при пересечении параллельных прямой; к — деление угла пополам; л — удвоение угла; м — вычерчивание параллельных с помощью треугольника и рейсшины; н — трисекция угла по Архимеду.

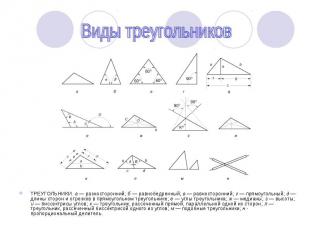
ТРЕУГОЛЬНИКИ. а — разносторонний; б — равнобедренный; в — равносторонний; г — прямоугольный; д — длины сторон и отрезков в прямоугольном треугольнике; е — углы треугольника; ж — медианы; з — высоты; и — биссектрисы углов; к — треугольник, рассеченный прямой, параллельной одной из сторон; л — треугольник, рассеченный биссектрисой одного из углов; м — подобные треугольники; н - пропорциональный делитель. ТРЕУГОЛЬНИКИ. а — разносторонний; б — равнобедренный; в — равносторонний; г — прямоугольный; д — длины сторон и отрезков в прямоугольном треугольнике; е — углы треугольника; ж — медианы; з — высоты; и — биссектрисы углов; к — треугольник, рассеченный прямой, параллельной одной из сторон; л — треугольник, рассеченный биссектрисой одного из углов; м — подобные треугольники; н - пропорциональный делитель.

Правила запоминаются лучше, когда они имеют веселую формулировку. Все знают, что Правила запоминаются лучше, когда они имеют веселую формулировку. Все знают, что «Биссектриса – Это крыса, Которая лазит по углам И делит угол пополам». CС1 – биссектриса угла abc1

Для запоминания так же используется шуточная рифмовка теоремы Пифагора: Для запоминания так же используется шуточная рифмовка теоремы Пифагора: «Пифагоровы штаны во все стороны равны!»

Вопрос: Кто из математиков древности погиб от руки римского солдата, гордо воскликнув: «Отойди, не трогай моих чертежей!» Вопрос: Кто из математиков древности погиб от руки римского солдата, гордо воскликнув: «Отойди, не трогай моих чертежей!» Ответ: Греческий ученый – Архимед. Найдите пропавшие буквы: 1. ГМТР 2. ЗДЧ 3. ТРПЦ 4. ПРПНДКЛР Ответы: 1. Геометрия 2. Задача 3. Трапеция 4. Перпендикуляр.

Три в квадрате равно 9. четыре в квадрате равно 16. А чему равен угол в квадрате? (90º) Три в квадрате равно 9. четыре в квадрате равно 16. А чему равен угол в квадрате? (90º) Как называется треугольник, у которого две стороны равны? (равнобедренный) Может ли в треугольнике быть два тупых угла? (нет) Как называется прибор для измерения углов? (транспортир) Чему равна сумма углов треугольника? (180º) Как называются прямые, которые не пересекаются на плоскости? (параллельные) Как называется параллелограмм, у которого все стороны равны, а углы прямые? (квадрат) Как называется прибор для измерения отрезков? (линейка) Чему равна сумма смежных углов? (180º) Как называются прямые, которые пересекаются под прямым углом? (перпендикулярными)

Многие нерадивые ученики при выполнении домашнего задания задаются вопросом : «Зачем нужна геометрия? И вообще она мне не пригодиться!!! Зачем делать уроки! Да ладно!» И идут гулять! А ведь они даже не задумываются, как это пригодиться им в жизни! Как потом в дальнейшем они будут мучаться! Многие нерадивые ученики при выполнении домашнего задания задаются вопросом : «Зачем нужна геометрия? И вообще она мне не пригодиться!!! Зачем делать уроки! Да ладно!» И идут гулять! А ведь они даже не задумываются, как это пригодиться им в жизни! Как потом в дальнейшем они будут мучаться! Например: Будет такой ученик строителем, как он создаст план здания, если он не разбирается в геометрических фигурах, или не умеет находить их масштаб?? А если например, тот же ученик объяснял своему ребёнку этот предмет, что бы он сказал? Он бы плохо выглядел в глазах ребёнка и подавал ему плохой пример! Из этого можно сделать вывод, что без геометрии очень трудно жить!

Давайте попытаемся представить, что такой науки как геометрия не существует, а это значит, что человек не знает как называются фигуры! Давайте попытаемся представить, что такой науки как геометрия не существует, а это значит, что человек не знает как называются фигуры! А как так жить??? Вот например придёте вы в магазин, забудете название товара, как вы объясните, какой продукт вы хотите купить. Скорей всего продавец не поймёт такое объяснение, как жёлтое и вкусное! А как можно будет учиться в школе, как можно будет объяснять у доски какой формы земля, мяч???

Во всех слайдах я привела вам доказательства того, что геометрия нужна! Пусть мы используем её по мелочам и всё это может вам и не доказало, что геометрия нужна. Но есть такой вопрос, который заставляет любого скептика поверить в то, что она нужна! Зачем древние люди, греческие учёные, средневековые учёные изучали её? Доказывали свойства и теоремы??? Зачем сейчас мы её изучаем, если она нам не нужна. Ответ прост и элементарен – она нужна, так как без неё у нас не было бы ничего. Во всех слайдах я привела вам доказательства того, что геометрия нужна! Пусть мы используем её по мелочам и всё это может вам и не доказало, что геометрия нужна. Но есть такой вопрос, который заставляет любого скептика поверить в то, что она нужна! Зачем древние люди, греческие учёные, средневековые учёные изучали её? Доказывали свойства и теоремы??? Зачем сейчас мы её изучаем, если она нам не нужна. Ответ прост и элементарен – она нужна, так как без неё у нас не было бы ничего.

Большая советская энциклопедия. Большая советская энциклопедия. Собственные архивы. Энциклопедия «Кругосвет»