Презентация на тему: Задачи на параллелограмм


Определение: параллелограмм - четырехугольник, Определение: параллелограмм - четырехугольник, у которого противоположные стороны попарно параллельны.


Диагонали параллелограмма пересекаются и точкой пресечения делятся пополам. Диагонали параллелограмма пересекаются и точкой пресечения делятся пополам. Параллелограмм – выпуклый четырехугольник. У параллелограмма противолежащие стороны равны, противолежащие углы равны.

Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то такой четырехугольник – параллелограмм. Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то такой четырехугольник – параллелограмм. Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм. Если у четырехугольника противолежащие стороны попарно равны, такой четырехугольник – параллелограмм. Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм.

Высотой параллелограмма, проведенной к данной его стороне, называется перпендикуляр, опущенный из произвольной точки противолежащей стороны к прямой, содержащей данную сторону. Высотой параллелограмма, проведенной к данной его стороне, называется перпендикуляр, опущенный из произвольной точки противолежащей стороны к прямой, содержащей данную сторону.

Площадь параллелограмма равна произведению его стороны на проведенную к ней высоту: S = ah. Площадь параллелограмма равна произведению его стороны на проведенную к ней высоту: S = ah.

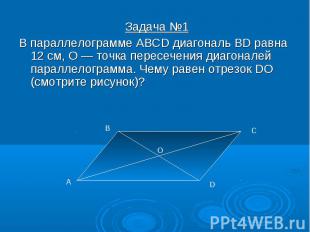
Задача №1 Задача №1 В параллелограмме ABCD диагональ BD равна 12 см, О — точка пересечения диагоналей параллелограмма. Чему равен отрезок DO (смотрите рисунок)?

Диагональ BD в параллелограмме ABCD точкой O делится пополам (свойство параллелограмма). Значит BO=OD=6 . Диагональ BD в параллелограмме ABCD точкой O делится пополам (свойство параллелограмма). Значит BO=OD=6 . Ответ: DO=6. Задача №2. В параллелограмме сумма двух углов равна 132°. Найдите градусную меру каждого из этих углов.

Эти углы не могут быть прилежащими к одной стороне, так как в этом случае бы их сумма была бы равна 180°: Значит, эти углы противолежащие. По свойству противолежащих углов параллелограмма они равны и каждый из них равен 66°. Эти углы не могут быть прилежащими к одной стороне, так как в этом случае бы их сумма была бы равна 180°: Значит, эти углы противолежащие. По свойству противолежащих углов параллелограмма они равны и каждый из них равен 66°. Ответ: 66°. Задача №3 Стороны параллелограмма 4 см и 6 см. Меньшая его высота равна 3 см. Вычислите второю высоту параллелограмма.

Площадь параллелограмма равна и . Так как S=aha= ah b , то меньшая высота соответствует большей стороне, значит меньшая высота опущена на сторону длиной 6 см. Значит S=18 см2 , а искомая высота равна и равна 4,5 см.

Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см. Решение: Пусть ABCD - данный параллелограмм, AK - указанная биссектриса, BK=7 , KC=14. Поскольку углы BKA, KAD, BAK равны , то треугольник ABK - равно- бедренный. Поэтому AB=BK=7, BC=BK+KC=21. Значит периметр равен 56.


Даны две окружности с общим центром в точке О, АС и BD — диаметры этих окружностей. Докажите, что четырехугольник ABCD — параллелограмм. Даны две окружности с общим центром в точке О, АС и BD — диаметры этих окружностей. Докажите, что четырехугольник ABCD — параллелограмм.

Доказательство. Так как О — центр концентрических окружностей, то диаметры АС и CD пересекаются и точкой пересечения делятся пополам, значит, ABCD — параллелограмм. Доказательство. Так как О — центр концентрических окружностей, то диаметры АС и CD пересекаются и точкой пересечения делятся пополам, значит, ABCD — параллелограмм.

Точки K и L - середины сторон AD и BC параллелограмма ABCD. Докажите, что прямые AL и CK делят диагональ BD на три равные части. Точки K и L - середины сторон AD и BC параллелограмма ABCD. Докажите, что прямые AL и CK делят диагональ BD на три равные части.

KD = AK, CL = BL. Так как ABCD - параллелограмм, то AD || BC, следовательно, AK || CL, причем AK = CL, так как AD = BC. Тогда по признаку параллелограмма имеем, что ALCK - параллелограмм. Следовательно, KM || AN и NL|| CM. Причем KM проходит через середину AD , а NL - через середину BC. Значит, KM - средняя линяя тр. ADN, а NL - cредняя линяя тр. BCM. Значит, DM = MN и BN = MN или DM = MN = BN. KD = AK, CL = BL. Так как ABCD - параллелограмм, то AD || BC, следовательно, AK || CL, причем AK = CL, так как AD = BC. Тогда по признаку параллелограмма имеем, что ALCK - параллелограмм. Следовательно, KM || AN и NL|| CM. Причем KM проходит через середину AD , а NL - через середину BC. Значит, KM - средняя линяя тр. ADN, а NL - cредняя линяя тр. BCM. Значит, DM = MN и BN = MN или DM = MN = BN.


Дан параллелограмм ABCD с острым углом при вершине A . На лучах AB и CB отмечены точки H и K соответственно так, что CH=BC и AK=AB . Дан параллелограмм ABCD с острым углом при вершине A . На лучах AB и CB отмечены точки H и K соответственно так, что CH=BC и AK=AB . а) Докажите, что DH=DK . б) Докажите, что треугольники DKH и ABK подобны.

Из равенства треугольников HCD и DAK (по двум сторонам и углу между ними) следует равенство отрезков DH и DK . Из равенства треугольников HCD и DAK (по двум сторонам и углу между ними) следует равенство отрезков DH и DK . Из равенства углов KAH и HCK следует, что точки A,C,H,K - лежат на одной окружности, а так как угол CKA и угол ADC в сумме 180 градусов , то на этой окружности лежит и точка D . Следовательно, углы KAB и KDH при вершинах A и D равнобедренных треугольников ABK и DKH равны. Поэтому треугольники подобны.

В параллелограмме ABCD диагональ AC больше диагонали BD . Точка M на диагонали AC такова, что около четырехугольника BCDM можно описать окружность. Докажите, что BD - общая касательная окружностей, описанных около треугольников ABM и ADM . В параллелограмме ABCD диагональ AC больше диагонали BD . Точка M на диагонали AC такова, что около четырехугольника BCDM можно описать окружность. Докажите, что BD - общая касательная окружностей, описанных около треугольников ABM и ADM .

Поскольку углы MBD, MCD, BAM равны, а точки A и D лежат по разные стороны от прямой BM , то BD - касательная к окружности, описанной около треугольника ABM . Поскольку углы MBD, MCD, BAM равны, а точки A и D лежат по разные стороны от прямой BM , то BD - касательная к окружности, описанной около треугольника ABM . Задача № 4 В параллелограмме ABCD с углом A , равным 60 градусов , проведена биссектриса угла B , пересекающая сторону CD в точке E . В треугольник ECB вписана окружность радиуса R . Другая окружность вписана в трапецию ABED . Найдите расстояние между центрами этих окружностей.

Пусть O1 и O2 - центры окружностей, вписанных в треугольник BCE и в ABED трапецию . Пусть O1 и O2 - центры окружностей, вписанных в треугольник BCE и в ABED трапецию . Треугольник O1EO2 - прямоугольный, т. к. угол O1EO2 - прямой (угол между биссектрисами смежных углов). Треугольник BCE - равносторонний (углы BEC, ABE, EBC равны между собой и равны 60 градусов ), O1E=2R , его высота EM равна 3R . Поэтому O2B=EM=3R . Тогда Следовательно, Ответ:

В параллелограмме лежат две окружности, касающиеся друг друга и трех сторон параллелограмма каждая. Радиус одной из окружностей равен 1. Известно, что один из отрезков стороны параллелограмма от вершины до точки касания равен . Найдите площадь параллелограмма. В параллелограмме лежат две окружности, касающиеся друг друга и трех сторон параллелограмма каждая. Радиус одной из окружностей равен 1. Известно, что один из отрезков стороны параллелограмма от вершины до точки касания равен . Найдите площадь параллелограмма.

Окружности равны. Расстояние между точками их касания с большей стороной параллелограмма равно сумме их радиусов, т. е. 2. Меньшая сторона параллелограмма видна из центра касающейся ее окружности под прямым углом. Один из отрезков этой стороны от вершины до точки касания равен , значит второй равен . Тогда большая сторона равна Окружности равны. Расстояние между точками их касания с большей стороной параллелограмма равно сумме их радиусов, т. е. 2. Меньшая сторона параллелограмма видна из центра касающейся ее окружности под прямым углом. Один из отрезков этой стороны от вершины до точки касания равен , значит второй равен . Тогда большая сторона равна Следовательно, площадь параллелограмма равна 2( ).

В параллелограмме ABCD острый угол равен . Окружность радиуса r проходит через вершины A,B,C и пересекает прямые AD и CD в точках M и N . Найдите площадь треугольника BMN . В параллелограмме ABCD острый угол равен . Окружность радиуса r проходит через вершины A,B,C и пересекает прямые AD и CD в точках M и N . Найдите площадь треугольника BMN .