Презентация на тему: Координатный метод в пространстве

Метод координат в пространстве Координаты точки и координаты вектора 5klass.net

Прямоугольная система координат в пространстве Если через точку пространства проведены три попарно перпендикулярные прямые, на каждом из них выбрано направление(оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве. Рассмотрим рисунок

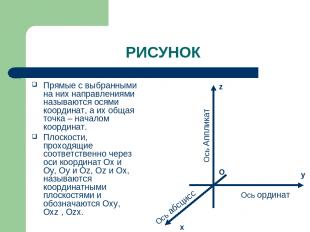
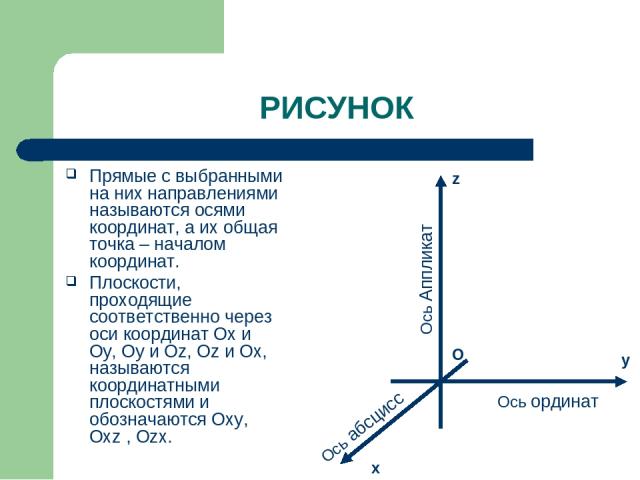
РИСУНОК Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат. Плоскости, проходящие соответственно через оси координат Ох и Оy, Oу и Оz, Oz и Ox, называются координатными плоскостями и обозначаются Oxy, Oхz , Ozх. Ось Аппликат Ось абсцисс Ось ординат y z O x

Определение луча на координатной плоскости. Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч – отрицательной полуосью.

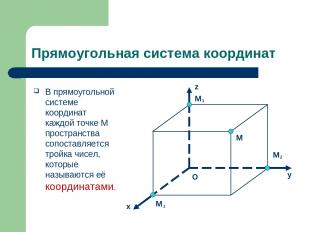
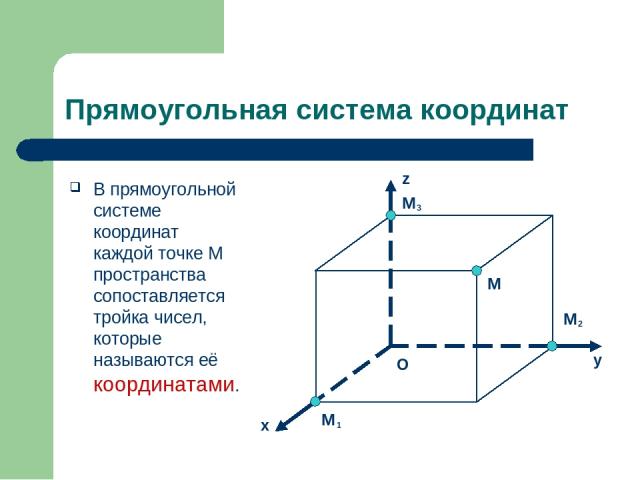
Прямоугольная система координат В прямоугольной системе координат каждой точке M пространства сопоставляется тройка чисел, которые называются её координатами. y z x M 1 M 2 M 3 M O

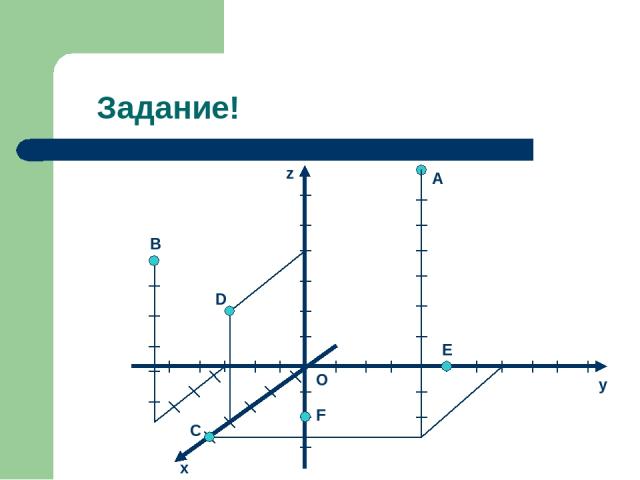
Нахождение точки на координатной плоскости. Если, например, точка M лежит на координатной плоскости или на оси координат, то некоторые её координаты равны нулю. Так, если M принадлежит Oxy, то аппликата точка M равна нулю: z=0. Аналогично если M принадлежит Oхz, то y=0, а если M принадлежит Oyz, то x=0. Если M принадлежит Ox, то ордината и аппликата точки M равна нулю: y=0 и z=0. Если M принадлежит Oy, то x=0 и z=0; если M принадлежит Oz, то x=0 и y=0. Все три координаты начала координат равны нулю: О (0;0;0). Напиши координаты для точек A, B, C, D, E, F на рисунке следующего слайда.

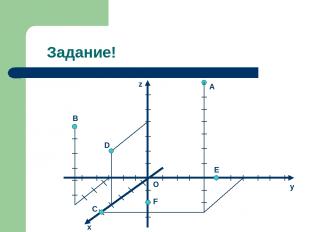
Задание! B C O E F D z y x A

Ответы. A(5; 4; 10), B(4; -3; 6), C(5; 0; 0), D(4; 0; 4), E(0; 5; 0), F(0; 0; -2). Сравни свои ответы.

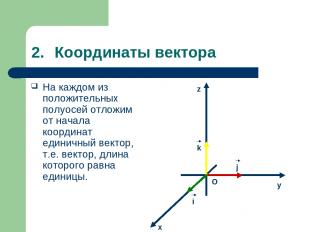
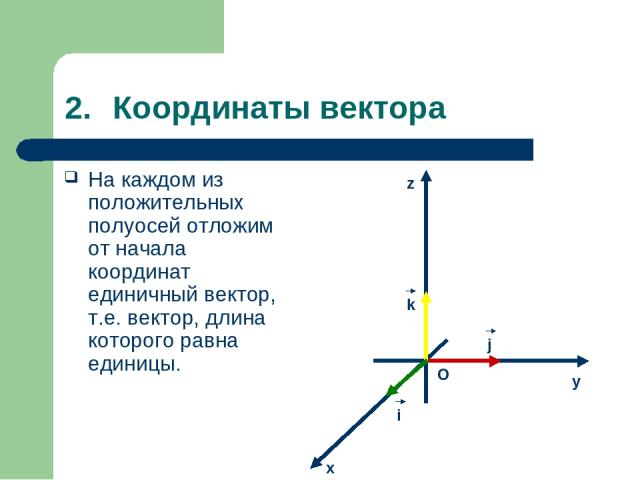
Координаты вектора На каждом из положительных полуосей отложим от начала координат единичный вектор, т.е. вектор, длина которого равна единицы. j k i y z x O

Разложение по координатным векторам Любой вектор a можно разложить по координатным векторам, т.е. представить в виде а = xi + yj + zk Причем коэффициенты разложения x, y, z определяются единственным образом.

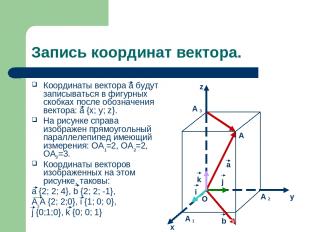
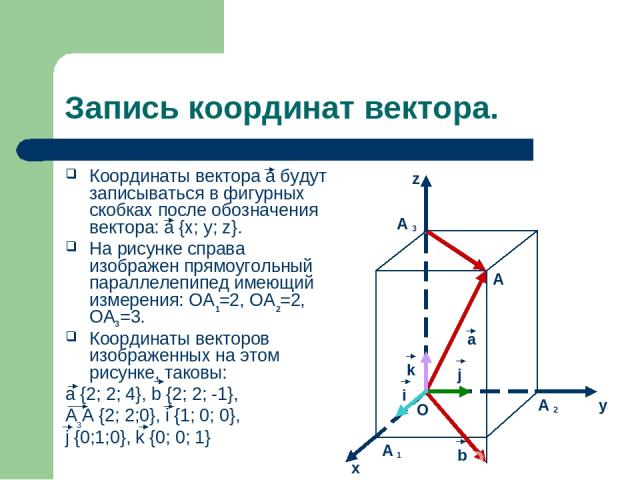
Запись координат вектора. Координаты вектора а будут записываться в фигурных скобках после обозначения вектора: а {x; y; z}. На рисунке справа изображен прямоугольный параллелепипед имеющий измерения: OA =2, OA =2, OA =3. Координаты векторов изображенных на этом рисунке, таковы: a {2; 2; 4}, b {2; 2; -1}, A A {2; 2;0}, i {1; 0; 0}, j {0;1;0}, k {0; 0; 1} A A A A O y x z a j i k b 3 2 1 1 2 3 3

Нулевой вектор и равные вектора Так как нулевой вектор можно представить в виде 0 = 0i + 0j + 0k, то все координаты нулевого вектора равны нулю. Координаты равных векторов соответственно равны, т.е. если векторы a {x ; y ; z } и b {x ; y ; z } равны, то x =x , y =y и z =z . 1 1 1 2 2 2 1 2 1 2 1 2

Правила нахождения суммы, разности и произведения на данное число. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Если a {x ; y ; z } и b {x ; y ; z } – данные векторы, то вектор a + b имеет координаты {x +x ; y +y ; z +z } 1 2 1 2 1 2 2 2 2 1 1 1

Правило №2 Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Если a {x ; y ; z } и b {x ; y ; z } – данные векторы, то вектор a – b имеет координаты {x –x ; y –y ; z –z } 1 2 1 2 1 2 1 2 1 1 2 2

Правило №3 Каждая координата произведения вектора на число равна произведение соответствующей координаты вектора на это число. Если a {x; y; z } – данный вектор, α - данное число, то вектор αa имеет координаты { x; y; z} α α α

Связь между координатами векторов и координатами точек. Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус-вектором данной точки. Координаты любой точки равны соответствующим координатам её радиус-вектора. Каждая координата вектора равна разности соответствующих координат его конца и начала.

Простейшие задачи в координатах Каждая координата середины отрезка равна полусумме соответствующих координат его концов. Длина вектора a {x; y; z} вычисляется по формуле |a| = √x² + y² + z²

Расстояние между точками Расстояния между точка M (x ; y ; z ) и M (x ; y ; z ) вычисляется по формуле d = √(x – x )² + (y – y )² + (z – z )² 1 2 2 2 2 1 1 1 2 1 2 1 2 1

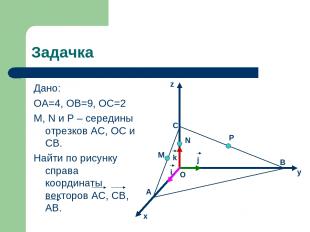
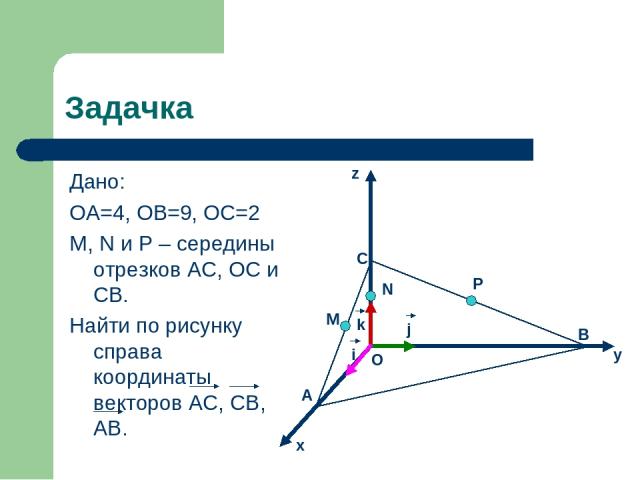
Задачка Дано: ОА=4, ОВ=9, ОС=2 M, N и P – середины отрезков AC, OC и CB. Найти по рисунку справа координаты векторов AC, CB, AB. P B y N j i k M O C A x z

Решение: AC = AO + OC = 4i + 2k, AC {-4; 0; 2} CB = CO + OB = 2k + 9j, CB {0; 9; 2} AB = AO + OB = -4i + 9j, AB {-4; 7; 0}

Спасибо за внимание!!! Презентация сделана по учебнику геометрии для 10 -11 класса Авторы: Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Л. С. Киселёва, Э. Г. Позняк Издание подготовлено под научным руководством академика А. Н. Тихонова. Презентацию делал: Ученик 11 “A” класса, ХСОШ №5, города Хотьково Витушки Сергей Валерьевич. Классный руководитель: Шмелёва Ольга Владимировна.