Презентация на тему: Конус и усечённый конус

Понятие конуса. Площадь поверхности конуса. Усеченный конус. 900igr.net

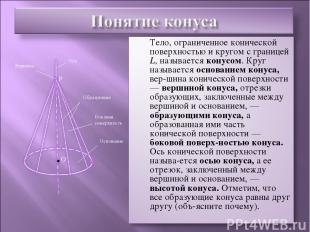
P Ось Вершина Образующие Боковая поверхность Основание

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. На рисунке изображен конус, полученный вращением прямоугольного треугольника ABC вокруг катета АВ. При этом боковая поверхность конуса образуется вращением гипотенузы АС, а основание — вращением катета ВС. А С

Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О и расположенным на оси, конуса. Радиус r1 этого круга равен (ОР/РО1)*r, где r - радиус основания конуса, что легко усмотреть из подобия прямоугольных треугольников РОМ и РО1М1. P M О1 r r1 M1 α

Р А Р А В А|

За площадь боковой поверхности конуса принимается площадь ее развертки. Выразим площадь Sбoк боковой поверхности конуса через его образу ющую I и радиус основания r. Площадь кругового сектора — развертки боковой поверхности конуса равна πl2α 360 Где α – градусная мера дуги АВАI , поэтому

Sбок = πl2α 360 (1)

α = 360 r l

Подставив это выражение в формулу (1), получим (2)

Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Для вычисления площади SКОН полной поверхности конуса получается формула

P О1 r1 Основание Образующая Основание r Боковая поверхность

С В А D

P A О1 r1

(3)

PA 1 PA = r 1 r или PA 1 + l Отсюда получаем PA 1 = r 1 r PA 1 = l r 1 r - r 1