Презентация на тему: Как доказать истину в геометрии?

Докажи!!! Исследовательская работа по геометрии, 7 класс.

Как доказать истину в геометрии? Авторы: учащиеся 7Д класса МОУ «Средняя общеобразовательная школа №2 города Кувандыка Оренбургской области»

Цель исследования: Найти с помощью чего и как в геометрии доказывается истинность того или иного математического утверждения?

Вопросы исследования: Что такое геометрия? Строим дом под названием «Геометрия». Для чего нужна геометрия? Примеры доказательств.

Возникновение геометрии. Слово «ГЕОМЕТРИЯ» древнегреческого происхождения. ГЕОМЕТРИЯ – гео- «земля», метрио- «измеряю». Причина возникновения: практическая деятельность людей (различные измерительные работы при: разметке земельных участков,проведении дорог, строительстве зданий,…). ГЕОМЕТРИЯ, раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения.

Разделы курса геометрия

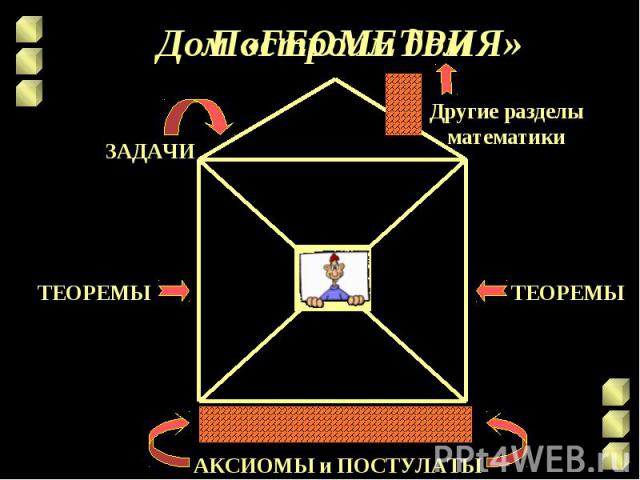
Дом «ГЕОМЕТРИЯ»

Аксиомы и постулаты. Существует набор исходных посылок, называемых аксиомами и постулатами, на которых базируется вся структура геометрии. АКСИОМЫ – это утверждения, принимаемые за истинные без доказательств. Аксиомы обычно подразделяются на две группы: общие, относящиеся ко всей математике, и геометрические.

Легенда “О происхождении аксиом.” Было это в Древнем Египте. Огромная река течет через всю эту местность — Нил. Разливаясь с каждой весной, Нил затоплял поля и уничтожал межи, разделявшие земельные участки. Межи приходилось восстанавливать каждый раз заново. Из года в го, из века в век совершенствовались приемы землемерия. Если произнести это слово на древнегреческом языке, мы узнаем в нем название науки, о которой рассуждаем: геометрия. Натягивая межевую веревку между двумя колышками, древние землемеры не раз имели возможность убедиться, что это несложная операция всегда приводит к одному и тому же результату. Многократно повторенный опыт внушал вывод: Через две точки можно провести прямую, и притом только одну. Так рождались аксиомы, общие для всех, к то трудиться на земле.

Аксиомы и постулаты. К числу геометрических аксиом относятся, например, следующие:

Подумай… Задание 1. У Вас в наличии малярная кисть, плакатное перо и тонко очиненный карандаш. Каким из этих инструментов вы бы воспользовались, чтобы нарисовать прямую линию на бумаге? (Посмотрите на след через лупу, анализируйте ответ и сделайте вывод).

Аксиомы и постулаты. Следующий ПОСТУЛАТ касается построений и принимается за истину без доказательств:

Теоремы. На основе аксиом и определений чисто логическим путем выводятся новые утверждения о первичных и определяемых понятиях. Получаемые новые утверждения называются ТЕОРЕМАМИ

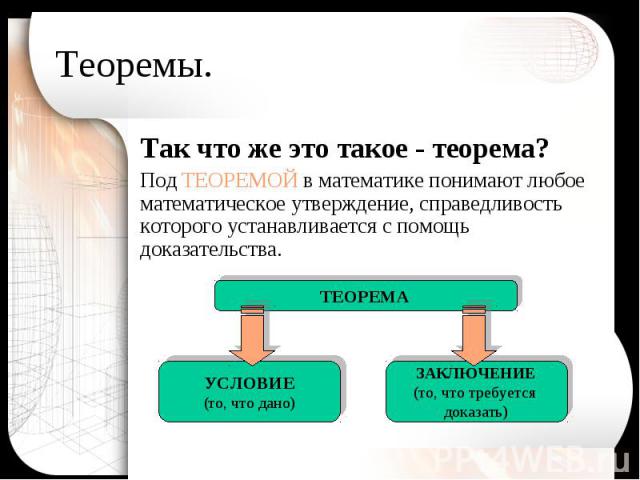
Теоремы. Так что же это такое - теорема? Под ТЕОРЕМОЙ в математике понимают любое математическое утверждение, справедливость которого устанавливается с помощь доказательства.

Доказательство. Когда же появились первые доказательства? И тут сквозь дым времен перед нами предстает удивительный человек, знаменитый мудрец из древнегреческого города Милет. С поразительным единодушием историки науки присваивают звание первоматематика Фалесу Милетскому (625-527 гг. до н.э.).

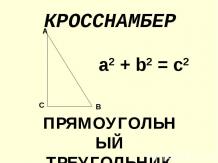
Теоремы. Теорема. Вертикальные углы равны. Дано: AOB и COD – вертикальные. Доказать: AOB = COD. Доказательство. Так как AOB и COD – вертикальные, то лучи OB и OD – дополнительные, следовательно, AOB и AOD – смежные. Аналогично, COD и AOD – смежные. По свойству смежных углов: AOB + AOD = 180 и COD + AOD = 180 . Имеем: AOB = 180 – AOD и COD = 180 – AOD, значит, AOB = COD, ч. т. д.

ТЕСТ.

Вывод Математическое доказательство истины в геометрии проводится по четко определенным правилам. Исходя из аксиом, ранее известных фактов и теорем, в соответствии с законами логики устанавливается справедливость новой теоремы, решаются задачи.

Рекомендуем: Энциклопедический словарь юного математика. Геометрия 7-9 ( Атанасян Л. С.) 2. История математики в древности и в средние века. М.; Л., 1932. 3. История математики с древнейших времен до начала ХIХ столетия /Под ред. А. П. Юшкевича./ М., 1970. http://www.college.ru/mathematics/courses/planimetry/content/chapter16/section/paragraph4/theory.html http://www.refal.net/turchin/phenomenon/chapter10.htm http://www.bestreferat.ru/referat-46420.html