Презентация на тему: Цветы из сада геометрии

(фантазия на тему «МНОГОГРАННИКИ») «В огромном саду геометрии каждый найдет букет себе по вкусу.» Д. Гильберт

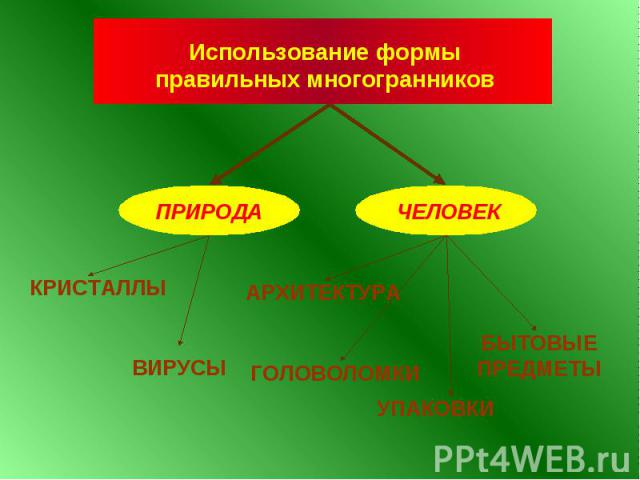
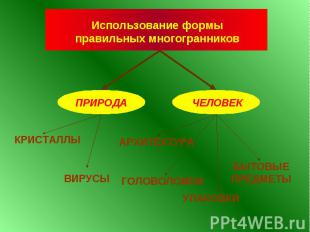
ПЛАН ИЗУЧЕНИЯ ТЕМЫ Определение правильного выпуклого многогранника. Платоновы тела, их виды. Формула Эйлера для выпуклых многогранников. Формулы для вычисления объема и площади поверхности правильных многогранников. Использование формы правильных многогранников природой и человеком. Звездчатые многогранники, их виды. Архимедовы тела, их виды.

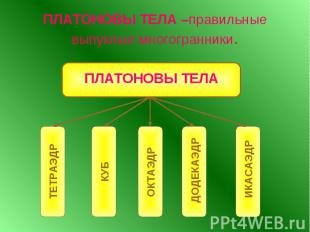
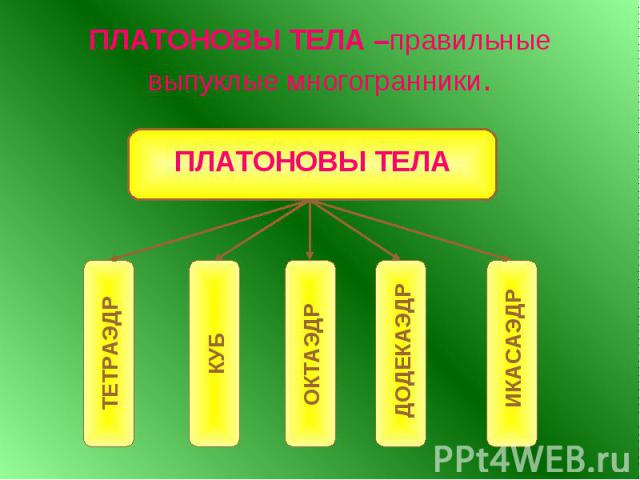
ПЛАТОНОВЫ ТЕЛА –правильные выпуклые многогранники.

ПРАВИЛЬНЫЙ МНОГОГРАННИК- выпуклый многогранник, грани которого являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине которого сходится одно и то же число ребер.

ФОРМУЛЫ ДЛЯ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ

ТЕТРАЭДР

КУБ (ГЕКСАЭДР)

ОКТАЭДР

ДОДЕКАЭДР

ИКОСАЭДР

Леонард Эйлер (1707 – 1783 гг.) немецкий математик и физик

Платон 428 (427) – 348 (347) гг. до нашей эры

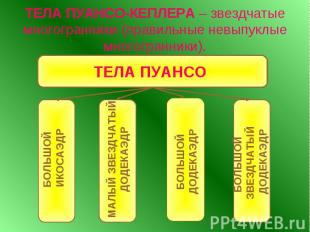
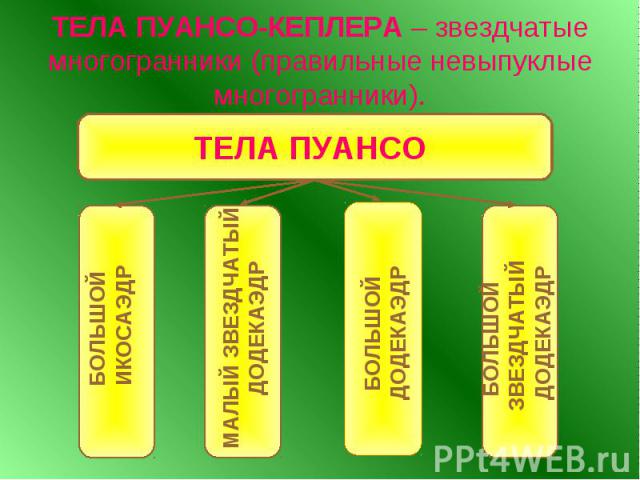
ТЕЛА ПУАНСО-КЕПЛЕРА – звездчатые многогранники (правильные невыпуклые многогранники).

Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Два из них знал И. Кеплер (1571 – 1630 гг.). В 1812 году французский математик О. Коши доказал, что кроме пяти «платоновых тел» и четырех «тел Пуансо» больше нет правильных многогранников.

БОЛЬШОЙ ИКОСАЭДР

МАЛЫЙ ЗВЕЗДЧАТЫЙ ДОДЕКАЭДР

БОЛЬШОЙ ДОДЕКАЭДР

БОЛЬШОЙ ЗВЕЗДЧАТЫЙ ДОДЕКАЭДР

ГРАВЮРА ГОЛАНДСКОГО ХУДОЖНИКА МАУРИЦА КОРНЕЛИУСА ЭШЕРА «СИЛЫ ГРАВИТАЦИИ»

Иоганн Кеплер (1571 – 1630 гг.)

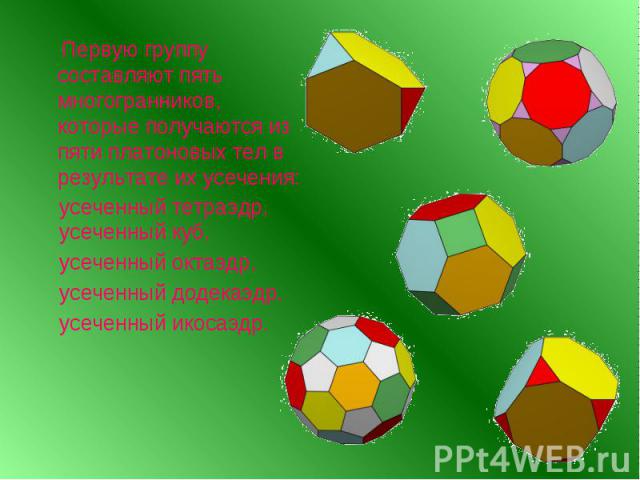
ТЕЛА АРХИМЕДА –полуправильные однородные выпуклые многогранники Архимедовыми телами называются выпуклые многогранники, все многогранные углы которых равны, а грани - правильные многоугольники нескольких типов (этим они отличаются от платоновых тел). Множество архимедовых тел можно разбить на пять групп.

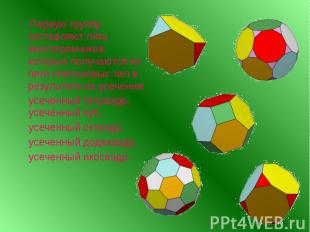
Первую группу составляют пять многогранников, которые получаются из пяти платоновых тел в результате их усечения: Первую группу составляют пять многогранников, которые получаются из пяти платоновых тел в результате их усечения:

Вторую группу составляют два тела, называемых квазиправильными многогранниками. Это название означает, что гранями этого многогранника являются правильные многоугольники всего двух типов, причем каждая грань одного типа окружена гранями другого типа. Эти два тела называются Вторую группу составляют два тела, называемых квазиправильными многогранниками. Это название означает, что гранями этого многогранника являются правильные многоугольники всего двух типов, причем каждая грань одного типа окружена гранями другого типа. Эти два тела называются

В третью группу входят В третью группу входят

Для них характерно несколько повернутое положение граней. В результате эти многогранники, в отличие от предыдущих, не имеют плоскостей симметрии, но имеют оси симметрии. Так как плоскостей симметрии нет, то зеркальное отражение такого тела не совпадает с исходным телом, и поэтому существуют по две формы каждого из них - "правая" и "левая", отличающиеся так же, как правая и левая руки. Для них характерно несколько повернутое положение граней. В результате эти многогранники, в отличие от предыдущих, не имеют плоскостей симметрии, но имеют оси симметрии. Так как плоскостей симметрии нет, то зеркальное отражение такого тела не совпадает с исходным телом, и поэтому существуют по две формы каждого из них - "правая" и "левая", отличающиеся так же, как правая и левая руки.

открытого лишь в XX веке. Он может быть получен из ромбокубоктаэдра, если повернуть одну из восьмиугольных чаш на 45°. открытого лишь в XX веке. Он может быть получен из ромбокубоктаэдра, если повернуть одну из восьмиугольных чаш на 45°.

Архимед около 287 – 212 гг. до нашей эры

Список литературы: М. Венниджер «Модели многогранников», изд. «Мир», Москва, 1974 г. К. Левитин «Геометрическая рапсодия», изд. «Знание», Москва, 1984 г. Журнал «Квант», №4 ,1987 г. Интернетресурсы: http://nips.riss-telecom.ru/poli/