Презентация на тему: Геометрические вариации на «пчелиную» тему.

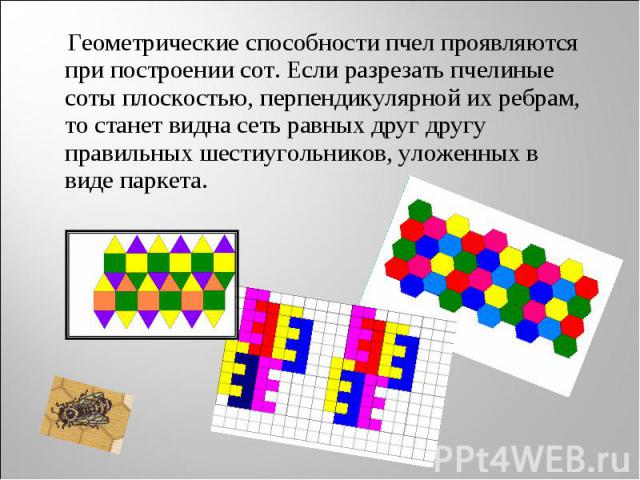
Геометрические способности пчел проявляются при построении сот. Если разрезать пчелиные соты плоскостью, перпендикулярной их ребрам, то станет видна сеть равных друг другу правильных шестиугольников, уложенных в виде паркета. Геометрические способности пчел проявляются при построении сот. Если разрезать пчелиные соты плоскостью, перпендикулярной их ребрам, то станет видна сеть равных друг другу правильных шестиугольников, уложенных в виде паркета.

Выполняя несложные расчеты, убеждаемся, что такими многоугольниками могут быть только правильные треугольники, квадраты или правильные шестиугольники. Выполняя несложные расчеты, убеждаемся, что такими многоугольниками могут быть только правильные треугольники, квадраты или правильные шестиугольники.

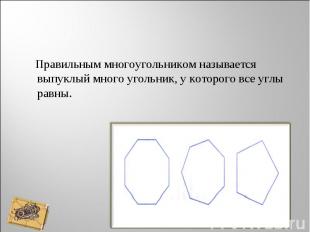
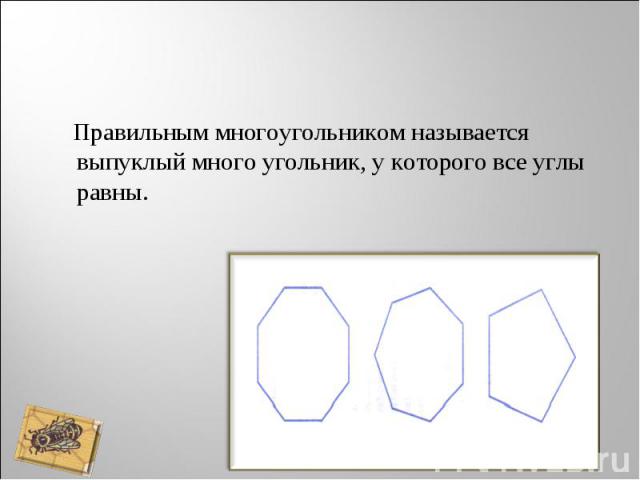
Правильным многоугольником называется выпуклый много угольник, у которого все углы равны. Правильным многоугольником называется выпуклый много угольник, у которого все углы равны.

Для того чтобы выяснить, почему пчела строит соты, перпендикулярное сечение которых есть правильный шестиугольник, а не правильный треугольник или квадрат, рассматривается вспомогательная задача Для того чтобы выяснить, почему пчела строит соты, перпендикулярное сечение которых есть правильный шестиугольник, а не правильный треугольник или квадрат, рассматривается вспомогательная задача

Даны три равновеликие друг другу фигуры — правильный треугольник, квадрат и правильный шестиугольник. Какая из данных фигур имеет наименьший периметр? Даны три равновеликие друг другу фигуры — правильный треугольник, квадрат и правильный шестиугольник. Какая из данных фигур имеет наименьший периметр? Решение

Действительно, сумма внутренних углов выпуклого n-угольника равна (n-2)*180°, где n-число сторон многоугольника. Сумма углов, сходящихся в одной вершине паркета, равна 360°. Действительно, сумма внутренних углов выпуклого n-угольника равна (n-2)*180°, где n-число сторон многоугольника. Сумма углов, сходящихся в одной вершине паркета, равна 360°.

Тогда (n-2)*180°/n*k=360°. Отсюда k=2n/(n-2). Тогда (n-2)*180°/n*k=360°. Отсюда k=2n/(n-2). Если n=3, то k=6, т.е. в одной вершине паркета могут сходиться 6 правильных треугольников. Если n=4,то k=4 т.е. в одной вершине паркета могут сходится 4 квадрата. Если n=5,то k=3.3т.е. не существует паркета из правильных пятиугольников. Если n=6,то k=3т.е. в одной вершине паркета могут сходится 3 правильных шестиугольника. Если n=7,то k=2.8т.е. не существует паркета из правильных семиугольников. Итак далее.

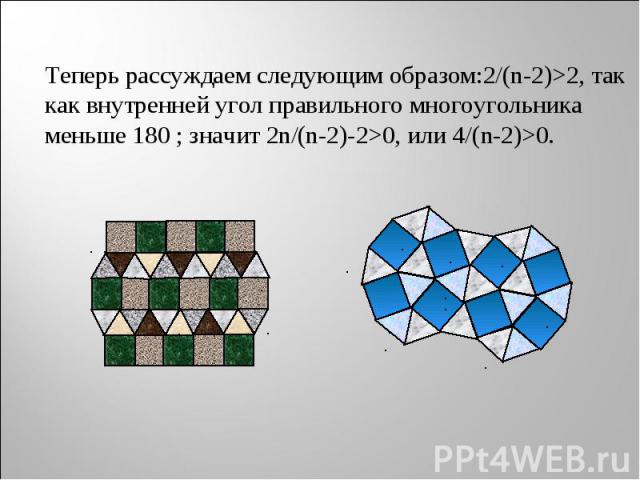
Теперь рассуждаем следующим образом:2/(n-2)>2, так как внутренней угол правильного многоугольника меньше 180 ; значит 2n/(n-2)-2>0, или 4/(n-2)>0. Теперь рассуждаем следующим образом:2/(n-2)>2, так как внутренней угол правильного многоугольника меньше 180 ; значит 2n/(n-2)-2>0, или 4/(n-2)>0.

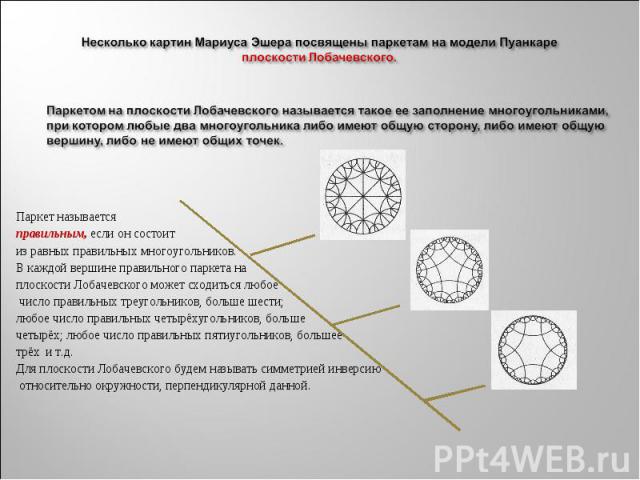
Знаменитый голландский художник Мариус Эшер (1898 – 1972) посвятил паркетам несколько своих картин. Знаменитый голландский художник Мариус Эшер (1898 – 1972) посвятил паркетам несколько своих картин.

Паркет называется правильным, если он состоит из равных правильных многоугольников. В каждой вершине правильного паркета на плоскости Лобачевского может сходиться любое число правильных треугольников, больше шести; любое число правильных четырёхугольников, больше четырёх; любое число правильных пятиугольников, большее трёх и т.д. Для плоскости Лобачевского будем называть симметрией инверсию относительно окружности, перпендикулярной данной.

1.http// www.tymen-lechnopfrk.ru 1.http// www.tymen-lechnopfrk.ru 2.http//www.vip.km.ru/vschool/ 3. Глухова А. Правильные многоугольники в природе. Математика. Еженедельное учебно-методическое приложение к газете « Первое сентября», № 38, 1999. 4.Фирсина С. Правильные многоугольники. Математика. Еженедельное учебно-методическое приложение к газете « Первое сентября», № 10, 2000. 5.Шарыгин И.Ф. Ерганжиева Л.Н. Наглядная геометрия. Учебное пособие для 5-6 классов. - М.: МИРОС, 1992. 6.Зоология 6-7калсс.2006г. 7.Лечение пчелиным мёдом и ядом. 8.Математика в школе. Научно-теоретический и методический журнал. Геометрические вариации на «пчелиную» тему.