Презентация на тему: Определенные треугольники и их виды

Геометрия

Содержание Треугольники. Определение треугольника. Виды треугольников. Медианы, биссектрисы и высоты треугольника. Признаки равенства треугольников

Определение треугольника Треугольником называется геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки. ∆ ABC, ∆ BCA, ∆ CAB A,B,C – вершины треугольника. ∟А, ∟B, ∟C – углы треугольника. AB, BC, CA – стороны треугольника.

Равенство треугольников Два треугольника называются равными, если их можно совместить наложением. ∆ ABC = ∆ A1B1С1 ∟А = ∟А1, ∟B = ∟B1, ∟C = ∟C1. AB=AB1, BC=BC1, CA=CA1

Виды треугольников (по сторонам) ∆ MNK – равносторонний MN=NK=KM ∆ ABC – равнобедренный АВ=ВС ∆ EDF – разносторонний

Виды треугольников (по углам) ∆ ABC – тупоугольный ∟C - тупой ∆ DEC – остроугольный ∆ MLK – прямоугольный ∟K - прямой

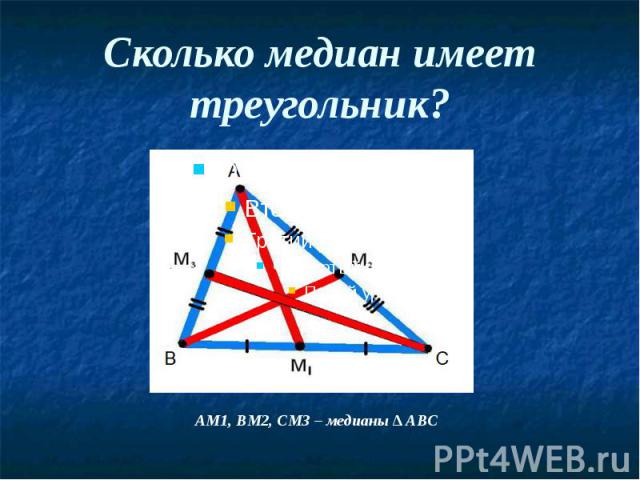
Медианы треугольника Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
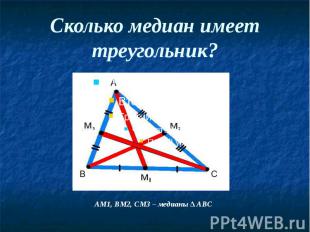
Сколько медиан имеет треугольник?

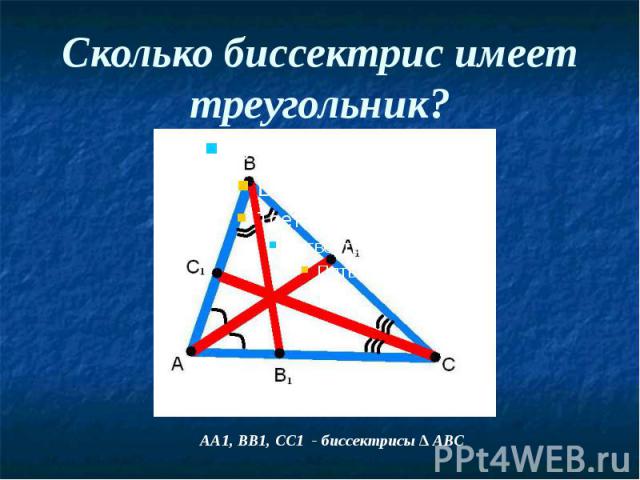
Биссектрисы треугольника Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
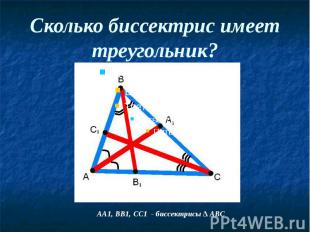
Сколько биссектрис имеет треугольник?

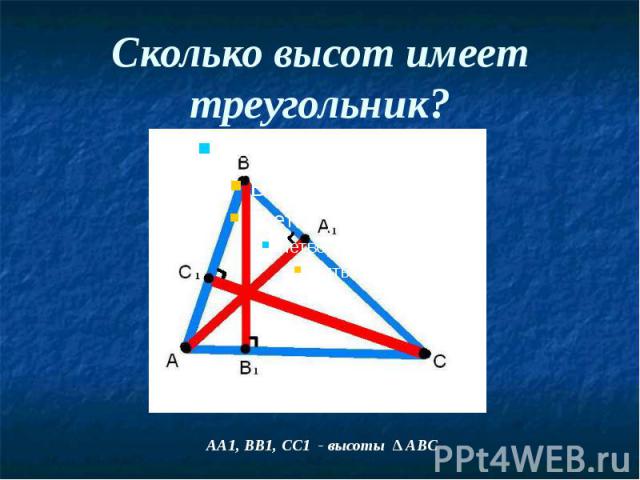
Высоты треугольника Перпендикуляр, проведенный из вершины треугольника к прямой, содержащий противоположенную сторону, называется высотой треугольника.
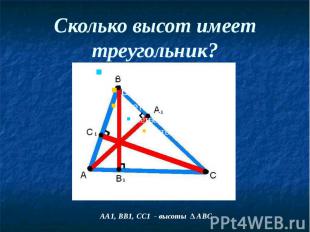
Сколько высот имеет треугольник?

Первый признак равенства треугольников Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников Если одна сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.