Презентация на тему: Задачи на построение сечений

10 А класс МОУ СОШ №154 Учитель: Колоскова Людмила Леонтьевна

Тема урока: Задачи на построение сечений Цель урока: Развивать умение решать задачи на построение сечений. Развивать пространственное воображение учащихся. Воспитывать интерес к предмету.

Повторение Какие фигуры могут быть сечения тетраэдра, параллелепипеда? Какое свойство учитывается при построении сечения параллелепипеда?

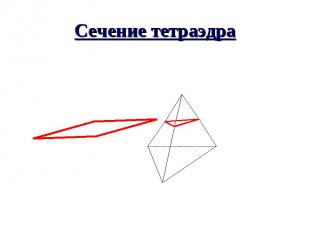
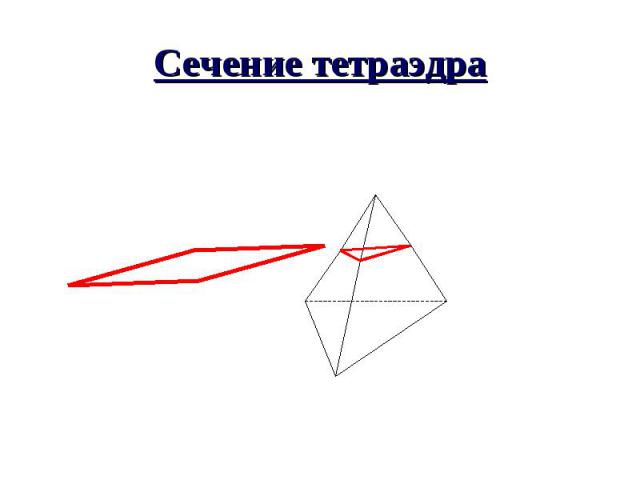
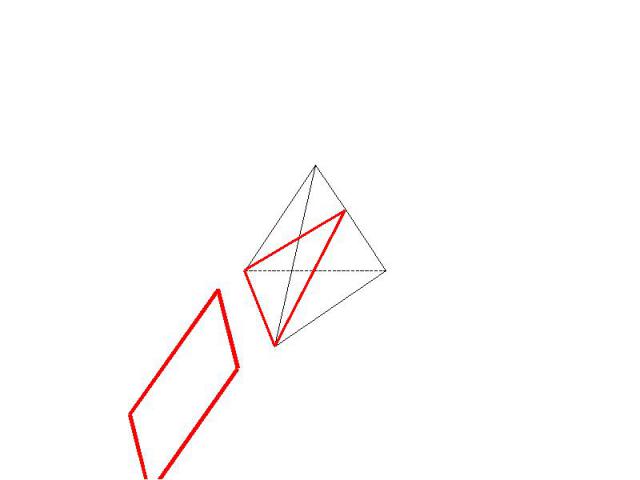
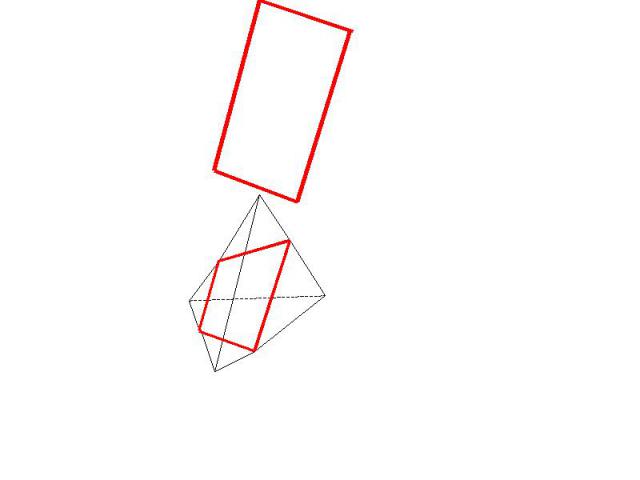
Сечение тетраэдра

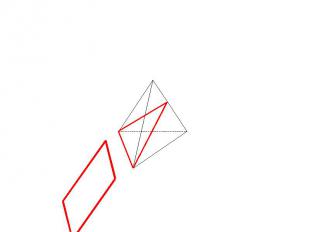
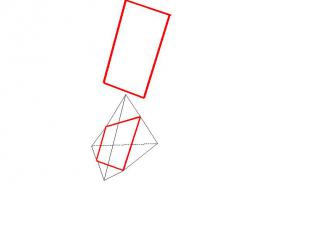
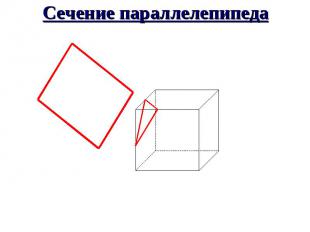
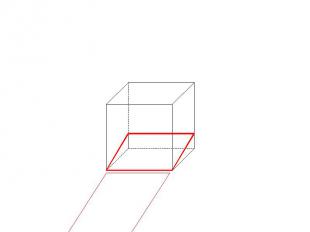
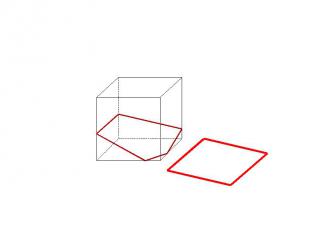
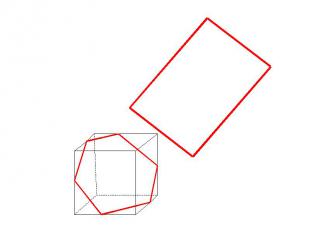
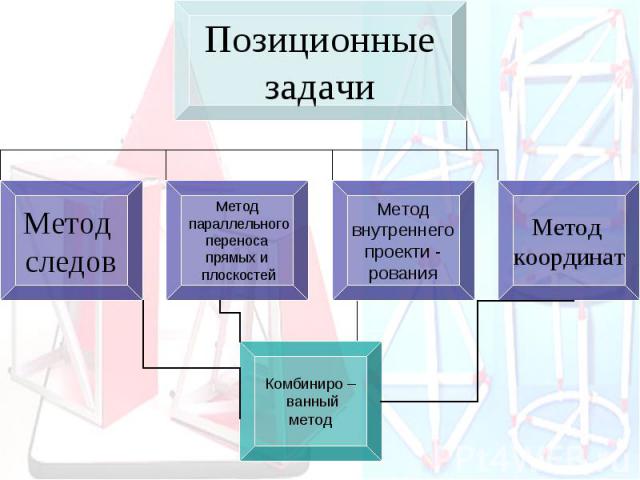
Основные методы построения сечений Позиционные (даны фигуры, но не даны размеры) Метрические (даны размеры)

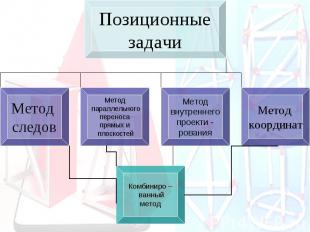
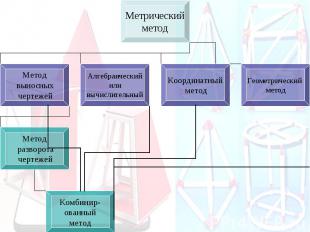
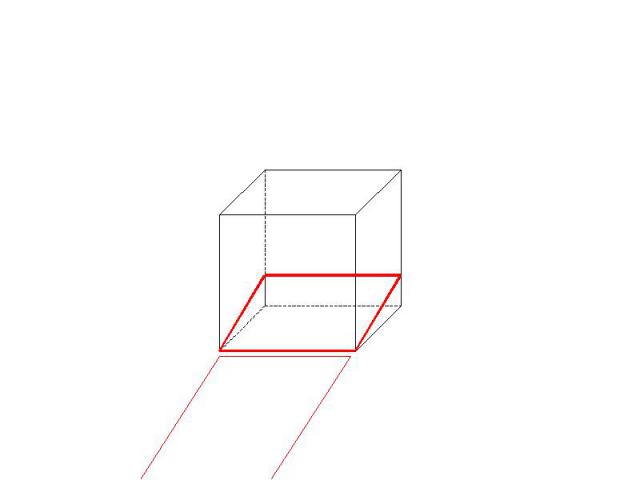
Остановимся более подробно на позиционных методах Метод следов: Применяется в тех случаях, когда секущая плоскость задана: - тремя точками - точкой и прямой - двумя пересекающимися прямыми

Суть метода Находят след секущей плоскости, т.е. прямую пересечения секущей плоскости и плоскостью какой-либо грани

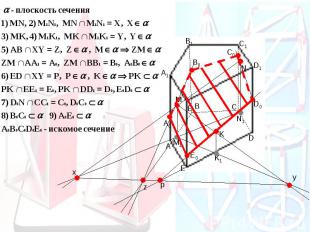
Метод внутреннего проектирования Задача и сфера применения этого метода такая же, как и у предыдущего

Суть метода Прямые секущей плоскости проектируются на плоскость основания

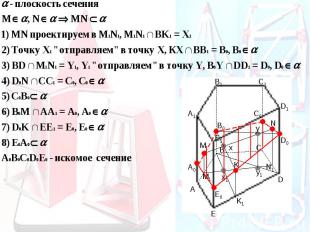
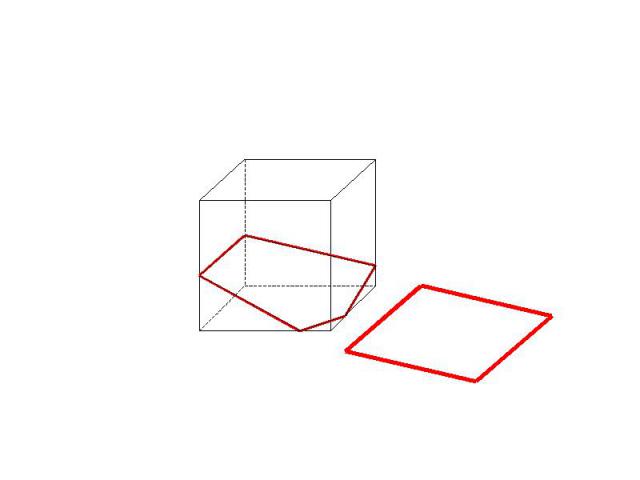
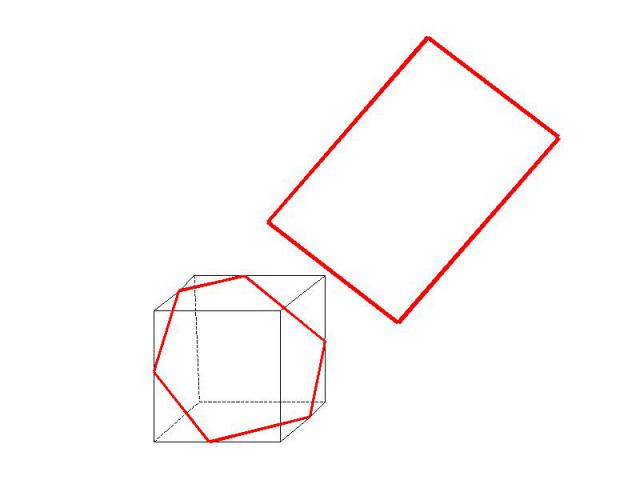
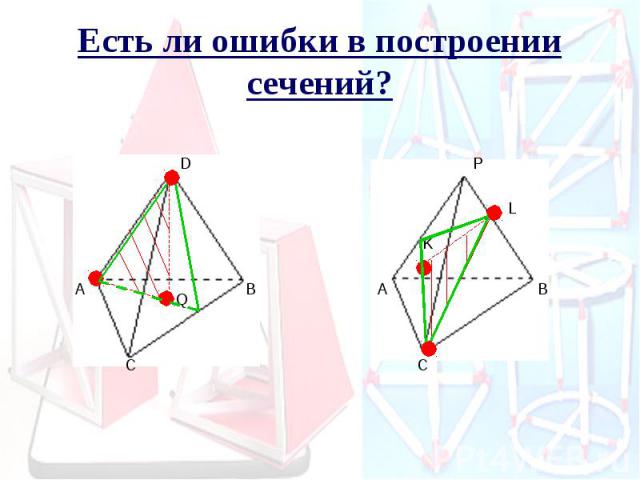
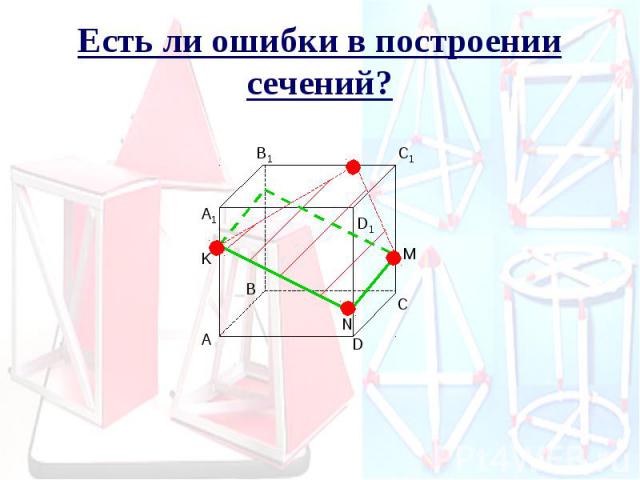
Есть ли ошибки в построении сечений?

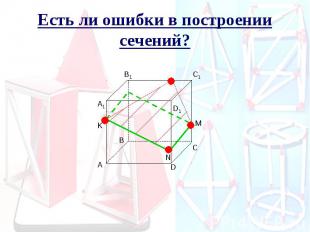
Есть ли ошибки в построении сечений?

Задачи на построение сечений РАВС – правильный тетраэдр, точка Q – центр грани АВС, точка К – середина ребра АВ. Постройте сечение тетраэдра плоскостями: а) АРQ б) КРQ Начертите общий отрезок этих сечений.

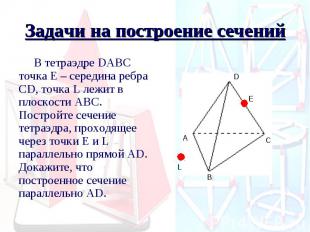
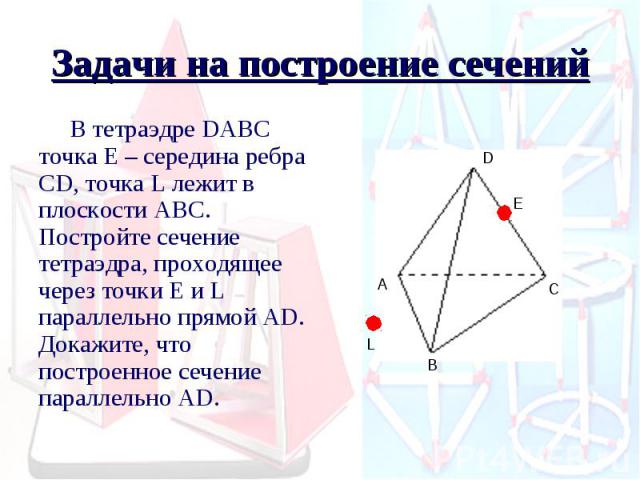
Задачи на построение сечений В тетраэдре DАВС точка Е – середина ребра СD, точка L лежит в плоскости АВС. Постройте сечение тетраэдра, проходящее через точки Е и L параллельно прямой АD. Докажите, что построенное сечение параллельно АD.

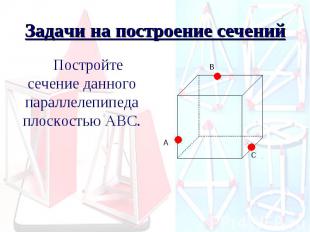
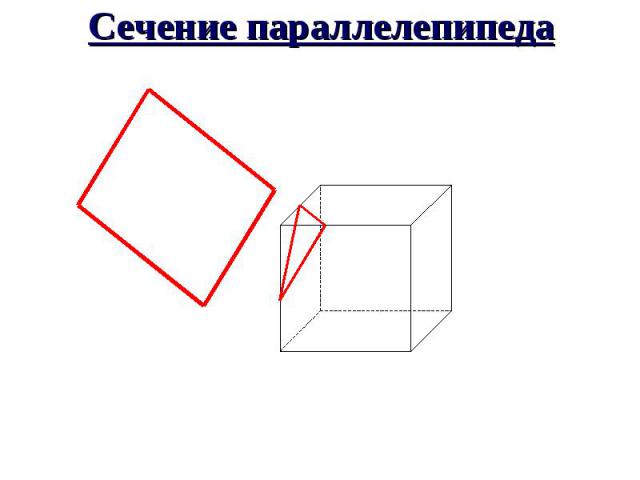
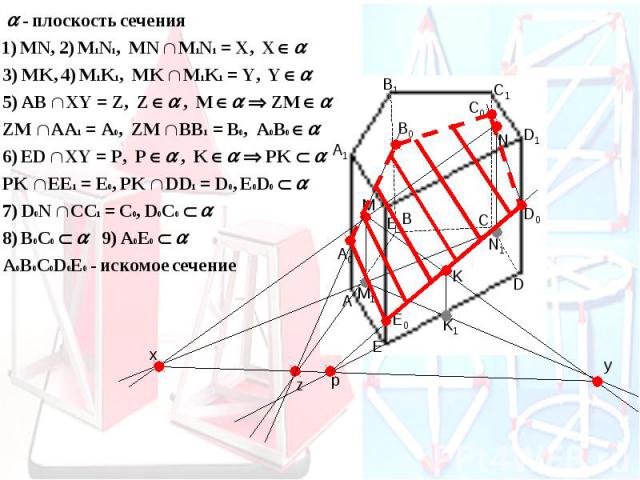
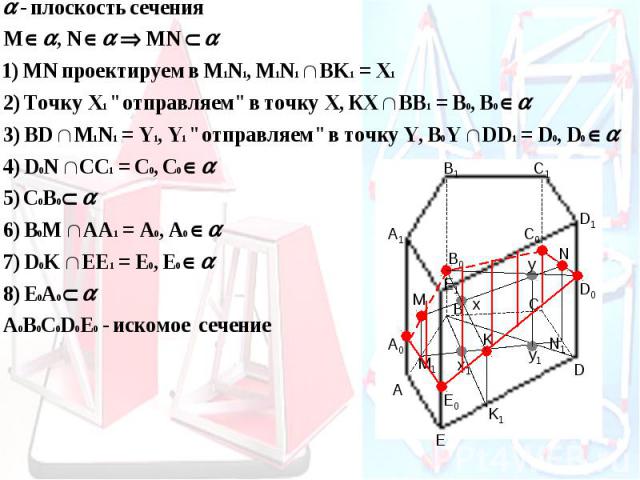
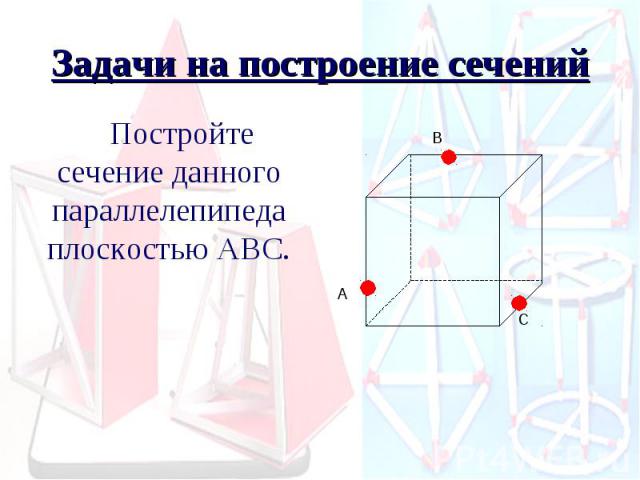
Задачи на построение сечений Постройте сечение данного параллелепипеда плоскостью АВС.