Презентация на тему: Понятие модуля числа

Формирование понятия модуля и умения выполнять действия с ними.

Определить значимость темы «Модуль» в математике. Определить значимость темы «Модуль» в математике. Углубить теоретические знания по решению упражнений с модулем; Оформление пособия исследовательской деятельности при решении задач с модулями; Составить пособие нестандартных задач с модулями.

1-й погружение в проект; 2-й организация деятельности; 3-й выпуск пособия «Решение упражнений с модулем »; 4-й презентация результатов

Тема: «Модуль числа» Предмет: математика Класс: 7 - 8 Тип проекта:  монопредметный, практико - ориентированный Форма работы: внеурочная

1. Развивать умение исследовать, проектировать в процессе анализа решения уравнения или неравенства с модулем; 1. Развивать умение исследовать, проектировать в процессе анализа решения уравнения или неравенства с модулем; Развивать умение работать с информационными технологиями. 2. Выпустить пособие для школьников.

Основывается на интересе учащихся к данной теме, и их желании получить знания по теме «Модуль», умений решать уравнения и неравенства с модулем. Основывается на интересе учащихся к данной теме, и их желании получить знания по теме «Модуль», умений решать уравнения и неравенства с модулем. Подготовка к ГИА.

1 – подбор литературы ,введение, определении значимости модуля; 1 – подбор литературы ,введение, определении значимости модуля; 2– способы решения уравнений и неравенств с модулем, выпуск пособия; 3 – оформление материала, презетация.

1. При работе с проектом использовался компьютер, дополнительная литература, услуги Интернета, подготовлены схемы решения уравнений и неравенств ; 1. При работе с проектом использовался компьютер, дополнительная литература, услуги Интернета, подготовлены схемы решения уравнений и неравенств ; 2. Решение уравнения: а) график функции; б) умения работать с дополнительной литературой; в) умения проводить аналогию.

Развитие: Развитие: - самостоятельной работы с источниками информации; - умения решать упражнения с модулем - самостоятельности в принятии решений - коммуникативности; - проектирования, планирования, анализа.

Главной целью этого проекта является расширение и углубление знаний, развитие интереса к предмету, развитие математических способностей. Главной целью этого проекта является расширение и углубление знаний, развитие интереса к предмету, развитие математических способностей.

Большую роль в развитии математического мышления играет изучение темы «Модуль числа». Большую роль в развитии математического мышления играет изучение темы «Модуль числа». Вместе с тем изучению этой темы в школьной программе не уделено достаточно внимания, в 6 и 7 классах изучаются самые азы понятия модуля и действия с ними. Интерес к теме объясняется тем, что уравнения с модулем предлагаются на школьных экзаменах (на ГИА и ЕГЭ).

Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово , которое имеет множество значений и применяется не только в математике,  но и в физике, технике, программировании и других точных науках. В технике – это термин служит для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости. В физике - это модуль объемного сжатия, отношение нормального напряжения в материале к относительному удлинению.

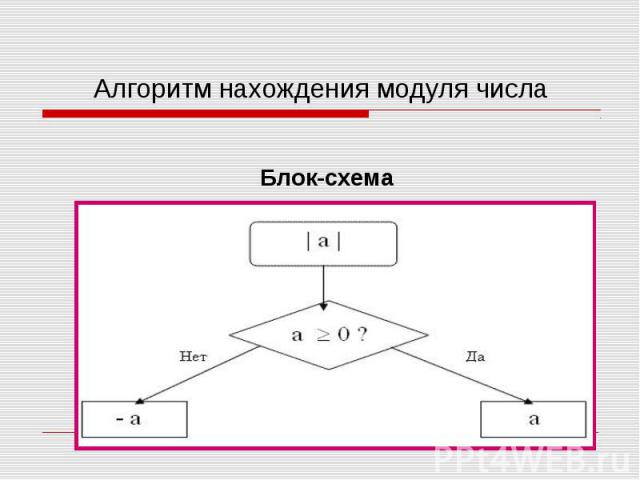
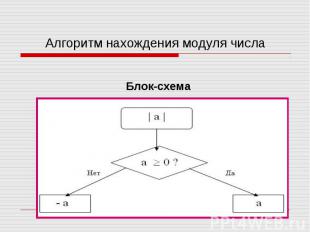
Уравнение – это равенство, содержащее переменные. Уравнение – это равенство, содержащее переменные. Уравнение с модулем – это уравнение, содержащее переменную под знаком абсолютной величины (под знаком модуля). Например:  | х | = 1 Решить уравнение – это значит найти все его корни, или доказать, что корней нет. Модуль – расстояние от начала отсчета до точки на числовой прямой.

Модуль – это расстояние от начала отсчета до точки на числовой прямой. Модуль – это расстояние от начала отсчета до точки на числовой прямой. А это значит: Модуль числа а равен а, если а больше или равно нулю и равен –а, если а меньше нуля:                            а, если  а > 0;               | а |=                         - а, если  а < 0. Из определения следует, что для любого действительного числа а,   | а | > 0 и | -а |  =  | а |.

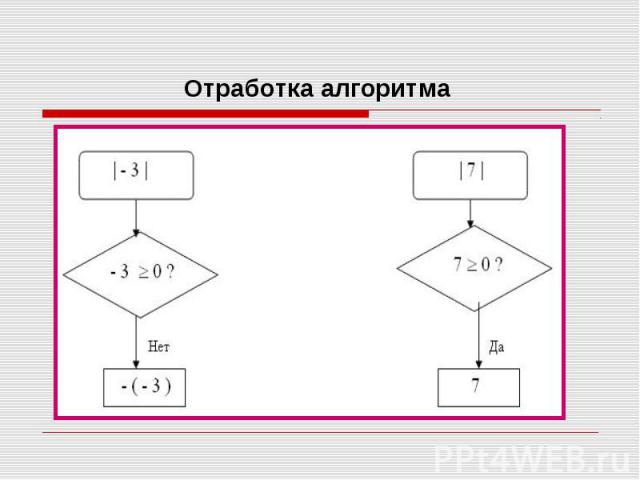
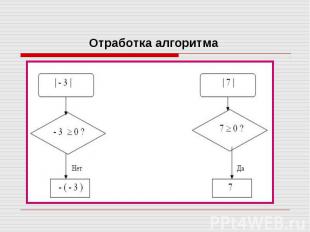
│5│= 5 │5│= 5 │2- 6│= - (- 4)=4 так как (2-6) – число отрицательное. │-8│= -(- 8 )= 8 так как (-8) – число отрицательное. │2-13│= -(-11)=11, так как (2-13) – число отрицательное.

׀х׀ = а х = а, если а>0 или х = -а, если а<0 ׀х׀ = а х = а, если а>0 или х = -а, если а<0 ׀х - 5׀=6 х-5=6 х=11, х-5=-6 х=-1 ׀2х+7׀=-4 ø решений нет. ׀ 7х-49׀=0 7х-49=0 7х=49 х=49:7 х=7

И в заключении я хотел бы сказать, что для досконального  изучения материала исследовательская работа подходит лучше всего. Мне представилась возможность больше поработать с интересной, для меня, темой модуля и выйти за рамки того материала, который предоставляет нам учебник 7-го класса. Прочитав и изучив другую литературу, я узнал много нового и, как я считаю, важного для меня. И в заключении я хотел бы сказать, что для досконального  изучения материала исследовательская работа подходит лучше всего. Мне представилась возможность больше поработать с интересной, для меня, темой модуля и выйти за рамки того материала, который предоставляет нам учебник 7-го класса. Прочитав и изучив другую литературу, я узнал много нового и, как я считаю, важного для меня.

Большое место в математике отведено решение упражнений по теме « Модуль числа». Интерес к теме объясняется тем, что уравнения с модулем предлагаются на школьных экзаменах и при подготовке к ГИА . Большое место в математике отведено решение упражнений по теме « Модуль числа». Интерес к теме объясняется тем, что уравнения с модулем предлагаются на школьных экзаменах и при подготовке к ГИА . С этой целью я подготовил методический сборник для углубленного изучения этого вопроса.

Мои умения работать с компьютерной техникой; Мои умения работать с компьютерной техникой; Мои умения исследовательской работы; Изучение темы «Модуль» и выход за рамки школьного материала; Выпуск пособие по математике для учащихся 7 – 8 классов ,который поможет им при подготовке к ГИА.

   

1 Найти значения выражений (приготовить карточки): |-100| , |5+1,1| , |4,4- 8,9| , -|-9,7| , |5-16| 1 Найти значения выражений (приготовить карточки): |-100| , |5+1,1| , |4,4- 8,9| , -|-9,7| , |5-16| 1 Найдите модуль числа _ 18 10 _ 16 9 2 4 2 Найдите положительное число модуль которого равен: 3 ; 5. 3. Известно,что |a|= 4 Чему равен |-a|? |a|= 4,6 Чему равен |-a|? |a|= 3,03 Чему равен |-a|? 4. Выберите из двух чисел, модуль которого меньше: -5 и 6 2 и -4 -2 и -3 5 Найдите значение выражения: |0,4| * |-2,5| |-40| * |0,1| |3,6| : |-1,2|

   

4. Заполни таблицу: 4. Заполни таблицу:  самопроверка по образцу: за 1–2 ошибки – оценка “4”, если нет ошибок – оценка “5”. 5. Сравните: а) | – 8 | и | – 5 | б) | 12,3 | и |-11 | в) | 0 | и | –| 1,5 |

Решите уравнение Решите уравнение а) | х | = 2,5 б) | х | = 0 в) | х | = – 4 г) | а | + 9 = 9 д) | в | – 3 = 33 е) 12,5 – | а | = 10,3 Отметьте на координатной прямой точки, изображающие числа: а) модуль которых равен 7; б) модуль которых меньше 7; в) модуль которых больше 7.

|5х + 3| = 1 |5х + 3| = 1 |2х - 3| = 1 |х - 5| + |2х –6| = 7 |х² + 3х| – |4 – х| = |х ²- х| 1 ≤ |2х – 1| ≤ 2 х² - 5|х| – 4 ≥ 0 |2х + 5| + |2х – 3| = 8 |х² + 2х| – |2 – х| = |х ²- х| 1 ≤ |3х – 2| ≤ 2 х² - 2|х| – 8 ≥ 0 |(3х + 1)(х – 3)| ≤ 3

Решить уравнения и неравенства Решить уравнения и неравенства |x|² - 4 = 0 | x|² - 4 < 0 3) |x|² - 4 > 0 |x|² - 3|x| ≥ 0 |x|² - 3|x| > 0 |x|² - 3|x| ≤ 0 |x|² - 3|x| < 0 В. x² - 2x + | x| = 0 x² - 2x + | x| < 0 x² - 2x + | x| > 0 |x² - 2x| + x = 0 |x² - 2x| + x < 0

Все слова можно отгадать, если вдумчиво и внимательно читать рисунок Все слова можно отгадать, если вдумчиво и внимательно читать рисунок

Под простейшими функциями понимают алгебраическую сумму модулей линейных выражений. Сформулируем утверждение, позволяющее строить графики таких функций, не раскрывая модули ( что особенно важно, когда модулей достаточно много ): "Алгебраическая сумма модулей n линейных выражений представляет собой кусочно- линейную функцию, график которой состоит из n +1 прямолинейного отрезка. Тогда график может быть построен по n +2 точкам, n из которых представляют собой корни внутримодульных выражений, ещё одна -- произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя с абсциссой, большей большего из корней. Под простейшими функциями понимают алгебраическую сумму модулей линейных выражений. Сформулируем утверждение, позволяющее строить графики таких функций, не раскрывая модули ( что особенно важно, когда модулей достаточно много ): "Алгебраическая сумма модулей n линейных выражений представляет собой кусочно- линейную функцию, график которой состоит из n +1 прямолинейного отрезка. Тогда график может быть построен по n +2 точкам, n из которых представляют собой корни внутримодульных выражений, ещё одна -- произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя с абсциссой, большей большего из корней.

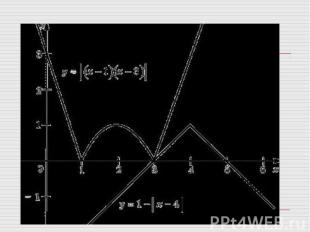
Построим графики функций y = |(x–1)(x–3)| и y=1–|x–4 | Построим графики функций y = |(x–1)(x–3)| и y=1–|x–4 | 1)в y = |(x–1)(x–3)| подставим значен дем пересечение с осью ОХ, для этого решим простое уравнение: 1-|x-4|=0 |x-4|=1 x - 4=1 или x - 4=-1 x=5 x=3 Следовательно данный график пересекает ось ОХ в точках 5 и 3. При х=4 у=1 и ак видно из графика: графики обеих функций пересекаются в одной точке 3 Ответ: 3

|x – 1| + |x – 2|=1 |x – 1| + |x – 2|=1 с использованием геометрической интерпритации модуля. Будем рассуждать следующим образом: исходя из геометрической интерпритации модуля, левая часть уравнения представляет собой сумму расстояний от некторой точки абсцисс х до двух фиксированных точек с абсциссами 1 и 2. Тогда очевидно, что все точки с абсциссами из отрезка [1; 2] обладают требуемым свойством, а точки, расположенные вне этого отрезка- нет. Отсюда ответ: множеством решений уравнения является отрезок [1; 2]. Ответ: х [1; 2]

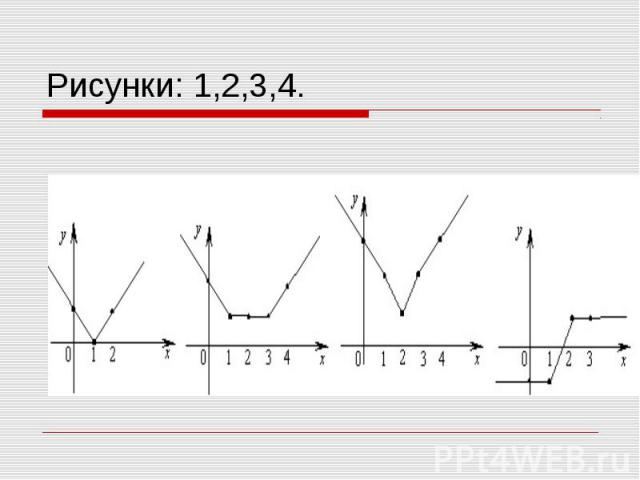
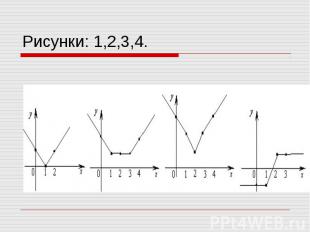
1) f(x)=|x - 1| Вычисляя функции в точках 1, 0 и 2, получаем график, состоящий из двух отрезков(рис.1) 1) f(x)=|x - 1| Вычисляя функции в точках 1, 0 и 2, получаем график, состоящий из двух отрезков(рис.1) 2) f(x)=|x - 1| + |x – 2| Вычисляя значение функиции в точках с абсциссами 1, 2, 0 и 3, получаем график, состоящий из двух отрезков прямых.(рис.2) 3) f(x)=|x - 1| + |x – 2| + |x – 3| Для построения графика вычислим значения функции в точках 1, 2, 3, 0 и 4 (рис.3) 4) f(x)=|x - 1| - |x – 2| График разности строится аналогично графику суммы, то есть по точкам 1, 2, 0 и 3. См. рис1,2,3,4.

у = |x² - 5x + 6| = 0 |(x - 2)² - 3| = 0 |x² - 3| = 0 у = |x² - 7x + 10| = 0 |(x + 2)² - 4| = 0 |x² + 5| = 0