Презентация на тему: Функция
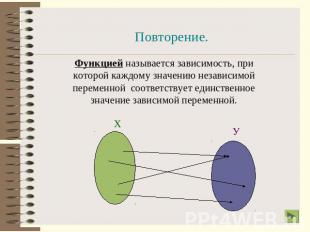
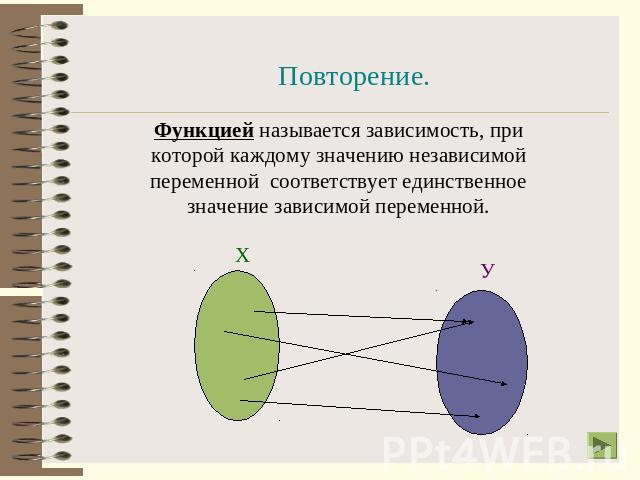
Повторение.Функцией называется зависимость, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.
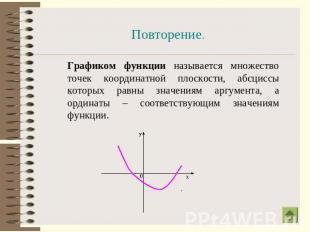
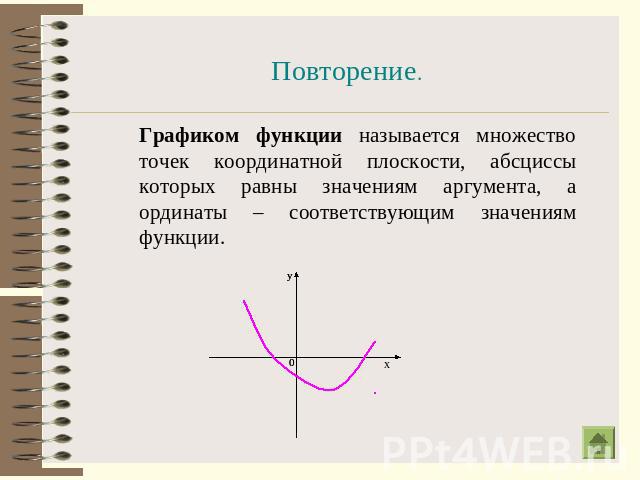
Повторение. Графиком функции называется множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.

Определение. Линейной функцией называется функция, которую можно задать формулой y = kx + b, где x - независимая переменная, k и b - некоторые числа. Графиком линейной функции является прямая.
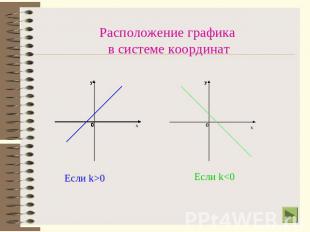
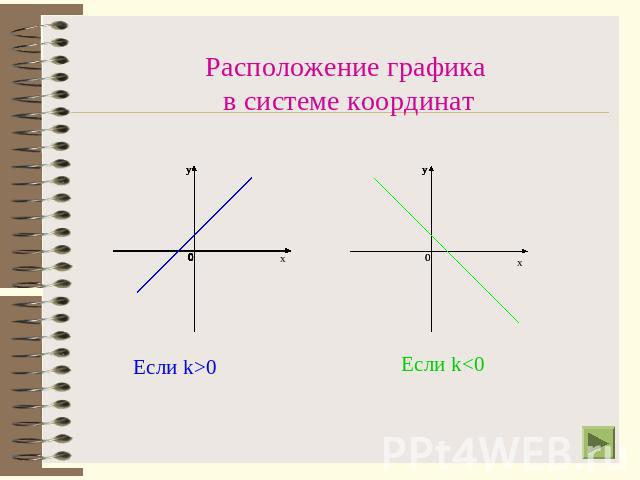
Расположение графика в системе координат

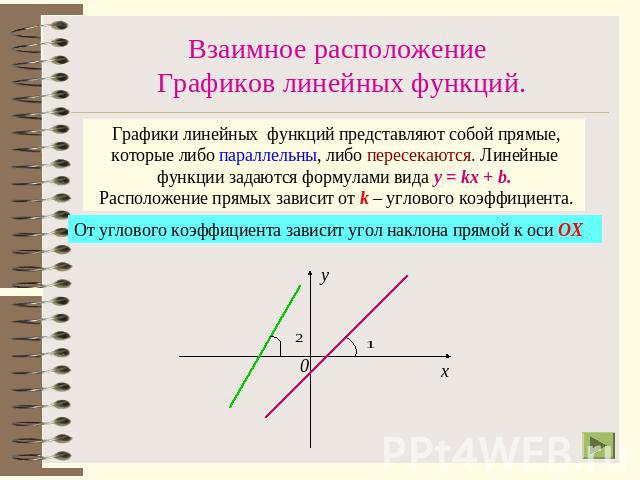
Взаимное расположение Графиков линейных функций. Графики линейных функций представляют собой прямые, которые либо параллельны, либо пересекаются. Линейные функции задаются формулами вида у = kх + b. Расположение прямых зависит от k – углового коэффициента.От углового коэффициента зависит угол наклона прямой к оси ОХ
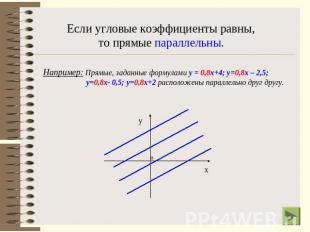
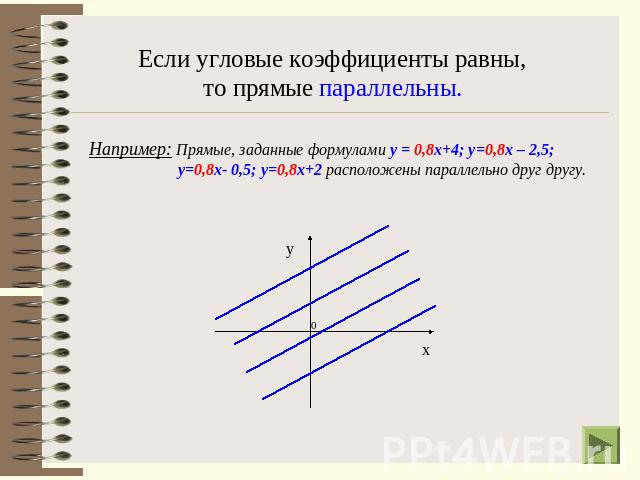
Если угловые коэффициенты равны, то прямые параллельны.Например: Прямые, заданные формулами у = 0,8х+4; у=0,8х – 2,5; у=0,8х- 0,5; у=0,8х+2 расположены параллельно друг другу.
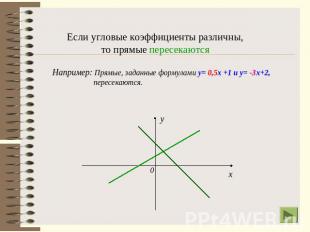
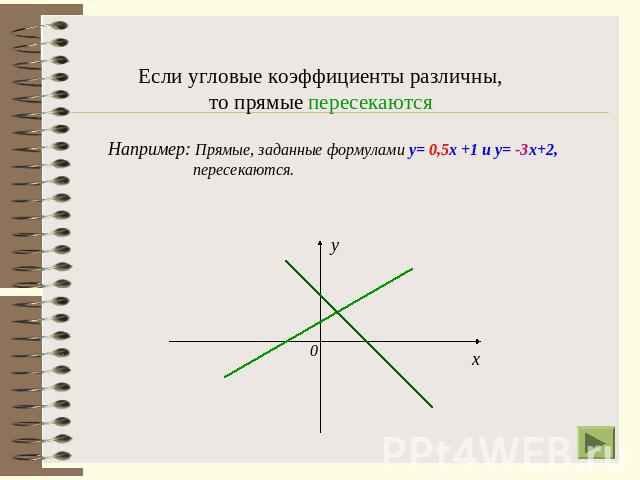
Если угловые коэффициенты различны,то прямые пересекаютсяНапример: Прямые, заданные формулами у= 0,5х +1 и у= -3х+2, пересекаются.

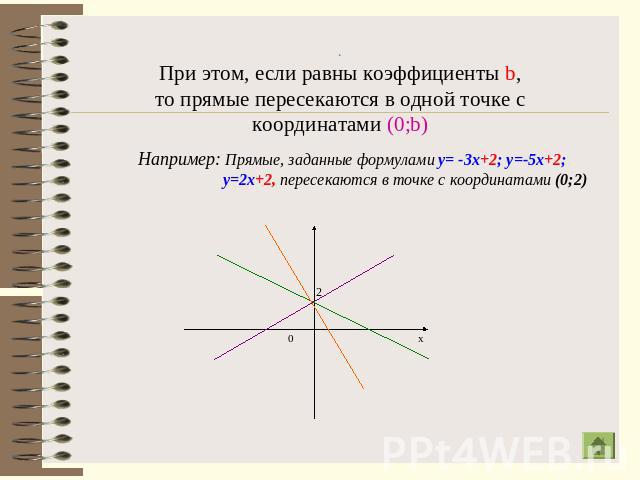
.При этом, если равны коэффициенты b,то прямые пересекаются в одной точке с координатами (0;b)Например: Прямые, заданные формулами у= -3х+2; у=-5х+2; у=2х+2, пересекаются в точке с координатами (0;2)

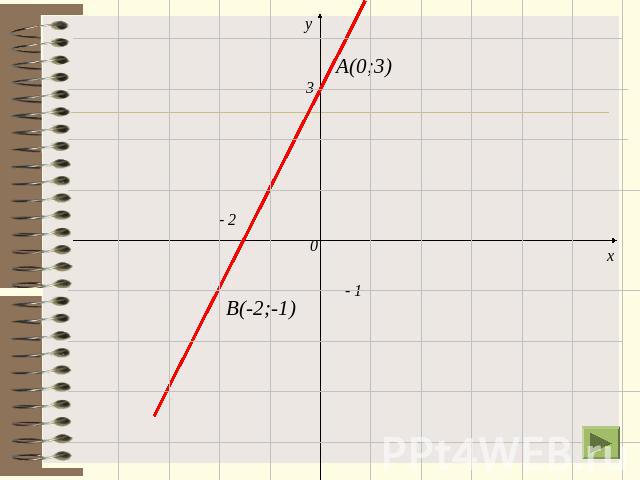
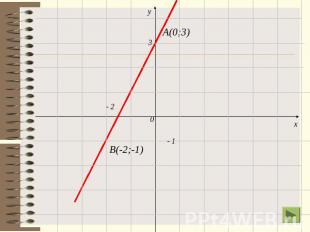
Построение графика линейной функцДля построения графика линейной функции достаточно найти координаты двух точек графика, отметить эти точки в координатной плоскости и провести через них прямую.и.Пример. Построить график функции у= 2х+3. Используя формулу у=2х+3, найдем координаты двух точек графика.:если х=0 то у=2 0+3= 3,если х= -2, то у= 2 (-2)+3= -1.Отметим точки А(0;3) и В(-2;1). Проведем через эти точки прямую.
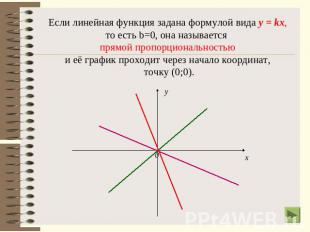
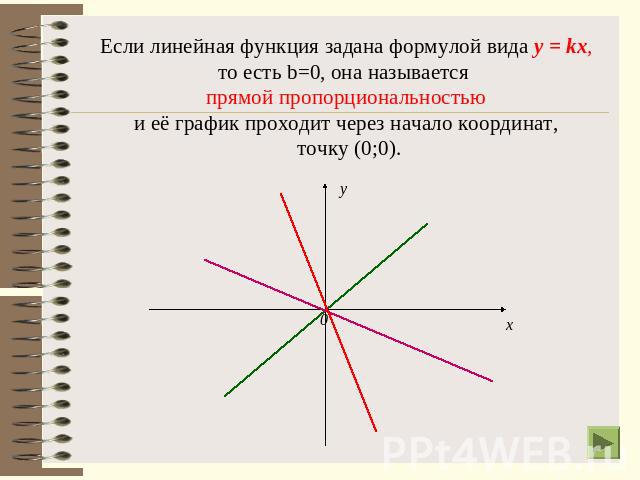
Если линейная функция задана формулой вида у = kх,то есть b=0, она называется прямой пропорциональностьюи её график проходит через начало координат, точку (0;0).

Если линейная функция задана формулой у = b, то есть k=0,то её график проходит через точку с координатами (b;0)параллельно оси ОХ.Например: Прямые, заданные формулами у = 4; у= - 3; у = 1 расположены следующим образом: