Презентация на тему: Функция тангенса

Автор: учитель высшей категории Стрелкова Н. В. (Алгебра-11) 5klass.net

Цели урока: повторить раннее изученные свойства функции у=tgx; научиться строить график функции у=tgx, используя данные свойства функции. на основе анализа графика определить остальные свойства функции научиться решать простейшие уравнения и неравенства с помощью графика функции.

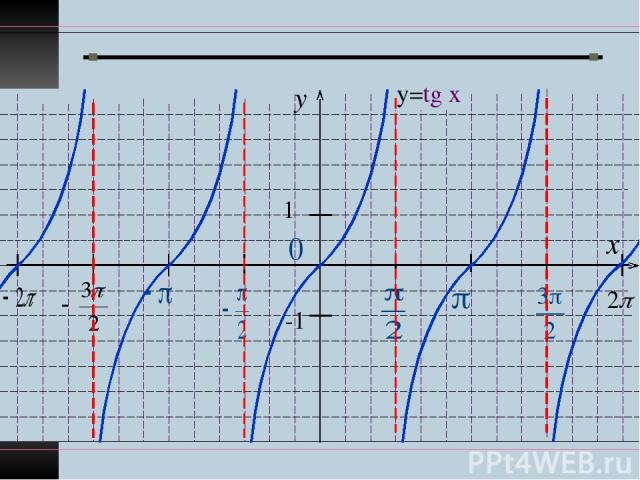
Функция y=tg x и её свойства. 1. Обл. определения: . 2. Множество значений функции: уєR. 3. Периодическая, Т= π. 4. Нечётная функция. хє[0;π/2)

Функция y=tg x возрастает на промежутке 2. Т. к. функция у=sin x возрастает на данном промежутке, то sin х1< sin x2. 3. Т. к. функция у=соs x убывает на данном промежутке, то соs х1> соs x2 и (1) (2) 4.Умножим нер-во (1) на нер-во (2) : , т. е. tg x1< tg x2 .

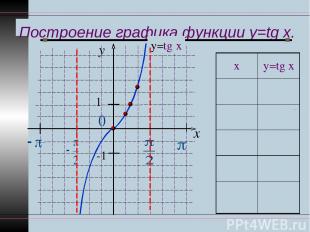
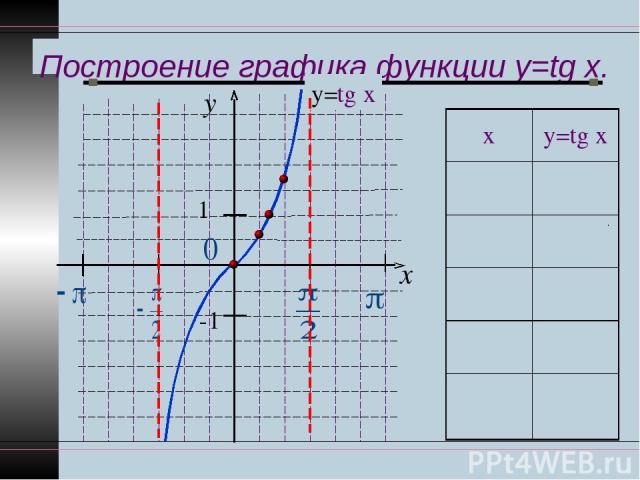
Построение графика функции y=tg x. y x 1 -1 у=tg x х у=tg x 0 0 π ∕6 1 ∕ 3 π ∕4 1 π ∕3 3 π ∕2 Не сущ.

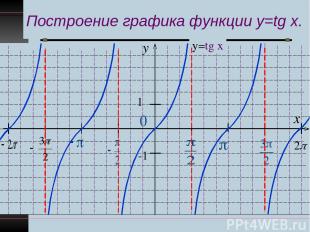
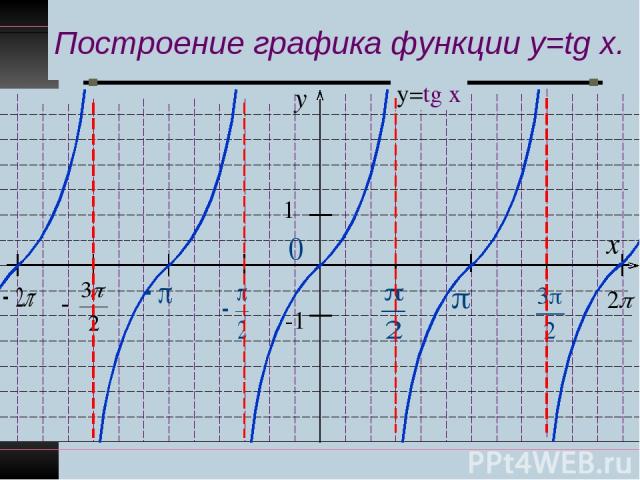
Построение графика функции y=tg x. y x 1 -1 у=tg x

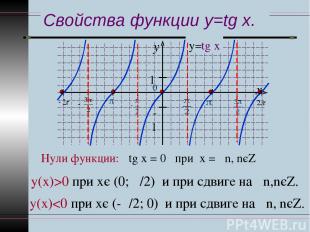
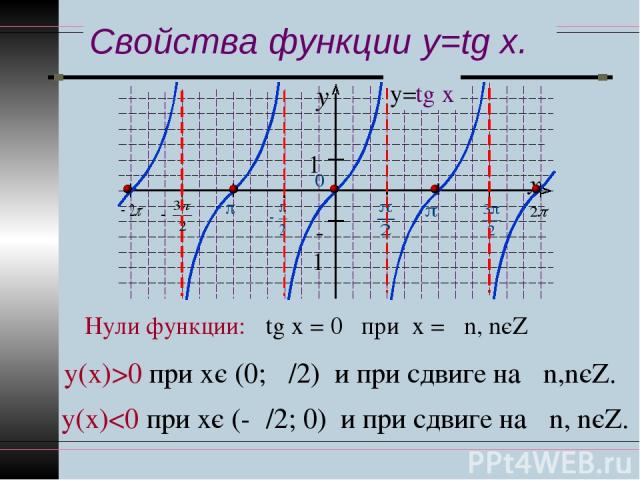
Свойства функции y=tg x. Нули функции: tg х = 0 при х = πn, nєZ у(х)>0 при хє (0; π/2) и при сдвиге на πn,nєZ. у(х)

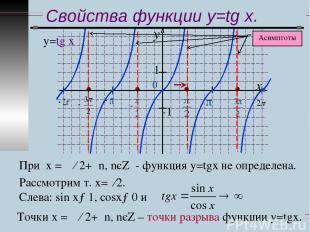
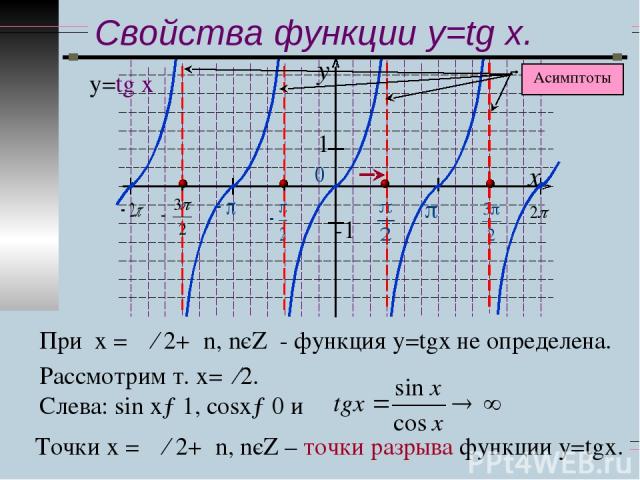
Свойства функции y=tg x. у=tg x При х = π ∕ 2+πn, nєZ - функция у=tgx не определена. Рассмотрим т. х=π∕2. Слева: sіn x→1, сosx→0 и Точки х = π ∕ 2+πn, nєZ – точки разрыва функции у=tgx.

Свойства функции y=tgx. 1. Обл. определения: . 2. Множество значений функции: уєR. 3. Периодическая, Т= π. 4. Нечётная функция. 5. Возрастает на всей области определения. 6. Нули функции у (х) = 0 при х = πn, nєZ. 7. у(х)>0 при хє (0; π/2) и при сдвиге на πn,nєZ. 8. у(х)

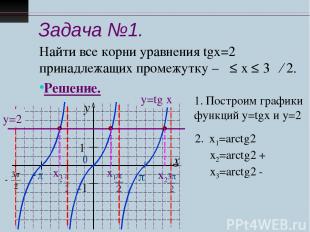
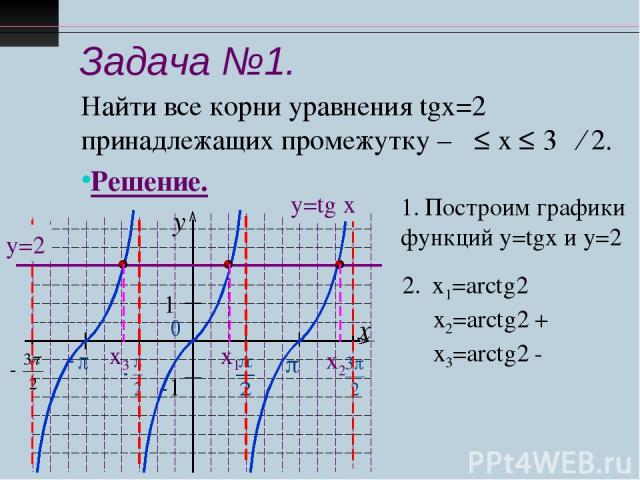
Задача №1. Найти все корни уравнения tgx=2 принадлежащих промежутку –π ≤ х ≤ 3π ∕ 2. Решение. у=tg x у=2 Построим графики функций у=tgx и у=2 х1=arctg2 х2=arctg2 + π х3=arctg2 - π х1 х3 х2

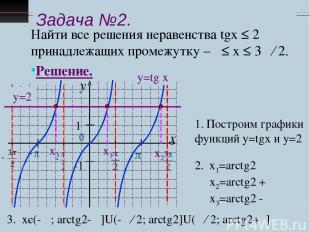
Задача №2. Найти все решения неравенства tgx ≤ 2 принадлежащих промежутку –π ≤ х ≤ 3π ∕ 2. Решение. у=tg x у=2 Построим графики функций у=tgx и у=2 х1=arctg2 х2=arctg2 + π х3=arctg2 - π х1 х3 х2 3. хє(-π ; arctg2- π]U(-π ∕ 2; arctg2]U(π ∕ 2; arctg2+π]

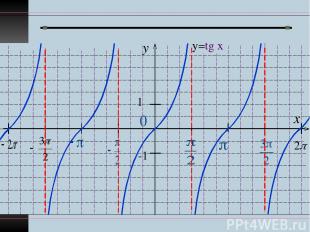
y x 1 -1 у=tg x