Презентация на тему: Франсуа Виет и его теорема

Франсуа Виет и его теорема как инструмент для решения уравнений 900igr.net

Франсуа Виет (1540-1603) В 2010 году исполнилось 470 лет со дня рождения замечательного французского математика, положившего начало алгебре как науке о преобразовании выражений, создателя буквенного исчисления, Франсуа Виета.

Актуальность Уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее число задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Уравнения решали двадцать пять веков назад. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня.

Цель: изучить материал о великом учёном, французском математике – Франсуа Виете, рассмотреть квадратные уравнения частного порядка, научиться использовать теорему Виета как инструмент для решения уравнений и задач, связанных с корнями и коэффициентами уравнения n-ой степени.

Задачи: выяснить из различных источников кто такой Франсуа Виет, его вклад в математику; узнать историю его жизни; повторить понятие квадратного уравнения, узнать об уравнениях частного порядка и их решении рациональным способом; узнать какие уравнения называются уравнениями высших степеней; рассмотреть теорему Виета как инструмент для решения уравнений и других задач.

Кто Вы, господин Виет? Франсуа Виет – крупнейший французский математик 16 века Родился в 1540 году во Франции в городе Фонтене-ле-Конт. По образованию юрист. Но все свое свободное время он отдавал занятиям математикой, а также астрономией. Особенно увлеченно он начал работать в области математики с 1584г. Виет детально изучил труды, как древних, так и современных ему математиков. Разработал почти всю элементарную алгебру. Известны «формулы Виета», дающие зависимость между корнями и коэффициентами алгебраического уравнения. Ввел буквенные обозначения для коэффициентов в уравнениях.

Главные открытия Ф. Виета изложены в знаменитом «Введении в аналитическое искусство», опубликованном в 1591 году. Основной замысел ученого замечательно удался: началось преобразование алгебры в мощное математическое исчисление. Франсуа называл алгебру аналитическим искусством. Он писал в письме к де Партене: «Все математики знали, что под алгеброй скрыты несравненные сокровища, но не умели их найти…» Математические открытия

Интересные факты из жизни и деятельности ученого Франсуа Виет, вычисляя периметры вписанного и описанного 322 216-угольников, получил 9 точных десятичных знаков. Впервые обозначать десятичные дроби с помощью запятой предложил Франсуа Виет. До него изображение дробей было весьма сложным. Так, например, дробь 0,3469 писалась так: 3(1)4(2)6(3)9(4). Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым он внедрил в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т.е. ввести понятие математической формулы. Ученый мог работать по трое суток без сна!

Теорему Виета можно обобщить на многочлены любой степени. Непосредственно применение трудов Виета очень затруднялось тяжелым и громоздким изложением. Из-за этого они полностью не изданы до сих пор. Г.Г. Цейтен отмечал, что чтение работ Виета затрудняется несколько изысканной формой, в которой повсюду сквозит его большая эрудиция, и большим количеством изобретенных им и совершенно не привившихся греческих терминов. Потому влияние его, столь значительное по отношению ко всей последующей математике, распространялось сравнительно медленно. Виет первым стал применять скобки, которые, правда, у него имели вид не скобок, а черты над многочленом.

Квадратные уравнения Квадратным уравнением называют уравнения вида ax²+bx+c = 0, где коэффициенты a, b, c – любые действительные числа, причём a ≠ 0. Квадратное уравнение называют приведённым, если его старший коэффициент равен 1. Пример: x2 + 2x + 6 = 0. Квадратное уравнение называют не приведенным, если старший коэффициент отличен от 1. Пример: 2x2 + 8x + 3 = 0. Полное квадратное уравнение - квадратное уравнение, в котором присутствуют все три слагаемых, иными словами, это уравнение, у которого коэффициенты b и c отличны от нуля.

Теорема Виета Очень любопытное свойство корней квадратного уравнения обнаружил французский математик Франсуа Виет. Это свойство назвали теорема Виета: Чтобы числа x1 и x2 являлись корнями уравнения: ax² + bx + c = 0 необходимо и достаточно выполнения равенства x1 + x2 = -b/a и x1x2 = c/a Пример. х²-4х-12=0 х1=-2 х2=6

По праву в стихах быть воспета О свойствах корней теорема Виета. Что лучше, скажи, постоянства такого: Умножишь ты корни и дробь уж готова: В числителе С, в знаменателе А, А сумма корней тоже дроби равна Хоть с минусом дробь эта, что за беда- В числителе B, в знаменателе A. И. Дырченко

Квадратные уравнения частного характера 1) Если a + b + c = 0 в уравнении ax² + bx + c = 0, то х1=1, а х2 = 2)Если a - b + c = 0, в уравнении ax² + bx + c= 0, то: х1=-1, а х2 =- 3) Метод “переброски” Корни квадратных уравнений y² + by + аc = 0 и ax² + bx + c = 0 связанны соотношениями: х1 = и х2 =

Пример 418х² - 1254х + 836 = 0 Этот пример очень тяжело решить через дискриминант, но, зная выше приведенную формулу его с легкостью можно решить. a = 418, b = -1254, c = 836. х1 = 1, х2 = 2

Формула Виета для многочленов (уравнений) высших степеней   Формулы, выведенные Виетом для квадратных уравнений, верны и для многочленов высших степеней. Пусть многочлен P(x) = a0xn + a1xn-1 + … +an имеет n различных корней x1 , x2 …, xn. В этом случае он имеет разложение на множители вида: a0xn + a1xn-1 +…+ an = a0( x – x1)( x – x2)*…*(x – xn) Разделим обе части этого равенства на a0 ≠ 0 и раскроем в первой части скобки. Получим равенство:   xn + ( )xn-1 + … + ( ) = xn – (x1 + x2 + … + xn) xn-1 + ( x1x2 + x2x3 + … + xn-1xn)xn-2 + … +(-1)n x1x2 … xn

Но два многочлена тождественно равны в том и только в том случае, когда коэффициенты при одинаковых степенях равны. Отсюда следует, что выполняется равенство x1 + x2 + … + xn = - x1x2 + x2x3 + … + xn-1xn = x1x2 … xn = (-1)n Например, для многочленов третей степени a0x³ + a1x² + a2x + a3 имеем тождества x1 + x2 + x3 = - x1x2 + x1x3 + x2x3 = x1x2x3 = -

Если старший коэффициент многочлена , то для применения формул Виета нужно разделить все коэффициенты на . В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.

Обратные корни Напишем приведённое кубическое уравнение , корни которого обратны корням уравнения Решение: 1) Пусть - корни уравнения 2) Т.к. , то по формулам Виета

3) Пусть - корни уравнения 4) Тогда , , 5) Т.к. , то по формулам Виета 6) Следовательно искомое уравнение имеет вид: , или .

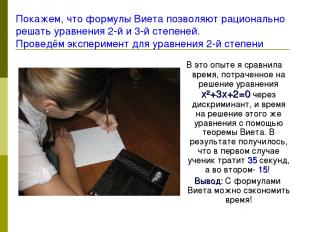
Покажем, что формулы Виета позволяют рационально решать уравнения 2-й и 3-й степеней. Проведём эксперимент для уравнения 2-й степени В это опыте я сравнила время, потраченное на решение уравнения x²+3x+2=0 через дискриминант, и время на решение этого же уравнения с помощью теоремы Виета. В результате получилось, что в первом случае ученик тратит 35 секунд, а во втором- 15! Вывод: С формулами Виета можно сэкономить время!

Проведём эксперимент для уравнения 3-й степени Дано уравнение: Ищем корень среди чисел: Подбором находим один из корней уравнения, - . Следовательно, делится на .

или По формулам Виета: Ответ:

Теперь решим то же уравнение с помощью формул Виета По формулам Виета: Следовательно, корни уравнения равны Вывод: формулы Виета позволяют рационально решить это уравнение.

При решении уравнений было замечено, что уравнения и имеют взаимно обратные корни.

Гипотеза Корни уравнений и , где , взаимно обратные.

Доказательство По формулам Виета из первого уравнения: Рассмотрим числа и

Значит, эти числа являются корнями уравнения что равносильно уравнению .

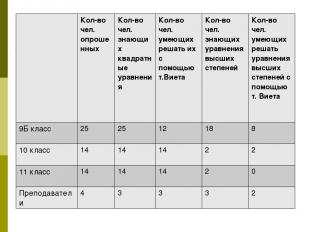
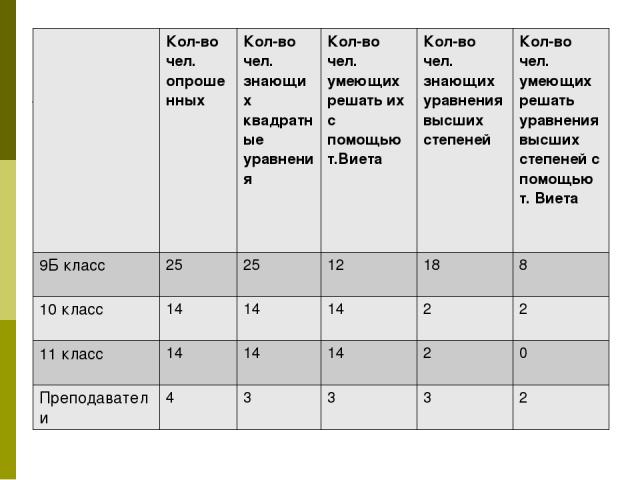
Кол-во чел. опрошенных Кол-во чел. знающих квадратные уравнения Кол-во чел. умеющих решать их с помощью т.Виета Кол-во чел. знающих уравнения высших степеней Кол-во чел. умеющих решать уравнения высших степеней с помощью т. Виета 9Б класс 25 25 12 18 8 10 класс 14 14 14 2 2 11 класс 14 14 14 2 0 Преподаватели 4 3 3 3 2

Спасибо за внимание!