Презентация на тему: Алгебра «Тригонометрические функции»

СПРАВОЧНИК по алгебре и началам анализа 10-11 классы 2009 г 900igr.net

Содержание. 1-3. Содержание 4. Числовая окружность. 5. Числовая окружность на координатной плоскости 6. Синус и косинус. 7. Тангенс и котангенс. 8. Тригонометрические функции числового аргумента 9. Тригонометрические функции углового аргумента 10. Формулы приведения. 11. Таблица значений тригонометрических функций некоторых углов. 12. Формулы преобразования тригонометрических функций. 13. Формулы преобразования произведения тригонометрических функций в сумму. 14. Формулы двойного угла. . Формулы понижения степени. 15. Формулы половинного аргумента. 16. Универсальная подстановка

Содержание 17. Преобразование сумм тригонометрических функций в произведения. 18. Формула дополнительного угла 19. Арксинус.Арккосинус. Арктангенс. Арккотангенс 20. Решение простейших тригонометрических уравнений 21. Однородные тригонометрические уравнения. 22. Решение однородных тригонометрических уравнений. 23. Введение вспомогательного угла. 24. Решение тригонометрических неравенств вида sin x > a, sin x < a. 25. Решение тригонометрических неравенств вида сos x > a, cos x < a. 26. Решение тригонометрических неравенств вида tg x > a, tg x < a. 27. Решение уравнений и неравенств. 28. Решение уравнений и неравенств . 29. Решение неравенств с помощью систем. 30. Решение неравенств с помощью систем.

Тригонометрия. Числовая окружность Дана единичная окружность, на ней отмечена начальная точка А — правый конец горизонтального диаметра. Поставим в соответствие каждому действительному числу t точку окружности по следующему правилу: 1) Если t > 0, то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь АМ длиной t. Точка М и будет искомой точкой М(t). 2) Если t < 0, то, двигаясь из точки А в направлении по часовой стрелке (отрицательное направление обхода окружности), опишем по окружности путь АМ длиной|t|.Точка М и будет искомой точкой М(t). 3) Числу t = 0 поставим в соответствие точку А; А = А(О). Единичную окружность с установленным соответствием (между действительными числами и точками окружности) будем называть числовой окружностью.

Синус и косинус Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют косинусом числа t и обозначают cos t, а ординату точки М называют синусом числа t и обозначают sin t. если М(t)=М(х; у), то x = cos t y = sin t

Тангенс и котангенс Отношение синуса числа t к косинусу того же числа называют тангенсом числа t и обозначают tg t. Отношение косинуса числа t косинусу того же числа называют котангенсом числа t и обозначают ctg t.

Тригонометрические функции числового аргумента.

Тригонометрические функции углового аргумента

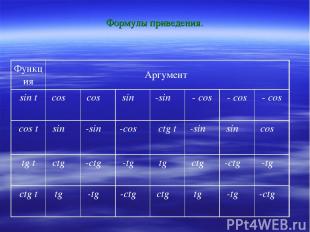
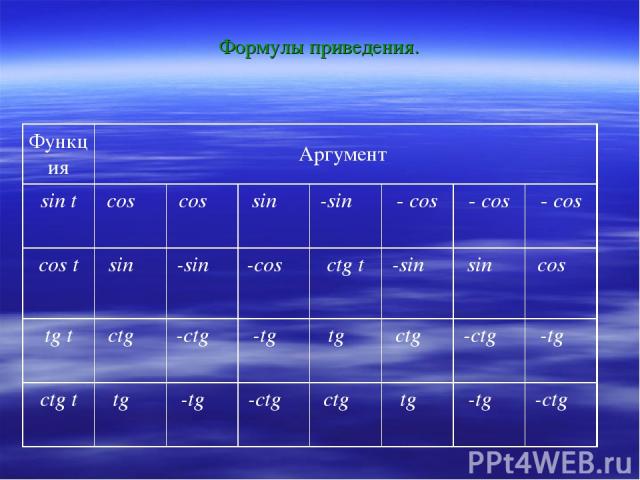
Формулы приведения. Функция Аргумент sin t cos α cos α sin α -sin α - cos α - cos α - cos α cos t sin α -sin α -cos α ctg t -sin α sin α cos α tg t ctg α -ctg α -tg α tg α ctg α -ctg α -tg α ctg t tg α -tg α -ctg α ctg α tg α -tg α -ctg α

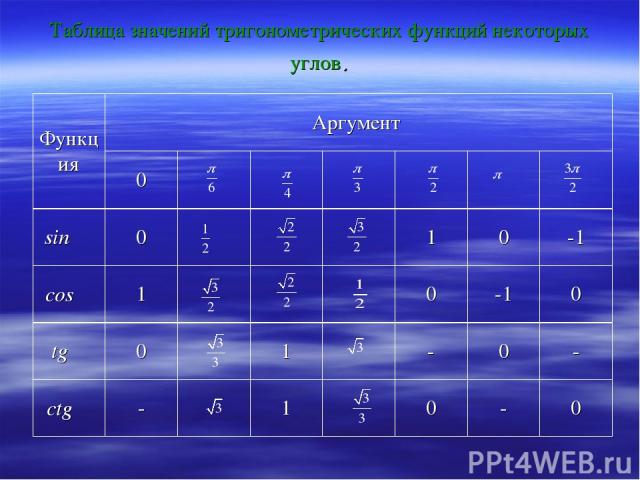
Таблица значений тригонометрических функций некоторых углов. Функция Аргумент 0 sin α 0 1 0 -1 cos α 1 0 -1 0 tg α 0 1 - 0 - ctg α - 1 0 - 0

Формулы преобразования тригонометрических функций

Формулы преобразования произведения тригонометрических функций в сумму.

Преобразование сумм тригонометрических функций в произведения.

Преобразование выражения А sin x + B cos x к виду C sin (x+t) Формула дополнительного угла

Тригонометрические функции числового аргумента. Арксинус. Арккосинус. Арктангенс. Арккотангенс

Решение простейших тригонометрических уравнений. Уравнение f (x) = а, где а данное число, а f(х) – одна из основных тригонометрических функций, называют простейшим тригонометрическим уравнением.

Однородные тригонометрические уравнения Уравнение вида a sin x + b cos x = 0 называют однородным тригонометрическим уравнением первой степени; уравнение вида a sin2 f (x) + bsin f (x) cos f ( x) + c cos 2 f (x)= 0 называют однородным тригонометрическим уравнением второй степени;

Решение однородных тригонометрических уравнений.

Решение тригонометрических уравнений. Введение вспомогательного угла.

Решение тригонометрических неравенств вида sin x > a, sin x < a. 1.Неравенства, содержащие переменную только под знаком тригонометрической функции, называют тригонометрическими. 2.При решении тригонометрических неравенств используют свойство монотонности тригонометрических функций, а также промежутки их знакопостоянства. 3.Для решения простейших тригонометрических неравенств вида sin x > a, (sin x < a.) используют единичную окружность или график функции у = sin x. 4. Важным моментом является знание ,что

Решение тригонометрических неравенств вида сos x > a, cos x < a. 1.Для решения простейших тригонометрических неравенств вида cos x > a, (cos x < a.) используют единичную окружность или график функции у = cos x. 2. Важным моментом является знание ,что

Решение тригонометрических неравенств вида tg x > a, tg x < a. 1.Для решения простейших тригонометрических неравенств вида tg x > a, (tg x < a.) используют единичную окружность или график функции у = tg x. 4. Важным моментом является знание ,что

Решение уравнений и неравенств

Решение уравнений и неравенств

Решение неравенств с помощью систем.

Решение неравенств с помощью систем.