Презентация на тему: Тригонометрические функции. Синус

Тригонометрические функции. Синус.Урок в 11 классе

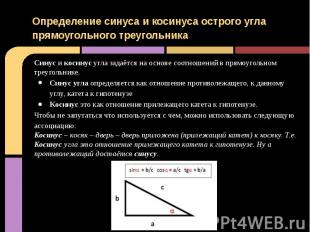
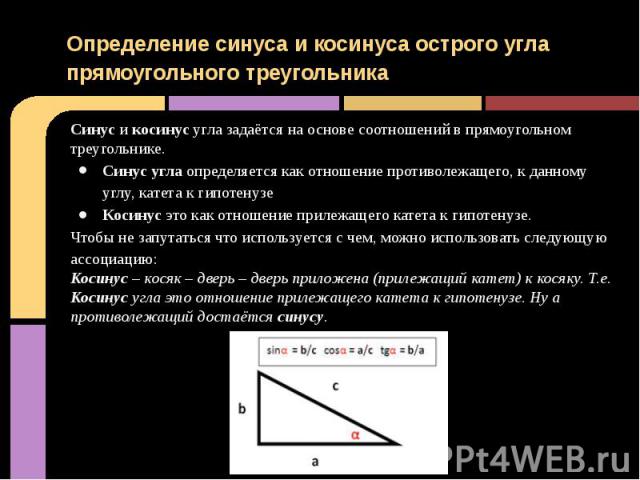
Определение синуса и косинусаОпределение синуса и косинуса острого угла прямоугольного треугольника Синус и косинус угла задаётся на основе соотношений в прямоугольном треугольнике.Синус угла определяется как отношение противолежащего, к данному углу, катета к гипотенузеКосинус это как отношение прилежащего катета к гипотенузе.Чтобы не запутаться что используется с чем, можно использовать следующую ассоциацию:Косинус – косяк – дверь – дверь приложена (прилежащий катет) к косяку. Т.е. Косинус угла это отношение прилежащего катета к гипотенузе. Ну а противолежащий достаётся синусу.

Вспомни синусы некоторых углов. Посмотри фильм.

Значения и знаки синуса и косинусаЗначения и знаки синуса и косинусаЗнаки синуса по четвертям Для нахождения значений и знака синуса на единичной окружности используется ордината или ось Y, косинуса – абсцисса или ось X. Для их запоминания используется следующая запоминалка: Синус - синий – синее небо. На синее небо, вверх, указывает ось Y. Значит ось X достаётся косинусу.

Областью определения функции синус является множество всех действительных чисел, т. е. D(y) = R. Каждому действительному числу х соответствует единственная точка единичной окружности Рx, получаемая поворотом точки Р0(1; 0) на угол, равный х радиан. Точка Рx имеет ординату, равную sinх. Следовательно, для любого х определено значение функции синус.

Свойства функции синус 2. Множеством значений функции синус является промежуток [-1; 1], т. е. Е(у) = [-1;1]Это следует из определения синуса: ордината любой точки единичной окружности удовлетворяет условию -1≤y≤1

3. Функция синус является нечетной, т. е. для любого x∈R выполняется равенство sin(-x)=-sinx Пусть точка Рx получена при повороте точки Р0 на x радиан, а точка Р-x получена при повороте точки Р0 на -х радиан.Треугольник ОРxР-x является равнобедренным; ON — биссектриса угла РxОР-x, значит, ON является медианой и высотой, проведенной к стороне РxР-x. Следовательно, PxN = Р-xN, т. е. ординаты точек Рx и Р-x одинаковы по модулю и противоположны по знаку. Это означает, что sin(-x) = -sinx.

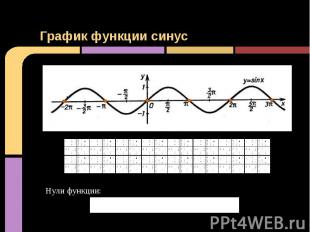
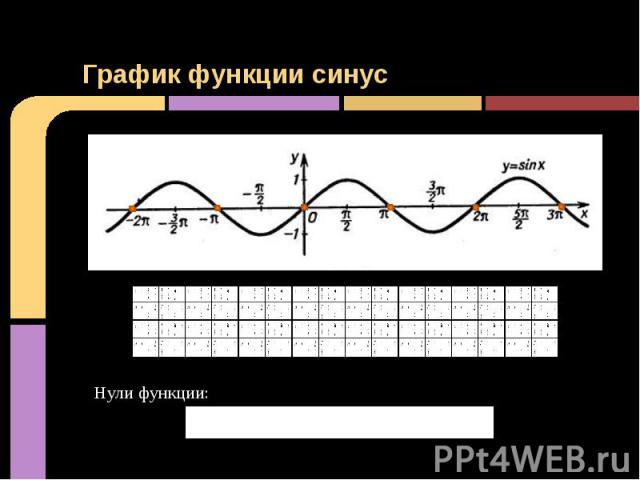
График функции синус Нули функции:

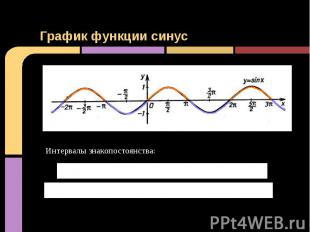
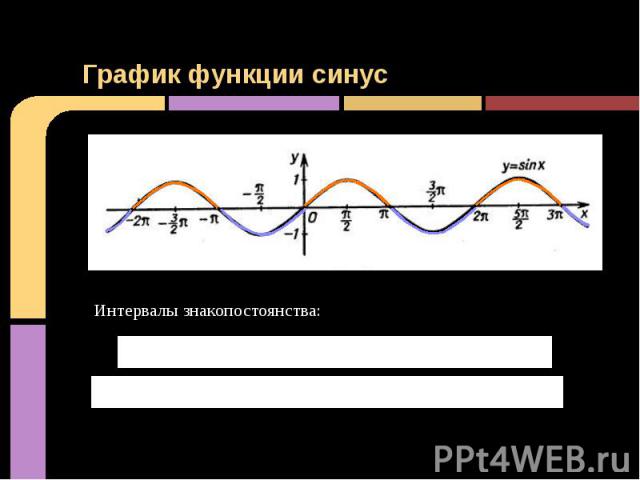
График функции синус Интервалы знакопостоянства:

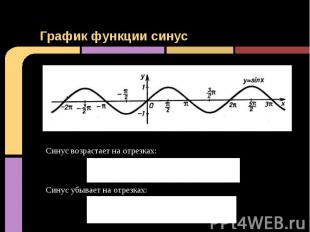
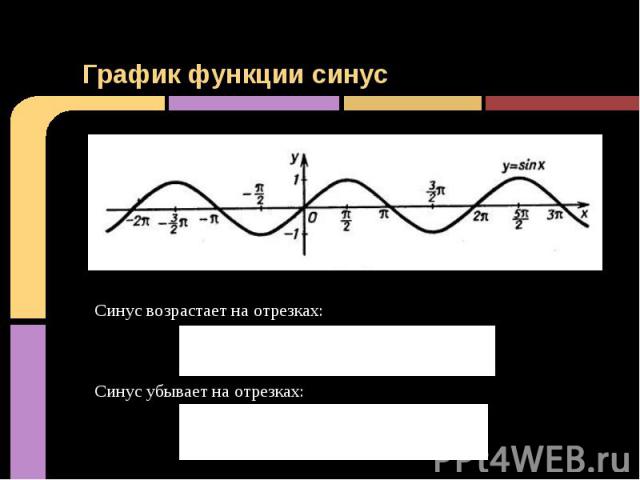
График функции синус Синус возрастает на отрезках: [−

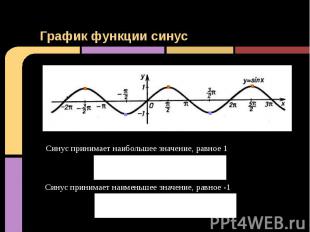
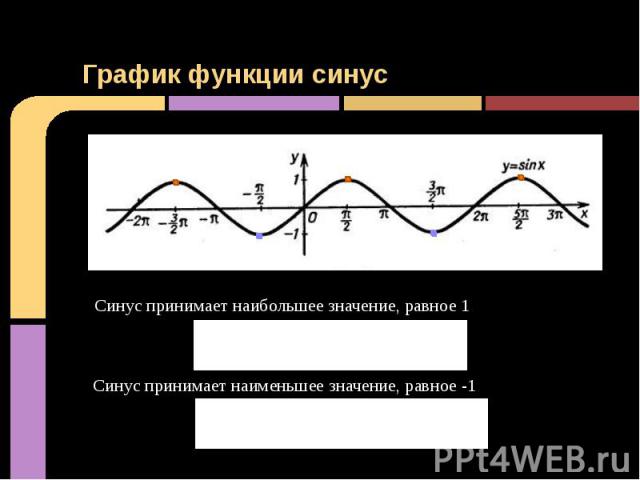
График функции синус Синус принимает наибольшее значение, равное 1 при