Презентация на тему: Повторение планиметрии

Повторение планиметрии Презентацию подготовилаучитель математикиСеребрянская Л. А.

Планиметрия — раздел геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Фигуры, изучаемые планиметрией: Точка Прямая Параллелограмм (частные случаи Квадрат, Прямоугольник, Ромб) Трапеция Окружность Треугольник Многоугольник

Точка — абстрактный объект в пространстве, обладающий координатами, но не имеющий размеров, массы, направленности и каких-либо других геометрических или физических характеристик. Одно из фундаментальных понятий в математике и физике. Прямая. Прямая линия — одно из основных понятий геометрии. При систематической изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.

Треугольник Треугольник — простейший многоугольник, имеющий 3 вершины и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки.

ТРЕУГОЛЬНИК АВ=a, ВС=b, АС =c– стороны треугольникаBH-высота

Параллелограмм Параллелограмм (от греч. parallelos — параллельный и gramme — линия) — это четырехугольник, у которого противолежащие стороны попарно параллельны, т. е. лежат на параллельных прямых. Частным случаем параллелограмма (являются прямоугольник и ромб.

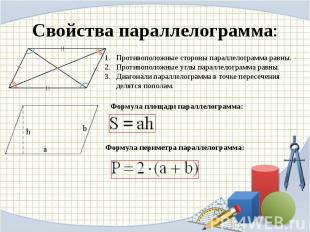
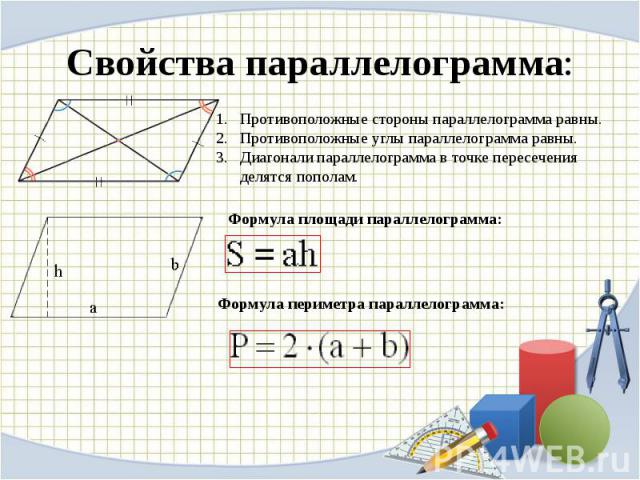
Свойства параллелограмма: Противоположные стороны параллелограмма равны.Противоположные углы параллелограмма равны.Диагонали параллелограмма в точке пересечения делятся пополам. Формула площади параллелограмма: Формула периметра параллелограмма:

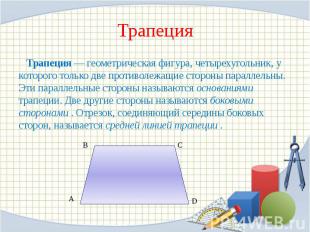
Трапеция Трапеция — геометрическая фигура, четырехугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами . Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

ТРАПЕЦИЯ Свойства сторон: Свойства средней линии: Площадь:

Окружность Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), лежащей в той же плоскости, что и кривая.

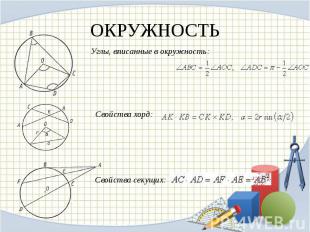
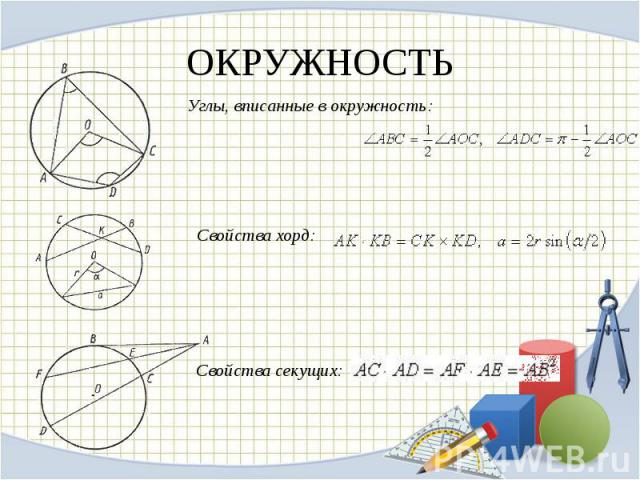
ОКРУЖНОСТЬ Углы, вписанные в окружность: Свойства хорд: Свойства секущих:

Длина окружности: Длина дуги в радиан: Длина дуги в : Площадь круга: Площадь сектора в радиан: Площадь сектора в : Площадь кругового сегмента, содержащего дугу в :

Многоугольник Многоугольник — это геометрическая фигура, обычно определяется как замкнутая ломаная без самопересечений, однако иногда самопересечения допускаются. Иногда многоугольник определяется как замкнутая область плоскости ограниченная замкнутой ломаной без самопересечений. Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника. Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями.

МНОГОУГОЛЬНИК a – сторона правильного многоугольникаA, B, C, D, E, F – вершины многоугольника  Площадь правильного многоугольника (S) равна: S= r·p=1/2r·n·a