Презентация на тему: Элементы планиметрии

Элементы планиметрии Планиметрия – это от латинского planum — «плоскость»,  от древне-греческого μετρεω — «измеряю» раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры (т.е. фигуры, которые можно расположить в пределах одной плоскости). В5 В8 В этой теме мы рассмотрим задачи на вычисление площадей фигур, а также задачи на вычисление величин углов или длин отрезков. Среди традиционных геометрических задач, значительное количество вопросов мы уделим на определение характеристик геометрических фигур, нарисованных на клетчатой бумаге с квадратными клетками. Как правило, это простые, хотя иногда и непривычные задачи. Значительный процент задач связан с применением тригонометрии для решения геометрических задач. Поэтому особое внимание мы уделим повторению соответствующих формул.

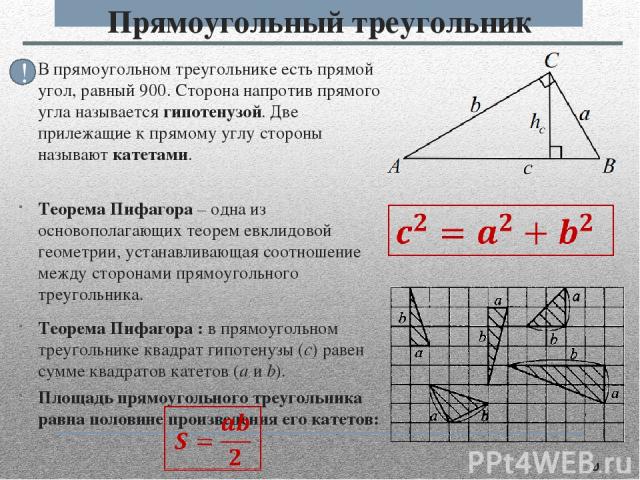
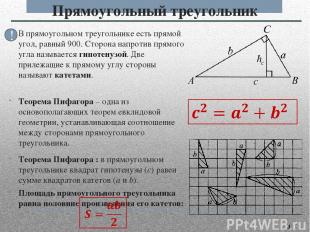
В прямоугольном треугольнике есть прямой угол, равный 900. Сторона напротив прямого угла называется гипотенузой. Две прилежащие к прямому углу стороны называют катетами. Теорема Пифагора – одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Теорема Пифагора : в прямоугольном треугольнике квадрат гипотенузы (с) равен сумме квадратов катетов (a и b). Площадь прямоугольного треугольника равна половине произведения его катетов: Прямоугольный треугольник !

Площадь плоской фигуры – это аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. Аддитивность (от латинского additivus – прибавляемый) – свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме объемов составляющих его частей. Аддитивность площади означает, что площадь фигуры равна сумме площадей её частей, если этих частей конечное число. Площади плоских фигур

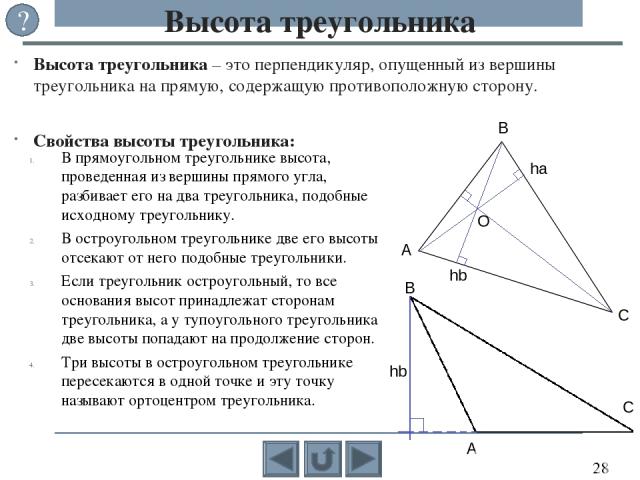
Медиана треугольника (от лат. mediana – «средняя») – это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Свойства медианы треугольника: Медиана треугольника Медиана разбивает треугольник на два треугольника одинаковой площади. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников. ? A B C O mc mb ma Для построения медианы необходимо выполнить следующие действия: найти середину стороны; соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком. Свойства медианы треугольника: Медиана разбивает треугольник на два треугольника одинаковой площади. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

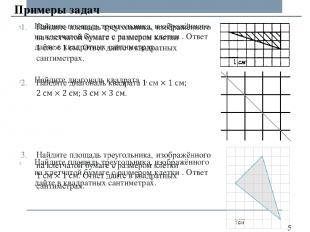
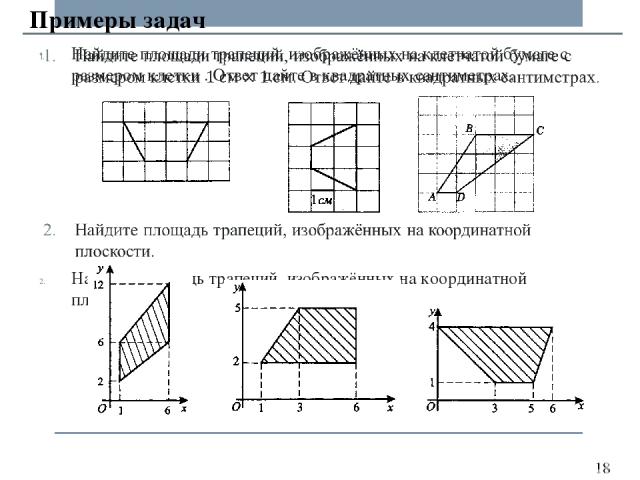
Примеры задач

Любая точка на координатной плоскости характеризуется двумя числами – координатами: абсциссой и ординатой. Если у двух точек одинаковые абсциссы или одинаковые ординаты, то соответствующие отрезки параллельны осям координат. В таких случаях длину отрезка можно найти, если вычесть различающиеся координаты точек. Прямоугольный треугольник А(4;10), В(4; 2), С(6;2)

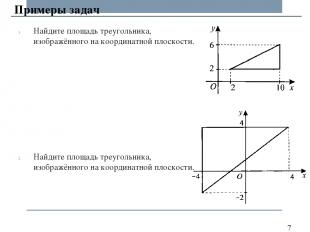
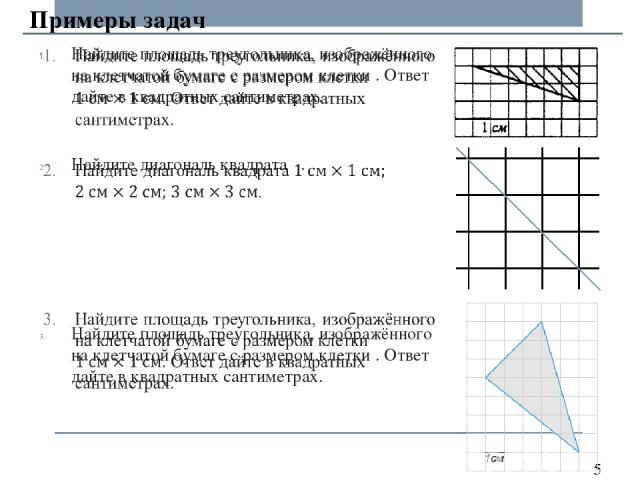
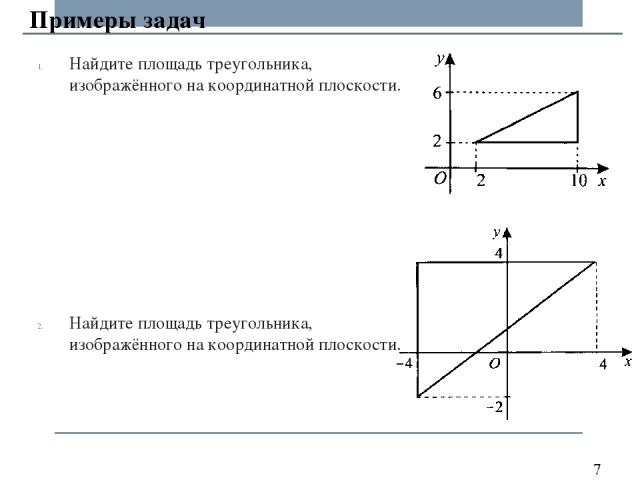
Найдите площадь треугольника, изображённого на координатной плоскости. Найдите площадь треугольника, изображённого на координатной плоскости. Примеры задач

Площадь произвольного треугольника равна половине произведения длины его стороны (a) на высоту (h), проведенную к этой стороне: Как правило, в качестве высоты и основания удобно брать те стороны, которые проходят по линиям клеточной бумаги (или же проходит параллельно осям координат). Площадь произвольного треугольника

Треугольник называют прямоугольным, если у него есть прямой угол. Свойства прямоугольного треугольника: Прямоугольный треугольник Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой. По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы). Сумма двух острых углов прямоугольного треугольника равна прямому углу. Две высоты прямоугольного треугольника совпадают с его катетами. Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы. Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности. ?

Прямоугольник – четырёхугольник, у которого все углы прямые (равны 90 градусам). Противоположные стороны прямоугольника попарно равны. Площадь прямоугольника (квадрата) Площадь прямоугольника равна произведению его смежных сторон: Прямоугольник, все стороны которого равны, называется квадратом. Площадь квадрата равна квадрату его стороны: ! ! A B C D a b

Примеры задач

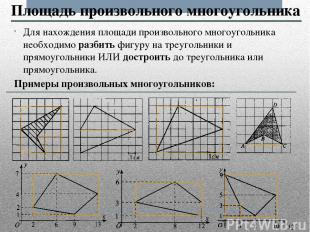
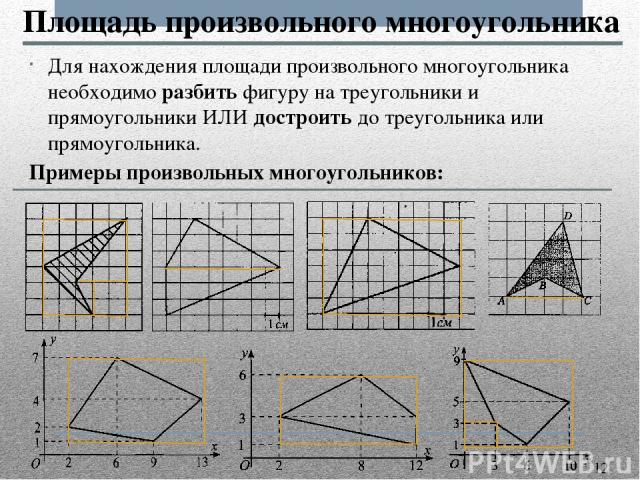
Для нахождения площади произвольного многоугольника необходимо разбить фигуру на треугольники и прямоугольники ИЛИ достроить до треугольника или прямоугольника. Примеры произвольных многоугольников: Площадь произвольного многоугольника

Ромб – это четырехугольник, у которого все стороны равны. В ромбе диагонали взаимно перпендикулярны и делятся пополам точкой пересечения. Площадь ромба Площадь ромба равна половине произведения его диагоналей: Квадрат является ромбом. Ромб является параллелограммом и обладает его свойствами. ! ! a

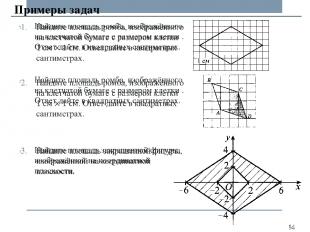
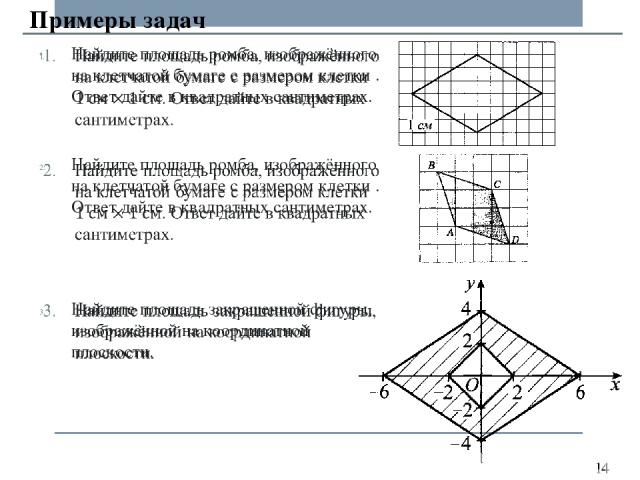
Примеры задач

Свойства параллелограмма: Противоположные стороны попарно равны и параллельны. Противоположные углы попарно равны. Диагонали пересекаются и точкой пересечения делятся пополам. Площадь параллелограмма равна произведению длины его стороны (a) на высоту (h), проведённую к этой стороне: Прямоугольник, квадрат, ромб – это четырехугольники, которые являются параллелограммом. Они обладают свойствами параллелограмма. Площадь параллелограмма Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны, т.е. лежат на параллельных прямых. ! a h

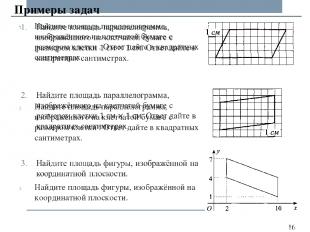
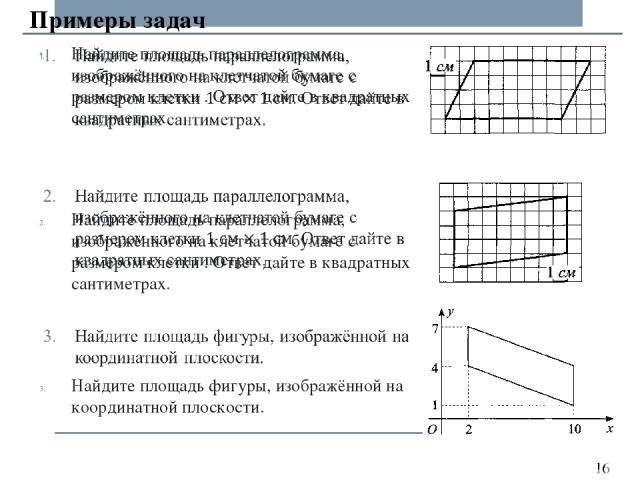
Примеры задач

Площадь трапеции a h Трапеция – четырёхугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные – боковыми сторонами. b Площадь трапеции равна половине произведения суммы оснований (a + b) на высоту (h):

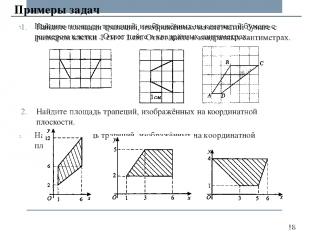
Примеры задач

Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круга — О) на расстояние, не превышающее заданное (радиус круга). Площадь круга равна произведению числа π на квадрат радиуса: Площадь круга А А

Примеры задач

Площадь кругового сектора

Примеры задач

Элементы планиметрии Координаты и векторы В5 В8 В этой теме мы рассмотрим задачи на вычисление площадей фигур, а также задачи на вычисление величин углов или длин отрезков. Среди традиционных геометрических задач, значительное количество вопросов мы уделим на определение характеристик геометрических фигур, нарисованных на клетчатой бумаге с квадратными клетками. Как правило, это простые, хотя иногда и непривычные задачи. Значительный процент задач связан с применением тригонометрии для решения геометрических задач. Поэтому особое внимание мы уделим повторению соответствующих формул.

Координаты точек Расстояние между точками A(xA, yA) и B(xB,yB): Середина C отрезка AB, где A(xA, yA) и B(xB,yB): B(хB;уB)

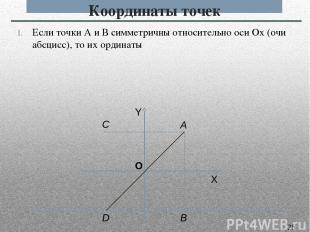
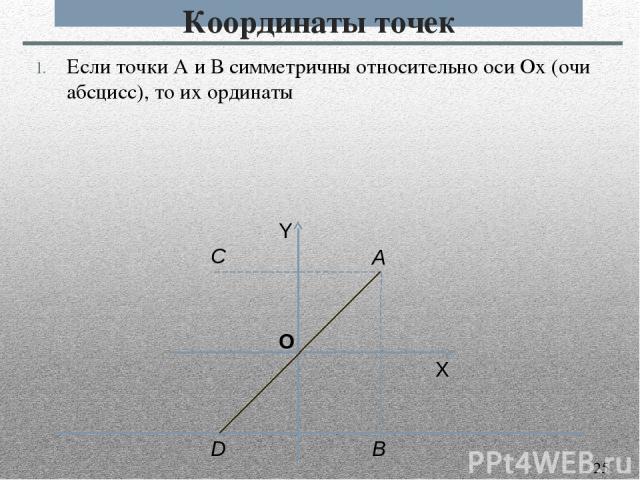
Координаты точек Если точки А и В симметричны относительно оси Ох (очи абсцисс), то их ординаты

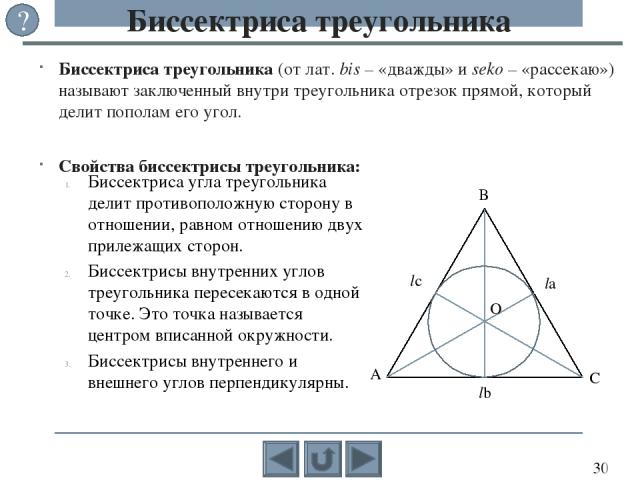
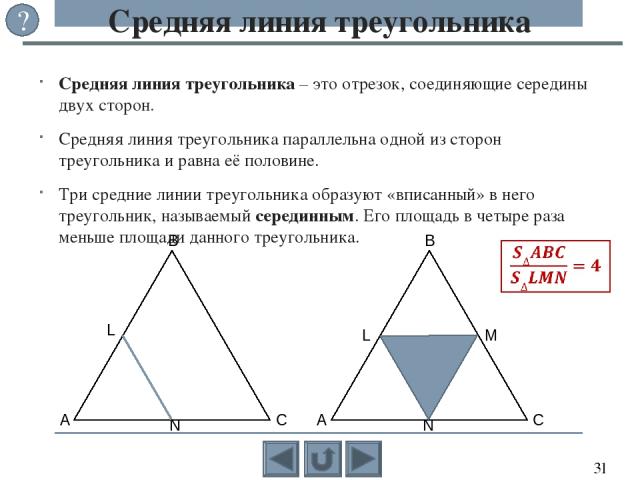
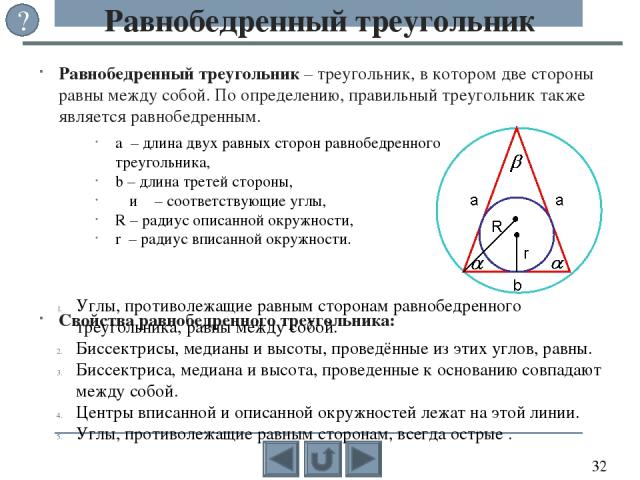
Треуго льник – многоугольник с тремя сторонами, или замкнутая ломаная, состоящая из трёх звеньев. Угол, образованный сторонами треугольника и лежащий в его внутренней области, называется внутренним углом, а смежный к нему является смежным углом треугольника. Треугольник Основные элементы треугольника ABC: Вершины – точки A, B, и C; Стороны – отрезки a = BC, b = AC и c = AB, соединяющие вершины; Углы – α , β, γ образованные тремя парами сторон. Углы часто обозначают так же, как и вершины, – буквами A, B и C. ?

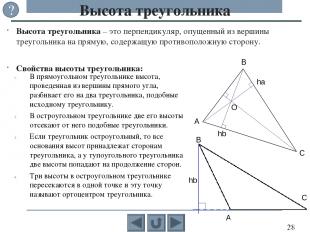
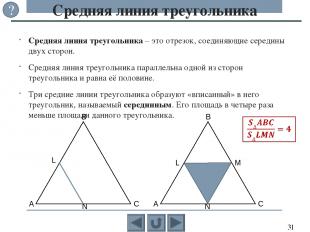
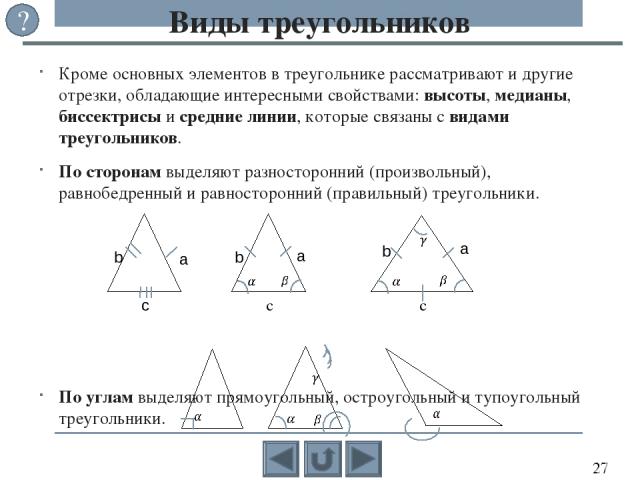
Кроме основных элементов в треугольнике рассматривают и другие отрезки, обладающие интересными свойствами: высоты, медианы, биссектрисы и средние линии, которые связаны с видами треугольников. По сторонам выделяют разносторонний (произвольный), равнобедренный и равносторонний (правильный) треугольники. По углам выделяют прямоугольный, остроугольный и тупоугольный треугольники. Виды треугольников c c ? b a b a c b a